Kontynuując cykl o Pipelines w SciKit-Learn zajmiemy się tematem kręcenia śrubkami w modelach w poszukiwaniu najlepszego wyniku. Użyjemy do tego pakietu hyperopt.
W poprzednich częściach poznawaliśmy co to "pipeline" w SciKit-Learn, tworzyliśmy własne estymatory (przy okazji ucząc się trochę o programowaniu obiektowym, klasach i dziedziczeniu – nawet jeśli to było nieświadome). Dzisiaj ostatnia część z cyklu – kręcenie śrubkami zwanymi hyperparametrami.

Ostatnio przeszukiwaliśmy siatkę hyperparametrów (wszystkie możliwe kombinacje) przy użyciu wbudowanych w SciKit-Learn mechanizmów (na przykład GridSearchCV). Dzisiaj poszukamy innej metody, innego pakietu. A będzie nim hyperopt.
Co to jest?
Zaczniemy od tego dlaczego hyperopt a nie GridSearch? Ano dlatego, że pakiet hyperopt posiada kilka funkcji, które pozwalają na zdefiniowanie przestrzeni parametrów (czyli elementów na siatce) w sposób w którym nie musimy podawać każdej z wartości (jako np. listę) a możemy użyć funkcji generujących rozkład wartości dla każdego z parametrów. Później określamy np. ile czasu ma trwać szukanie najlepszej kombinacji (albo ile kroków) i pakiet za nas dobiera najlepsze kombinacje. Oczywiście dobór odbywa się na podstawie szukania najmniejszej wartości błędu (najmniejszej straty), a nad tym co jest stratą mamy kontrolę. Może ten opis jest zagmatwany, dlatego dłuższy ale prosty przykład.
Oczywiście zaczynamy od importu pakietów i małej konfiguracji:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
from hyperopt import hp, fmin, tpe, STATUS_OK, space_eval from hyperopt import Trials import pandas as pd import numpy as np import pprint import seaborn as sns import matplotlib.pyplot as plt sns.set_theme(style="darkgrid") pp = pprint.PrettyPrinter(width=60, compact=True) |
Będziemy szukać współrzędnej X wierzchołka paraboli. Bo to taka funkcja, która ma jedno konkretne minimum (lub maksimum) i dość łatwo na tym przykładzie zrozumieć ideę działania samego hyperopt ale też funkcji straty.
|
1 2 3 4 5 6 |
# definiujemy sobie funkcję obliczającą wartość Y w konkretnym punkcie X def parabola(x, pa, pb, pc): return pa * x**2 + pb * x + pc # parablolę opisują 3 wskaźniki, niech będą takie: a, b, c = (-2, 8, -4) |
Na początek zobaczmy jak nasza parabola wygląda:
|
1 2 3 4 |
x = np.arange(-100, 100) y = parabola(x, a, b, c) sns.scatterplot(x=x, y=y) |
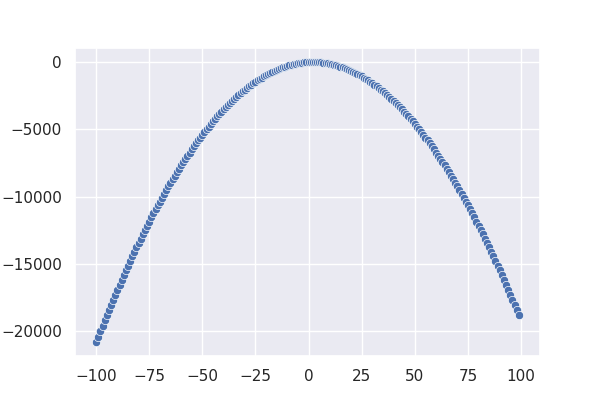
Mamy więc wypukłą ku górze krzywą, będziemy szukać punktu najwyżej położonego. Ten punkt ma wartość:
|
1 2 3 4 |
y_max = np.max(y) y_max ## 4 |
a przyjmuje ją dla argumentu:
|
1 2 3 |
x[np.argmax(y)] ## 2 |
Oczywiście można to policzyć matematycznie, ale… nie pamiętam wzoru na wierzchołek paraboli, a wyprowadzać tego poprzez szukanie miejsca zerowego pierwszej pochodnej mi się nie chce.
Będziemy szukać takiej wartości argumentu funkcji straty aby owa strata była jak najmniejsza. Czyli odległość (w sensie wartości funkcji, Y) od naszego wierzchołka paraboli musi być najmniejsza. Przygotujmy więc odpowiednią funkcję straty:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
def funkcja_straty(args): # hyperopt przekazuje słownik parametrów - wyciągamy z niego nasz X x = args['x'] # obliczamy Y na naszzej paraboli (a, b i c są stałe) y = parabola(x, a, b, c) # do hyperopt zwracamy słownik: # - status (udało się) # - opcjonalnie zwracamy jakieś inne argumenty # - koniecznie wartość straty return {'loss': abs(y_max-y), 'status': STATUS_OK, 'type': args['type']} |
Jak wspomniałem wyżej – stratą jest odległość od wierzchołka i chcemy aby była (idealnie) równa zero. Stąd absolutna wartość powyżej w elemencie loss.
Teraz zdefiniujemy sobie przestrzeń parametrów w jakich będziemy szukać naszego idealnego X. Tutaj pojedziemy od razu po bandzie i powiemy, że mamy 3 warianty budowania wartości X:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
parabola_space = hp.choice('wiercholek_x', [ { 'type': 'x_normal', 'x': hp.normal('x_normal', 0, 300) # rozkład normalny o średniej 0 i odychleniu 300 }, { 'type': 'x_randint', 'x': hp.randint('x_randint', -1000, 1000) # losowa liczba całkowita z przedziału -1000 ; 1000 }, { 'type': 'x_uniform', 'x': hp.uniform('x_uniform', -1000, 1000) # rozkład jednorodny z przedziału -1000 ; 1000 } ]) |
Czas na najważniejszą część. Wywołujemy szukanie minimum funkcji straty. Tutaj mówimy, że nie więcej niż 1000 kroków, korzystają z przestrzeni parametrów jak wyżej (wybór jednego z trzech typów rozkładów i w ramach niego jakiejś liczby), a wybór odpowiednich parametrów zostawiamy algorytmowi (tpe.suggest):
|
1 2 3 |
best = fmin(funkcja_straty, parabola_space, algo=tpe.suggest, max_evals=1000) ## 100%|##########| 1000/1000 [00:17<00:00, 57.95trial/s, best loss: 5.2314085588811565e-05] |
Chwilę to trwa i dostajemy najlepszy wynik:
|
1 2 3 |
best ## {'wiercholek_x': 0, 'x_normal': 1.9948856043568748} |
Jak to czytać? Najlepiej sprawdził się zerowy element tablicy wyboru rozkładów (a więc rozkład x_normal) i wartość x w okolicach dwójki. Oczywiście rozkłady są losowe, więc za każdym razem może wyjść nieco inna liczba. Przy zwiększeniu liczby kroków do np. 10 tysięcy dostaniemy lepszą precyzję (testując w okolicach 3 tysięcy kroków miałem dokładność na poziomie 2e-5, po 10 tysiącach strata była na poziomie 7e-7).
No dobrze, ale to jest najlepszy wynik (co może być wystarczające) będący najlepszą kombinacją hyperparametrów (tutaj jednego – wartości X). A może chcemy znać całą historię szukania, ze wszystkimi kombinacjami? Tutaj wchodzi zapisywanie kolejnych prób i obiekty typu "Trials". Zmiana jest minimalna – tworzymy obiekt, a później podajemy go do fmin():
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
trials = Trials() # usuwamy rozkład normalny - bez niego łatwiej będzie coś zaobserwować parabola_space_v2 = hp.choice('wiercholek_x', [ { 'type': 'x_randint', 'x': hp.randint('x_randint', -1000, 1000) # losowa liczba całkowita z przedziału -1000 ; 1000 }, { 'type': 'x_uniform', 'x': hp.uniform('x_uniform', -1000, 1000) # rozkład jednorodny z przedziału -1000 ; 1000 } ]) best = fmin(funkcja_straty, parabola_space_v2, algo=tpe.suggest, max_evals=500, trials=trials) ## 100%|##########| 500/500 [00:05<00:00, 89.20trial/s, best loss: 0.22263845159594542] |
Teraz każdy przebieg mamy zapisany w pamięci i możemy to wykorzystać. Na przykład najlepszy wynik dało:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
pp.pprint(trials.best_trial) ## {'book_time': datetime.datetime(2020, 12, 23, 12, 9, 33, 709000), ## 'exp_key': None, ## 'misc': {'cmd': ('domain_attachment', 'FMinIter_Domain'), ## 'idxs': {'wiercholek_x': [374], ## 'x_randint': [], ## 'x_uniform': [374]}, ## 'tid': 374, ## 'vals': {'wiercholek_x': [1], ## 'x_randint': [], ## 'x_uniform': [1.666354640676702]}, ## 'workdir': None}, ## 'owner': None, ## 'refresh_time': datetime.datetime(2020, 12, 23, 12, 9, 33, 709000), ## 'result': {'loss': 0.22263845159594542, ## 'status': 'ok', ## 'type': 'x_uniform'}, ## 'spec': None, ## 'state': 2, ## 'tid': 374, ## 'version': 0} |
Co tutaj widać:
- strata w ramach result / loss
- użyte parametry w vals (nazwa użyta do oznaczenia rozkładu i wartość jaką przyjął X)
Zwróć uwagę, że tutaj było mniej przebiegów, zatem i błąd większy (nie zdążyła znaleźć się ta najlepsza wartość).
Wyniki mamy w formie listy zagnieżdżonych obiektów. Możemy z tego powyjmować interesujące elementy do tabeli i przygotować jakieś zestawienia.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
trials_df = [] for trial in trials.trials: trials_df.append({ 'loss': trial['result']['loss'], 'type': trial['result']['type'], 'x': trial['misc']['vals'][trial['result']['type']][0] }) trials_df = pd.DataFrame(trials_df) trials_df['index'] = trials_df.index trials_df.head() ## loss type x index ## 0 4.380480e+05 x_randint -466.000000 0 ## 1 8.307353e+04 x_uniform -201.805704 1 ## 2 1.042079e+06 x_uniform 723.830663 2 ## 3 4.050000e+03 x_randint 47.000000 3 ## 4 2.643303e+03 x_uniform -34.354527 4 |
Zobaczmy czy każdy z typów rozkładów był użyty tyle samo razy (czyli czy algorytm rozłożył sobie wszystkie możliwe parametry w siatkę i przeszedł ją jakoś równo, czy używając już zdobytych informacji o stracie optymalizował drogę?
|
1 2 3 4 5 6 |
trials_df.value_counts('type', ascending=False) ## type ## x_uniform 379 ## x_randint 121 ## dtype: int64 |
Jak widać nie każdy z rozkładów użyty był tak samo często. Zobaczmy na wykresie jakie X były losowane i jaką dawały stratę:
|
1 2 |
m = sns.FacetGrid(data=trials_df, col='type', height=5) m.map(sns.scatterplot, 'x', 'loss') |
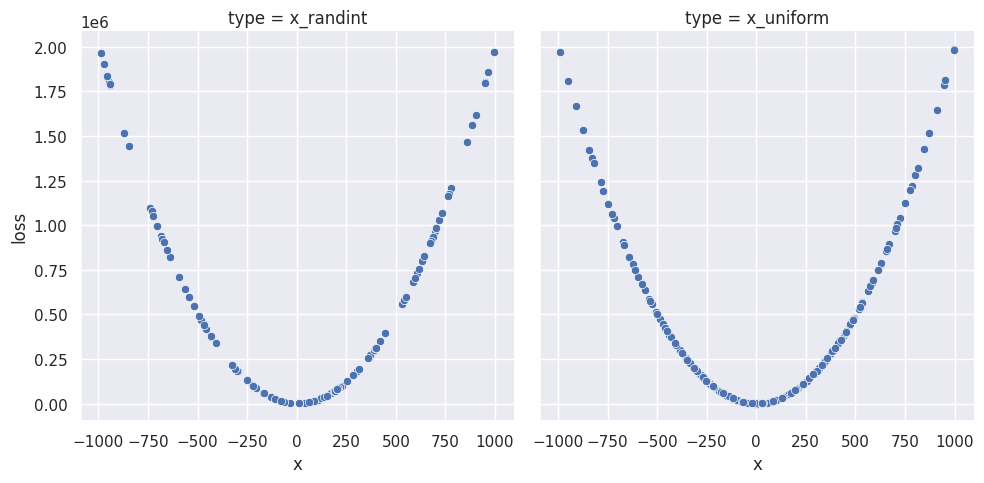
Wygląda z grubsza, że każda z liczby X była losowana mniej więcej tyle samo razy. Ale ten wykres jest mylący – trzeba to zweryfikować inaczej:
|
1 |
sns.displot(trials_df.x, kind = "kde") |
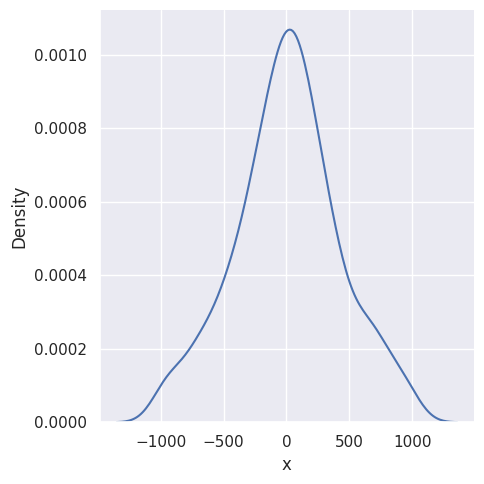
Mamy szeroki zakres (łącznie przestrzeń szerokości 2000 jednostek), losowany na dwa sposoby z rozkładem jednostajnym (właściwie dwoma) – więc każda z liczb powinna być tak samo prawdopodobna do wylosowania. Ale wynik pokazuje zbliżanie się do rozkładu normalnego (przechodząc proces 10 tysięcy razy widać to jeszcze lepiej – średnia zbliża się do naszej dwójki, a odchylenie standardowe maleje tak, że mamy właściwe szpilkę a nie dzwon). W sumie może Wam się udać to wcześniej – jeśli z randint wylosuje się dwójka to od razu jesteśmy w domu, bo strata ma wartość zerową.
Sprawdźmy czy im bliżej końca przebiegu osiągamy coraz lepsze wyniki (coraz mniejsza strata). Tutaj mamy sporą losowość, więc może być różnie.
|
1 |
sns.scatterplot(data=trials_df, x='index', y='loss', hue='type') |
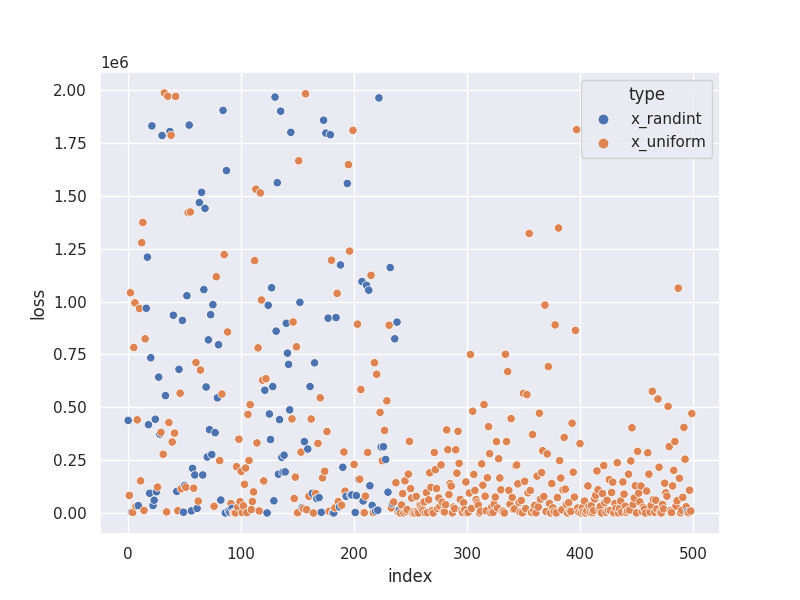
Tyle wprowadzenia do hyperopt. To jest początek, ale pokrywający spory kawałek możliwości hyperopt. Więcej oczywiście w dokumentacji.
Jak tego użyć?
Najbardziej sensownym i pewnie też najpopularniejszym użyciem jest szukanie najlepszego modelu i kręcenie śrubkami jego hyperparametrów. Zróbmy tak:
- przygotujemy jakieś sztuczne dane na potrzeby klasyfikacji
- przygotujmy szkielet – pipeline
- przygotujmy listę klas modeli (różne ich typy) razem z zakresem hyperparametrów jakimi można kręcić dla każdego z nich
- wytrenujmy i oceńmy każdą kombinację
- w wyniku dostaniemy najlepszą wersję (a w gratisie kilka cennych danych poszerzających wiedzę o tym jak hyperparametry wpływają na dany typ modelu)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
from sklearn.pipeline import Pipeline # ocena modelu from sklearn.model_selection import cross_val_score # nasze modele klasyfikacyjne from sklearn.ensemble import RandomForestClassifier, AdaBoostClassifier from sklearn.svm import SVC from sklearn.neighbors import KNeighborsClassifier from xgboost import XGBClassifier # narzędzie do preparowania danych from sklearn.datasets import make_classification |
Przygotujemy dane. Wiele razy w takim przypadku szukałem jakiegoś zbioru, a przecież SciKit-Learn ma to tego znakomite funkcje w module datasets:
|
1 |
data = make_classification(n_samples=1000, n_classes=4, n_features=20, n_informative=16) |
Trochę sobie te dane uporządkujemy – po prostu wpakujemy w data frame:
|
1 2 3 |
X = pd.DataFrame(data[0]) X.columns = [f"col_{i}" for i in X.columns] y = data[1] |
Czas na przygotowanie klasyfikatorów i zakresu zmian ich hyperparametrów.
Właśnie przeczytałem świetną książkę (dla średnio zaawansowanych pythonowców idealna) "Python. Dobre praktyki profesjonalistów" autorstwa Dane Hillard więc przekazuję odrobinę zdobytej wiedzy – można konfigurację każdego z klasyfikatorów ubrać w element typu dict, a potem w jednej pętli przejść przez wszystkie. Poniżej 5 konfiguracji (lista 5 elementów typu słownik) dla 5 różnych klasyfikatorów:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
classifiers = [ { 'name': 'RandomForestClassifier()', 'class': RandomForestClassifier(), 'max_evals': 50, 'params': { 'n_estimators': hp.uniformint('n_estimators', 10, 250), 'max_depth': hp.uniformint('max_depth', 2, 20) } }, { 'name': 'KNeighborsClassifier()', 'max_evals': 20, 'class': KNeighborsClassifier(), 'params': { 'n_neighbors': hp.uniformint('n_neighbors', 1, 10), 'p': hp.choice('p', [1, 2]) } }, { 'name': 'SVC()', 'class': SVC(), 'max_evals': 4, 'params': { 'kernel': hp.choice('kernel', ['linear', 'poly', 'rbf', 'sigmoid']) } }, { 'name': 'AdaBoostClassifier()', 'class': AdaBoostClassifier(), 'max_evals': 20, 'params': { 'n_estimators': hp.uniformint('n_estimators', 10, 250), 'learning_rate': hp.uniform('lr', 0.01, 0.05) } }, { 'name': 'XGBClassifier()', 'class': XGBClassifier(), 'max_evals': 100, 'params' : { 'learning_rate': hp.loguniform ('learning_rate', 0.01, 0.5), 'max_depth': hp.choice('max_depth', np.arange(2, 11).tolist()), 'min_child_weight': hp.choice('min_child_weight', np.arange(0, 101).tolist()), 'gamma': hp.loguniform('gamma', 0.0, 2.0), 'subsample': hp.uniform('subsample', 0.5, 1.0), 'colsample_bytree': hp.uniform('colsample_bytree', 0.5, 1.0), 'colsample_bylevel': hp.uniform('colsample_bylevel', 0.5, 1.0), 'reg_alpha': hp.loguniform('reg_alpha', 0.0, 2.0), 'reg_lambda': hp.loguniform('reg_lambda', 0.0, 2.0) } } ] |
Jednak aby hyperopt mógł dać jakiś wynik potrzebujemy funkcji straty. Oto i ona (wraz z odpowiednim komentarzem):
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
def objective(space): # miejsce na parametry dla Pipeline pipe_params = {} # przechodzimy przez listę parametrów dla estymatora i budujemy ich słownik for s in space: pipe_params[f"classifier__{s}"] = space[s] # dostrajamy Pipeline - podajemy mu zebrane parametry pipeline.set_params(**pipe_params) # oceniamy model - używamy cross-validacji i wyciągamy średnią z "accuracy" dla 10 przebiegów score = cross_val_score(pipeline, X, y, cv=10, scoring="accuracy").mean() # im większe "accuracy" tym lepiej - zatem strata to 1-accuracy (max accuracy to 1) # przy okazji do traials zwracamy też "czyste" accuracy return {'loss': 1- score, 'status': STATUS_OK, 'accuracy': score} |
Teraz kiedy wszystko przygotowane możemy puścić pętlę przez wszystkie zdefiniowane wcześniej klasyfikatory (razem z ich przestrzenią hyperparametrów). Dla każdego z klasyfikatorów poniższy kod:
- przygotuje pusty pipeline
- przygotuje przestrzeń hyperparametrów space
- znajdzie najlepszą konfigurację i ją wyświetli
- a wszystkie przejścia dla wszystkich modeli dopisze do listy trials_df
Całość trochę trwa (u mnie na maszynie 8 CPU @ 16 GB RAM jakieś 30 minut; maszynę VPS mam z webh.pl, chwalę sobie), więc możesz uruchomić kod i iść na przykład na kawę:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 |
trials_df = [] for cl in classifiers: cl_name = cl['class'].__class__.__name__ print(f"\n\n{cl_name}") pipeline = Pipeline(steps=[('classifier', cl['class'])]) space = {} for k in cl['params']: space[k] = cl['params'][k] max_evals = cl['max_evals'] trials = Trials() best = fmin(fn=objective, space=space, algo=tpe.suggest, max_evals=max_evals, trials=trials) best_params = space_eval(space, best) print('\nThe best params:') print ("{:<30} {}".format('Parameter','Selected')) for k, v in best_params.items(): print ("{:<30} {}".format(k, v)) for trial in trials.trials: trials_df.append({ 'classifier': cl_name, 'loss': trial['result']['loss'], 'accuracy': trial['result']['accuracy'], 'params': trial['misc']['vals'] }) RandomForestClassifier The best params: Parameter Selected max_depth 11 n_estimators 201 KNeighborsClassifier The best params: Parameter Selected n_neighbors 9 p 2 SVC The best params: Parameter Selected kernel poly AdaBoostClassifier The best params: Parameter Selected learning_rate 0.04875201977122034 n_estimators 218 XGBClassifier The best params: Parameter Selected colsample_bylevel 0.9202731839690937 colsample_bytree 0.7877034902279985 gamma 1.520140728607678 learning_rate 1.4043916957633775 max_depth 3 min_child_weight 7 reg_alpha 1.2521512808123185 reg_lambda 1.6803809580682991 subsample 0.7179791178304575 |
Zebrane wyniki (trials_df) mamy w postaci listy słowników, więc przekształćmy ją w zwykły pandasowy data frame:
|
1 |
trials_df = pd.DataFrame(trials_df) |
Teraz możemy porównać wyniki i same modele ze sobą. W klasyfikacji interesuje nam accuracy więc to sobie zobaczmy:
|
1 |
sns.swarmplot(data=trials_df, y='classifier', x='accuracy') |
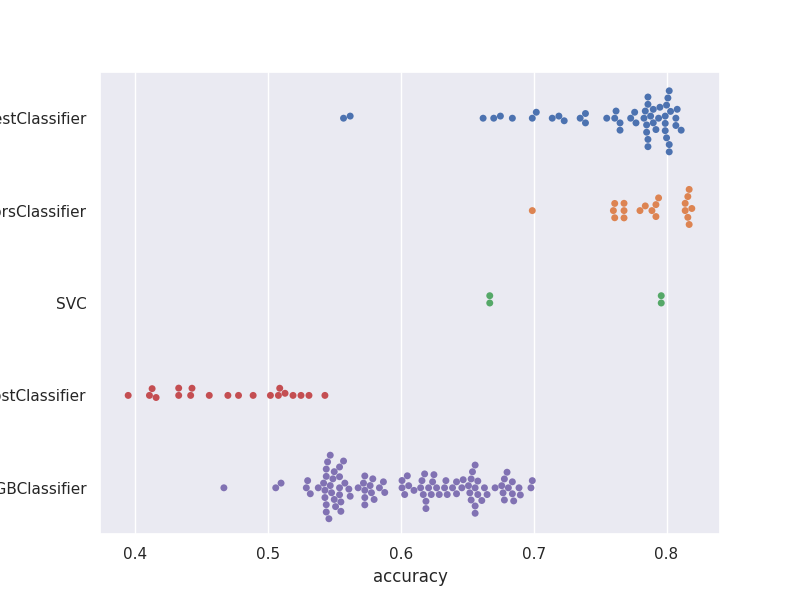
Widzimy tutaj, że każdy z klasyfikatorów był testowany różną ilość razy (różna liczba kropek) – ale to oczywiście zależy od wartości "max_evals" jaką przypisaliśmy w konfiguracji.
Możemy wybrać jeden z klasyfikatorów (na przykład XGBoost – miał najwięcej parametrów i najbardziej był męczony) i sprawdzić jak ma się accuracy w zależności od wartości poszczególnych hyperparametrów:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# wybieramy tylko wyniki dla klasyfikatora XGBoost xgb_trails = trials_df[trials_df['classifier'] == 'XGBClassifier'][['accuracy', 'params']] # rozszerzamy kolumnę ze słownikiem na kolumny z poszczególnych elementów słownika i pakujemy w jedną ramkę razem z 'accuracy' xgb_trails = pd.concat([xgb_trails[['accuracy']], xgb_trails.params.apply(pd.Series)], axis=1) # wartości dla elementów słownika zostały jako listy (jednoelementowe) - wydobywamy je poza listę for col in xgb_trails.select_dtypes(include=[list]).columns: xgb_trails[col] = xgb_trails[col].apply(lambda x: x[0]) # robimy tabelkę "tidy" na potrzebę wykresów xgb_trails_tidy = xgb_trails.melt(id_vars='accuracy', var_name='param', value_name='value') |
Oczywiście najlepiej to widać na wykresie, zatem:
|
1 2 |
m = sns.FacetGrid(xgb_trails_tidy, col='param', sharex=False, col_wrap=3) m.map(sns.scatterplot, 'value', 'accuracy') |
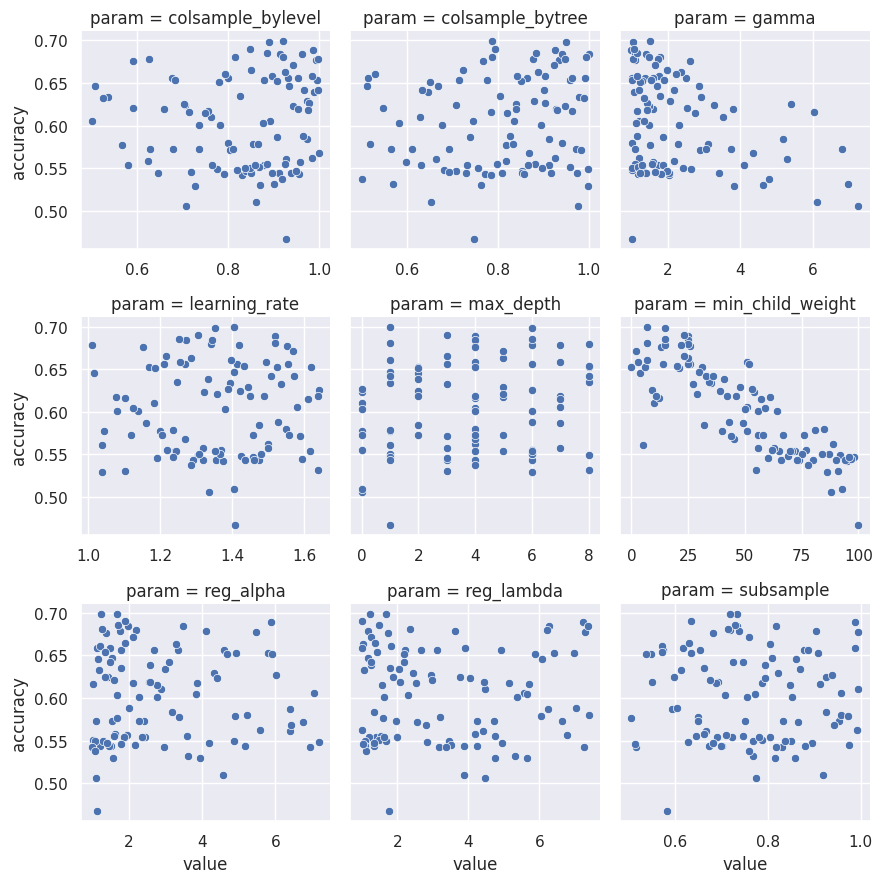
Porównajcie powyższe wykresy z tym, co hyperopt zwrócił jako najlepsze wartości wyżej:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
XGBClassifier The best params: Parameter Selected colsample_bylevel 0.9202731839690937 colsample_bytree 0.7877034902279985 gamma 1.520140728607678 learning_rate 1.4043916957633775 max_depth 3 min_child_weight 7 reg_alpha 1.2521512808123185 reg_lambda 1.6803809580682991 subsample 0.7179791178304575 |
Prawda, że spójne?
Oczywiście do pipeline można dodać transformację danych i też to przepuścić przez hyperopt – wtedy robi się kompleksowa maszyna do szukania najlepszego modelu. Warto każdy z tak wytrenowanych modeli zapisać w plikach (w ogóle warto wersjonować modele, razem z informacją o ich parametrach – poczytaj na przykład o MLFlow jeśli ten temat Cię interesuje) aby ewentualnie sprawdzić kilka wytrenowanych wersji na produkcyjnych danych. Można cały proces przygotować tak, że modele douczają się co jakiś czas, a można też tak że z użyciem hyperopt szukamy za każdym razem tego najlepszego.
Zdjęcie okładkowe to Edge2Edge Media z Unsplash