Jakie będzie bezrobocie za dwa lata?
A właściwie – jak wyznaczyć przyszłe dane na podstawie historii?
Dzisiaj zajmiemy się prostą (automatyczną) predykcją szeregów czasowych.
Co to jest szereg czasowy? Ano, zbiór danych przypisanych do kolejnych dat (chwil w czasie – będąc bardziej precyzyjnym). Może to być wartość akcji dzień po dniu, może to być temperatura (czy dowolne inne wartości opisujące pogodę) lub cokolwiek innego, co ma swoje wartości w kolejnych momentach czasu. My zajmiemy się stopą bezrobocia w Polsce.
Skorzystamy z miesięcznych danych publikowanych przez GUS. Dane są w ładnej tabelce na stronie, można więc je łatwo z niej wyciągnąć.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
library(forecast) # biblioteka do prognozowania library(dplyr) library(rvest) library(reshape2) # pobranie danych page <- read_html("http://stat.gov.pl/obszary-tematyczne/rynek-pracy/bezrobocie-rejestrowane/stopa-bezrobocia-w-latach-1990-2017,4,1.html") bezrobocie <- page %>% html_node("article") %>% html_node("section") %>% html_node("table") %>% html_table() # dla roku 2002 w tabeli mamy po dwie wartości # potrzebne jest trochę przekształceń bezrobocie[16,1] <- "2002" rownames(bezrobocie) <- bezrobocie[,1] bezrobocie <- bezrobocie[,2:13] colnames(bezrobocie) <- 1:12 for(i in 1:12) { bezrobocie[,i] <- substr(bezrobocie[,i], 1, 4) # żeby wyeliminować dwie wartości w 2002 bezrobocie[,i] <- gsub("*", "", bezrobocie[,i], fixed = TRUE) # żeby wyeliminować gwiazdki przy liczbah bezrobocie[,i] <- as.numeric(gsub(",", ".", bezrobocie[,i], fixed = TRUE)) # żeby miejsca dziesiętne były oddzielone od całości kropką a nie przecinkiem } bezrobocie$rok <- rownames(bezrobocie) # z tabeli kwadratowej przechodzimy na długą i usuwamy braki bezrobocie <- bezrobocie %>% melt() %>% na.omit() colnames(bezrobocie) <- c("rok", "miesiac", "stopa") bezrobocie <- arrange(bezrobocie, rok, miesiac) # stopa bezrobocia jako szereg czasowy bezrobocie_ts <- ts(bezrobocie$stopa, start = c(1990, 1), frequency = 12) |
Mając przygotowane dane możemy je sobie prosto narysować:
|
1 2 |
plot(bezrobocie_ts, col="black") lines(ma(bezrobocie_ts, 12), col="red") |
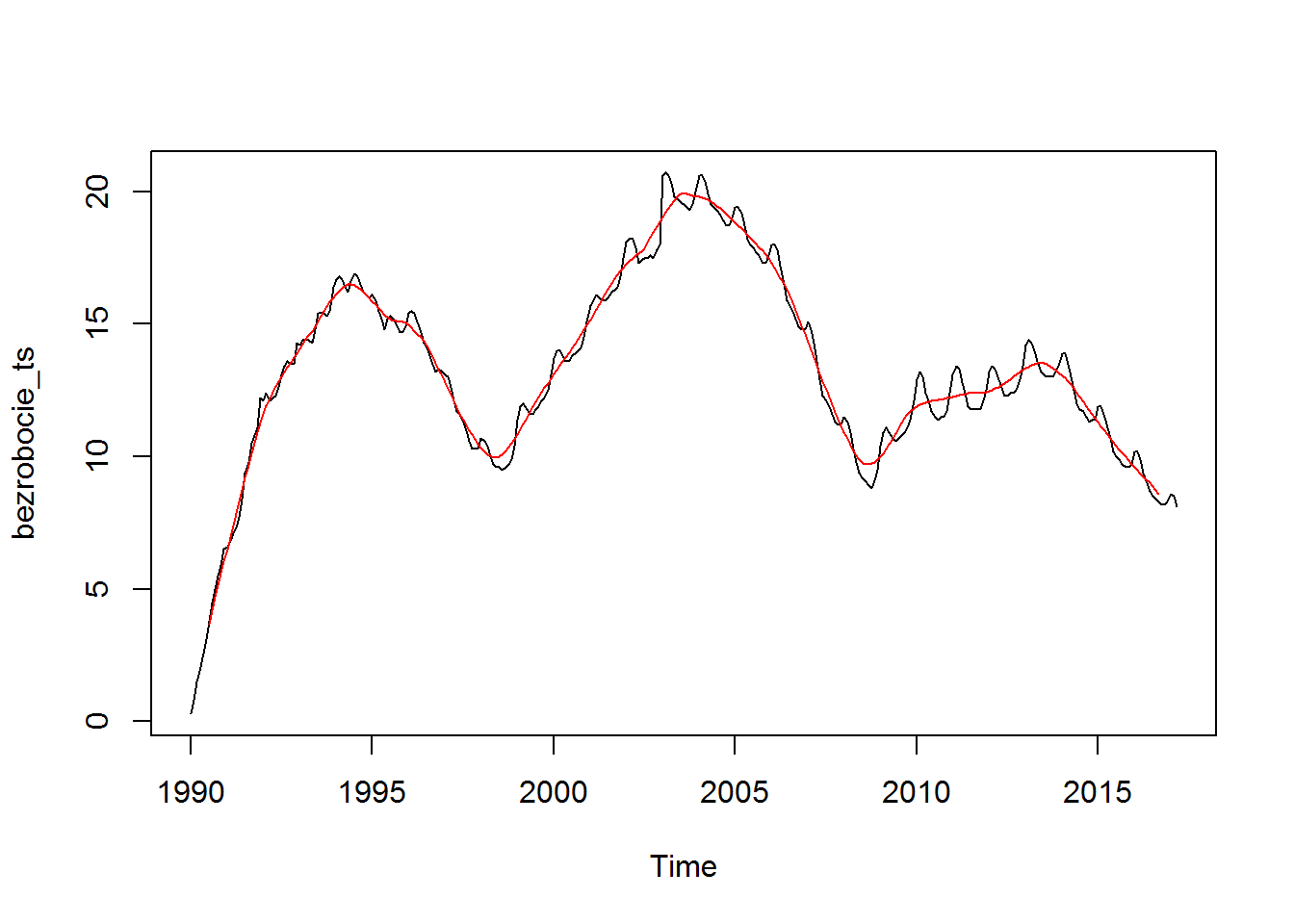
Dodałem dodatkowo czerwoną linię ze średnią ruchomą z 12-okresów.
Rozłóżmy ten szereg na składowe – zobaczymy czy jest sezonowy i jak wygląda trend:
|
1 |
plot(decompose(bezrobocie_ts)) |
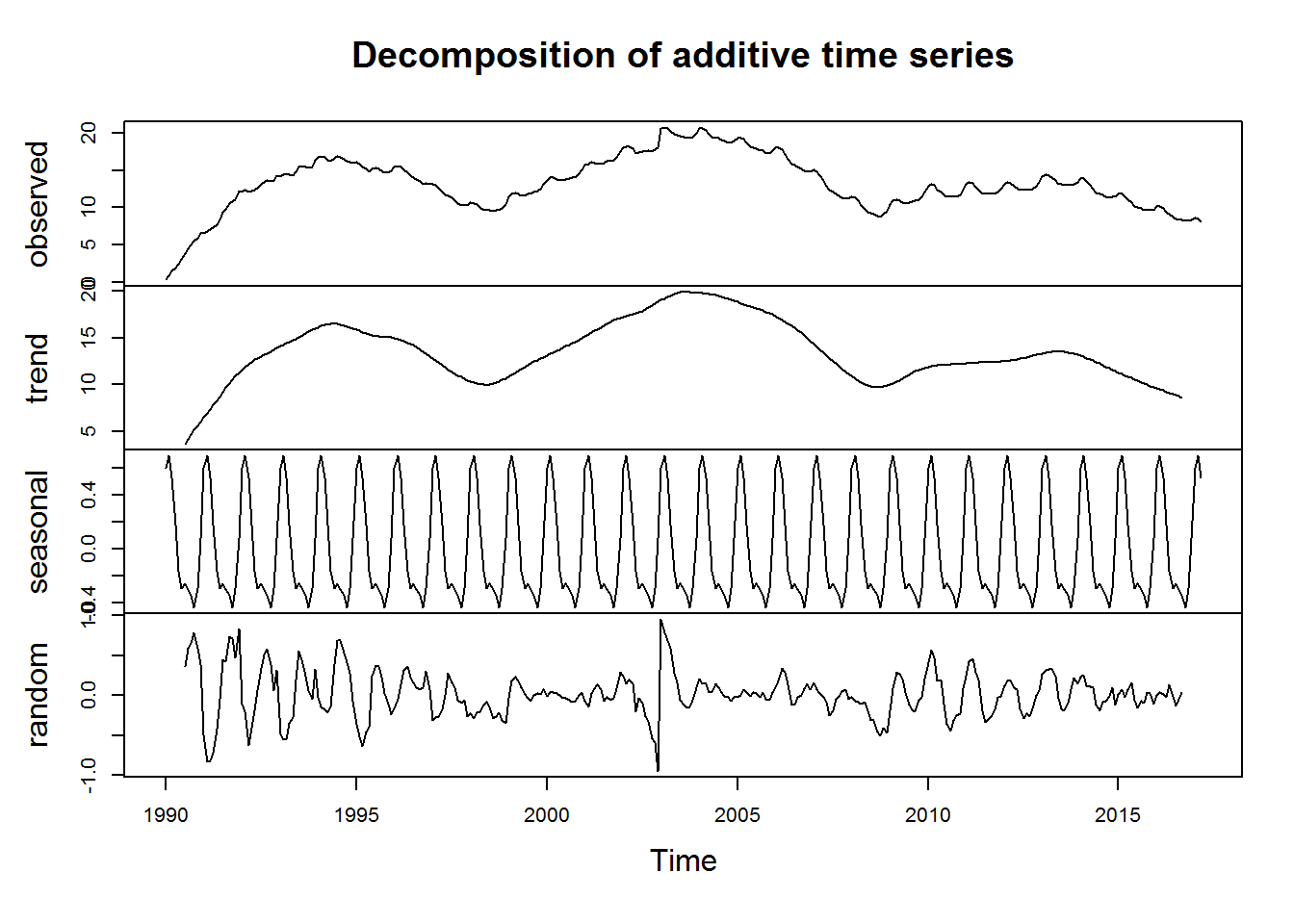
Co tutaj widać? Przede wszystkim trend jest analogiczny do ruchomej średniej narysowanej wcześniej. Ale ważniejsza jest sezonowość.
Wybierzmy kawałek danych (głównie ze względu na sporą rozpiętość stopy bezrobocia w całości danych) i zobaczmy jak to wygląda w poszczególnych miesiącach:
|
1 2 |
bezrobocie_ts_part <- window(bezrobocie_ts, start=c(2010, 1), end=c(2015, 12)) seasonplot(bezrobocie_ts_part, year.labels = TRUE, col = 1:6) |
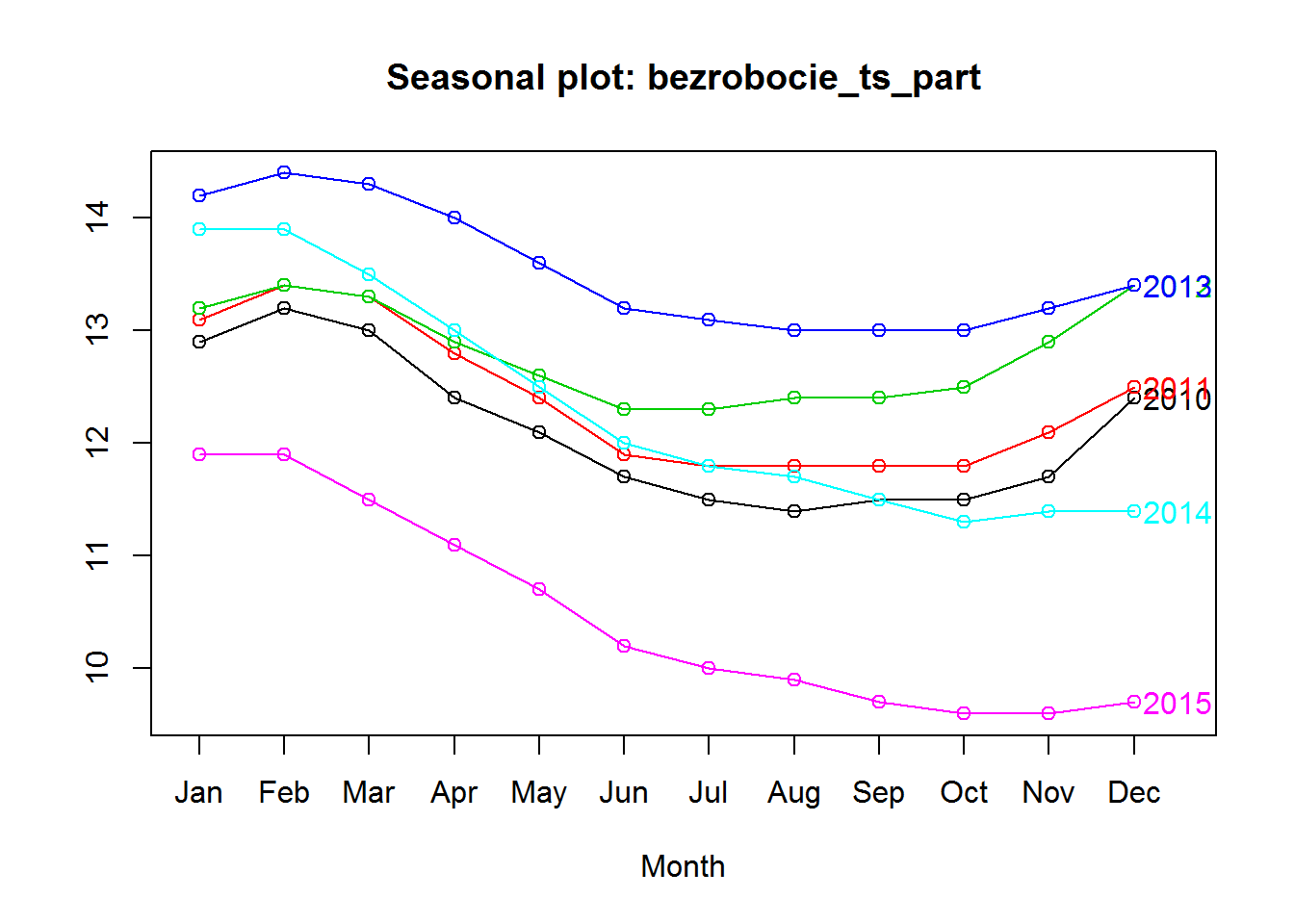
Bezrobocie jest wyraźnie sezonowe – w wakacje spada, w ciągu roku najwyższe jest w lutym/marcu. Powyższy wykres obrazuje raczej różnicę rok do roku, a tutaj
|
1 |
monthplot(bezrobocie_ts_part) |
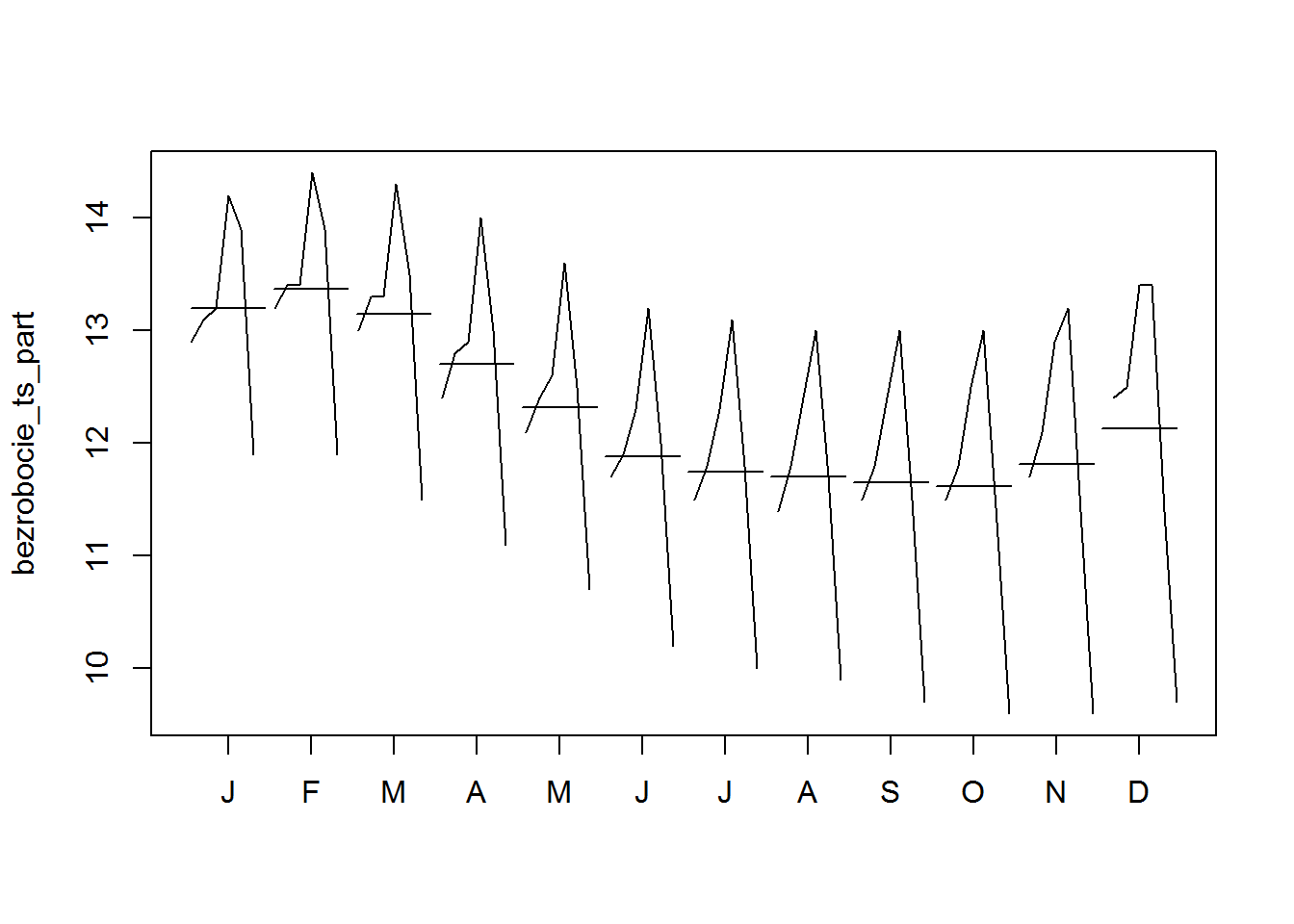
widzimy już wyraźnie różnice miesiąc do miesiąca (poziome kreski; linie to zmiana w poszczególnych miesiącach na przestrzeni lat).
Dobrze, czas na wróźenie z fusów. To znaczy z historii. Bo na tym się skupimy – nasze modele będą próbowały przewidzień przyszłość jedynie na podstawie analizy przeszłości i tego jak jest ona złożona.
Na sam początek podzielimy dane na okres treningowy (na którym zbudujemy model) i testowy (na którym sprawdzimy trafność przewidywań modelu). Za punkt rozdzielający niech posłuży koniec roku 2011.
|
1 2 |
bezrobocie_ts_learn <- window(bezrobocie_ts, end = c(2011, 12)) bezrobocie_ts_test <- window(bezrobocie_ts, start = c(2012, 1)) |
Model ARIMA
czyli Autoregressive integrated moving average – modele oparte na autoregresji średniej ruchomej. Dość dużo na ten temat można znaleźć w literaturze (ze sporą dawką matematyki), polecam też online’ową książkę. Z polskich materiałów bardzo dobrą książką prowadzącą krok po kroku w świat szeregów czasowych i ich analizy jest Analiza i prognozowanie szeregów czasowych
Bez wchodzenia w szczegóły – wykorzystamy funkcję, która wyznaczy odpowiednie współczynniki modelu samodzielnie. Czasem może się jednak okazać, że te wartości nie są zadowalające, wówczas warto poświęcić czas i spróbować wyznaczyć je samodzielnie. Jak? O tym w wymienionej literaturze.
|
1 |
bezrobocie_ts_arima <- auto.arima(bezrobocie_ts_learn) |
Mając wyznaczone współczynniki, a właściwie już cały model – zaprognozujmy wartości. Najpierw na podstawie (linijka kodu wyżej) modelu zbudowanego o dane treningowe sprawdzimy jak celne są przewidywania dla okresu danych testowych:
|
1 2 3 4 |
bezrobocie_ts_arima_forecast <- forecast(bezrobocie_ts_arima, h = length(bezrobocie_ts_test)) plot(bezrobocie_ts_arima_forecast) lines(bezrobocie_ts_test, col = "red") |
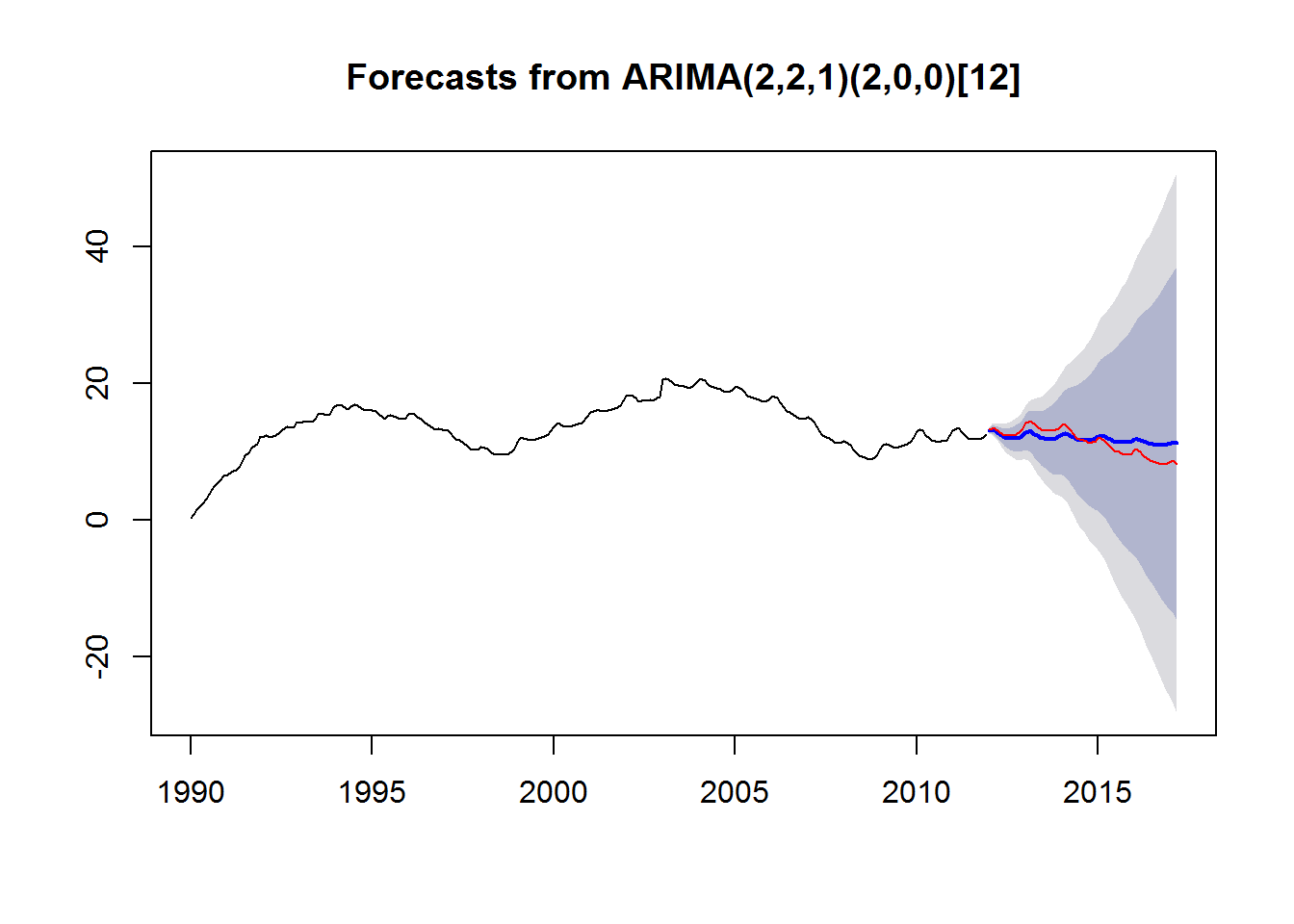
Co tutaj widać? Czarna falowana linia to dane rzeczywiste w okresie treningowym. Linia czerwona – dane rzeczywiste w okresie testowym. Gruba niebieska – to predykcja. Te mniej i bardziej szare pola to zakres dla 80% i 95% pewności przewidywania.
Jak widać predykcja jest dość trafna (niebieska linia blisko czerwonej). Możemy uznać, że model jest całkiem niezły.
Możemy sprawdzić jeszcze “rozjazd oczekiwań z rzeczywistością” – dobrą miarą jest błąd średniokwadratowy RMSE (czyli pierwiastek ze średniej kwadratów odchyleń) 0.2397 – ale uwaga, jest to błąd mierzony na próbce treningowej! Błędy na próbkach testowych zobaczymy za chwilę.
Model ETS
Dokładnie to samo co w przypadku ARIMA zrobimy teraz z użyciem modelu innej klasy: ETS – wygładzanie wykładnicze.
|
1 2 3 4 5 |
bezrobocie_ts_ets <- ets(bezrobocie_ts_learn) bezrobocie_ts_ets_forecast <- forecast(bezrobocie_ts_ets, h = length(bezrobocie_ts_test)) plot(bezrobocie_ts_ets_forecast) lines(bezrobocie_ts_test, col = "red") |
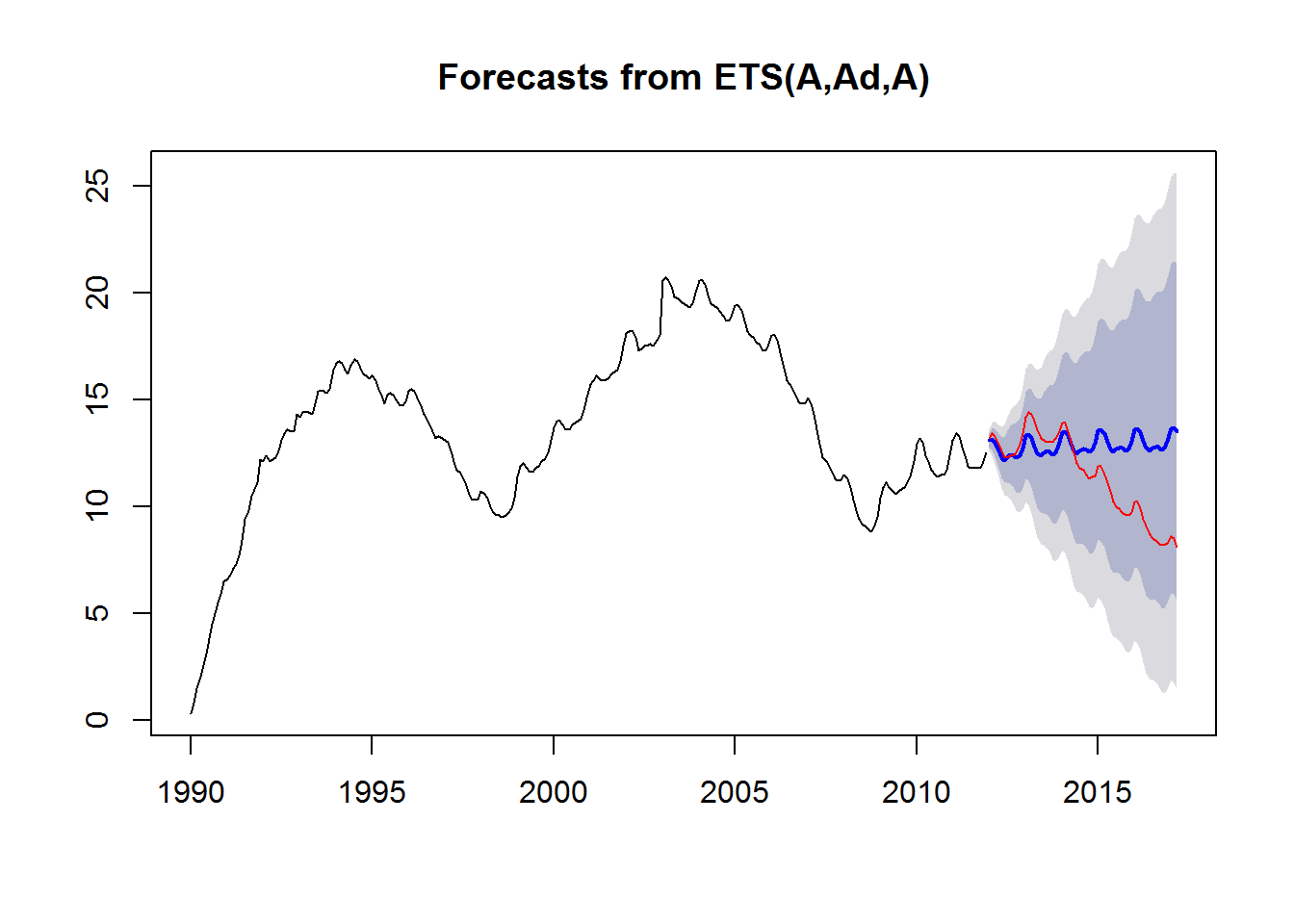
Tutaj mamy rozjazd nieco większy (błąd RMSE to 0.2574), ale wciąż trzyma się to w zakresie 80% pewności. Mniej więcej w podobnym momencie w obu predykcjach wartości prognozowane zaczynają odjeżdżać od rzeczywistych.
Porównanie modeli
Oprócz RMSE jest jeszcze kilka innych współczynników, które możemy porównać:
|
1 2 |
# ARIMA: accuracy(bezrobocie_ts_arima_forecast, bezrobocie_ts_test) |
|
1 2 3 4 5 6 |
## ME RMSE MAE MPE MAPE ## Training set -0.003142293 0.2396762 0.1516077 0.03308766 1.204893 ## Test set -0.425392882 1.4920106 1.2292393 -6.11695196 12.131009 ## MASE ACF1 Theil's U ## Training set 0.07486798 -0.006814556 NA ## Test set 0.60703175 0.964862387 6.14694 |
|
1 2 |
# ETS: accuracy(bezrobocie_ts_ets_forecast, bezrobocie_ts_test) |
|
1 2 3 4 5 6 |
## ME RMSE MAE MPE MAPE ## Training set 0.00326782 0.2573613 0.1724841 0.08392356 2.08705 ## Test set -1.39763601 2.4379754 1.8158624 -15.76441507 18.85619 ## MASE ACF1 Theil's U ## Training set 0.08517734 0.2585715 NA ## Test set 0.89672219 0.9598943 10.41732 |
Tutaj widać m.in. RMSE dla próbek testowych – w przypadku ETS jest to 2.4, dla ARIMA – 1.5. Inne współczynniki też przemawiają na korzyść ARIMA (im niższe tym lepiej).
Teraz – mając już opracowane modele spróbujmy rzeczywiście przewidzieć przyszłość, a nie tylko sprawdzić przewidywania z tym co już wiemy.
Jaka będzie stopa bezrobocia za dwa lata?
Zamiast danych treningowych użyjemy pełnej historii i prognozujemy kolejne dwa lata (24 miesięczne okresy):
|
1 2 3 4 5 |
bezrobocie_ts_arima <- auto.arima(bezrobocie_ts) bezrobocie_ts_arima_forecast <- forecast(bezrobocie_ts_arima, h = 24) plot(bezrobocie_ts_arima_forecast) abline(h=8.1, col="red") |
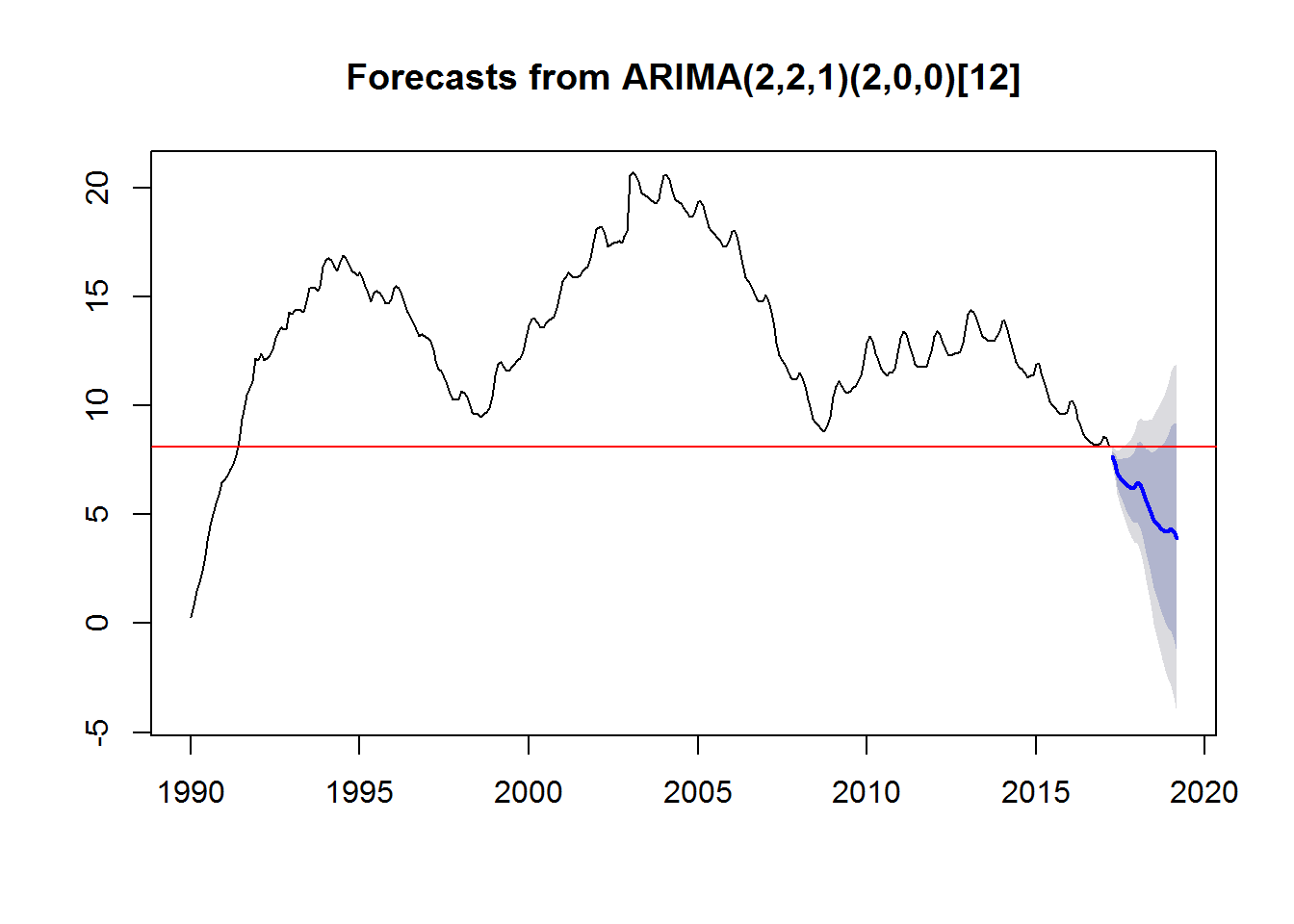
Czerwoną linią zaznaczyłem ostatnią znaną wartość stopy bezrobocia (8.1% za marzec 2017).
Być może nie widać tego dokładnie – powiększy tylko kawałek prognozowany:
|
1 |
plot(bezrobocie_ts_arima_forecast$mean) |
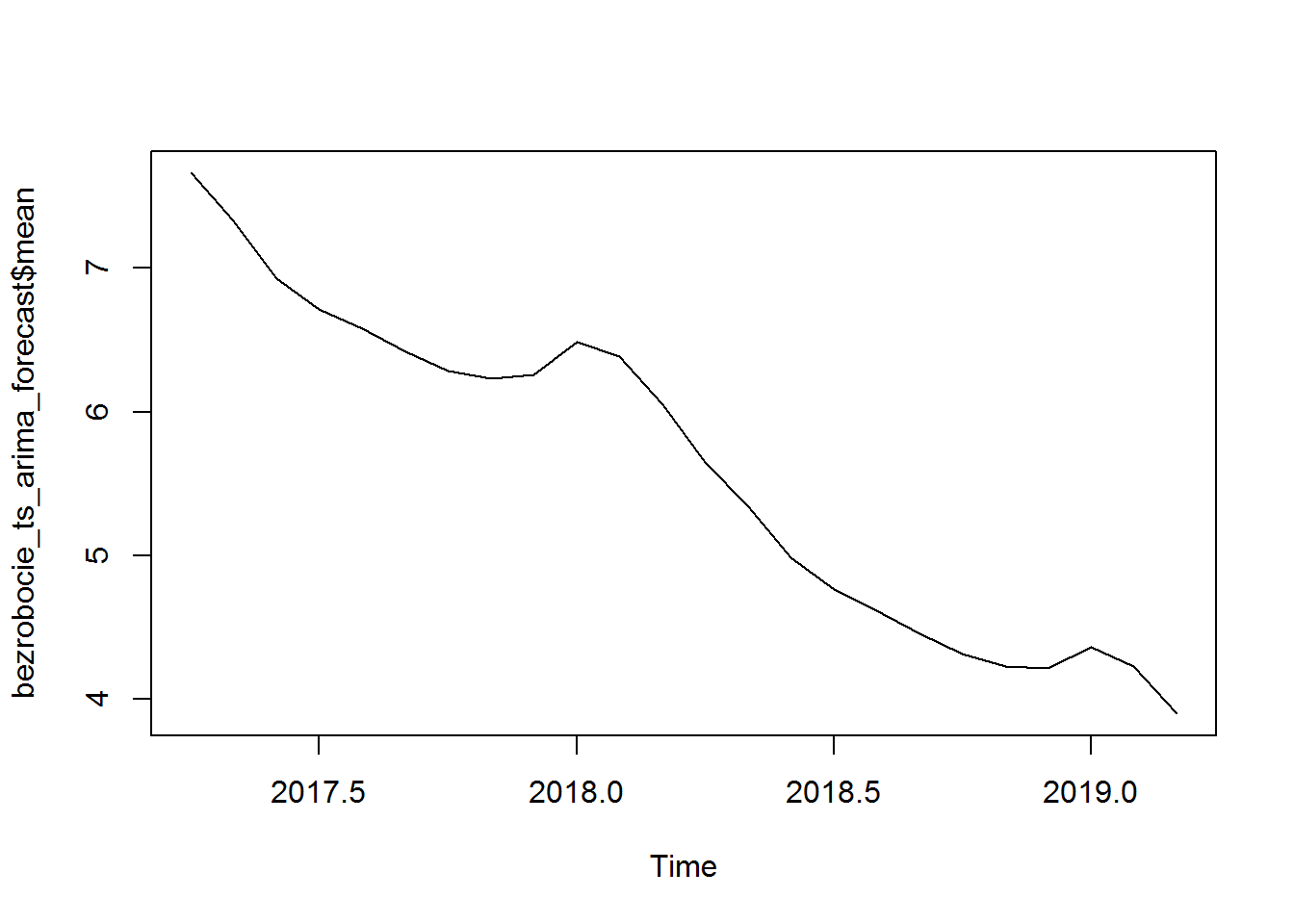
Widzimy zachowanie “górki” w początku roku 2018 i 2019. Dobrze to wróży.
Wygląda z naszej prognozy, że w lutym 2019 stopa bezrobocia będzie na poziomie 3.9%, co wydaje mi się nierealne. Za rok, w lutym 2018, byłoby to według naszego prostego modelu 6.1%, co jest zdecydowanie bardziej prawdopodobne.
Wydłużając prognozę na 240 okresy (czyli 20 lat) zerowe bezrobocie osiągniemy w maju 2021 roku. Co jest oczywistą bzdurą. Dlatego do prognozowania tego typu danych należy przede wszystkim użyć innych modeli (biorących pod uwagę wiele czynników, a nie tylko historię) i nie prognozować na tak długi okres. Rok to już według mnie wróżenie z fusów.
Jeśli chcemy oprzeć się na historii – branie do modelu zakresu dłuższego niż 10 lat w przypadku tak zmiennych danych nie ma sensu.
Spróbujmy więc przewidzieć stopę bezrobocia w najbliższym roku na podstawie danych z ostatnich 5 lat.
Korzystając (z jak dotychczas “lepszego”) modelu ARIMA:
|
1 2 3 4 |
bezrobocie_ts_arima <- auto.arima(window(bezrobocie_ts, start = c(2012, 1))) bezrobocie_ts_arima_forecast <- forecast(bezrobocie_ts_arima, h = 12) plot(bezrobocie_ts_arima_forecast) abline(h=8.1, col="red") |
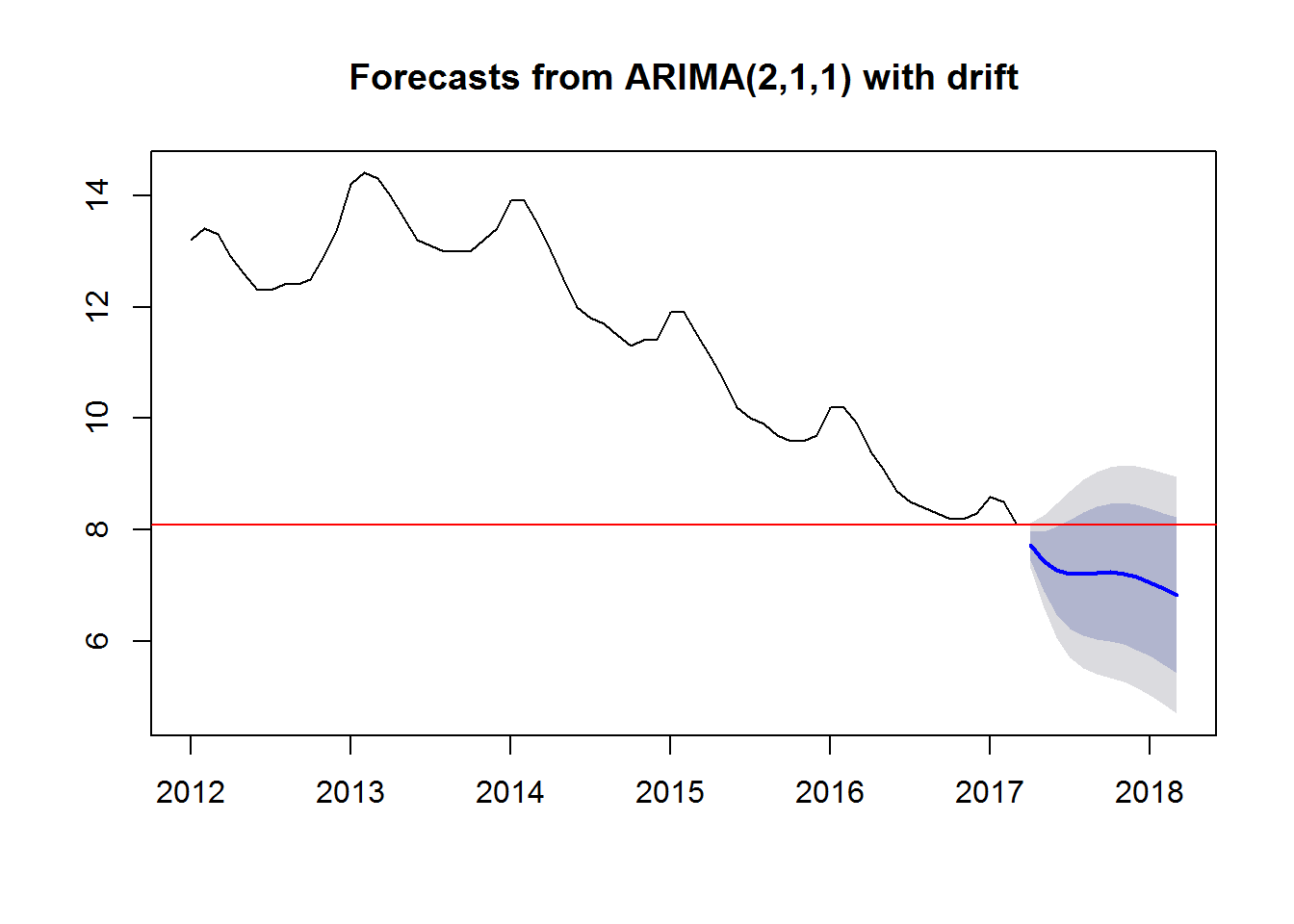
W modelu klasy ETS:
|
1 2 3 4 5 6 |
bezrobocie_ts_ets <- ets(window(bezrobocie_ts, start = c(2012, 1))) bezrobocie_ts_ets_forecast <- forecast(bezrobocie_ts_ets, h = 12) plot(bezrobocie_ts_ets_forecast) abline(h=8.1, col="red") lines(bezrobocie_ts_arima_forecast$mean, col="green") |
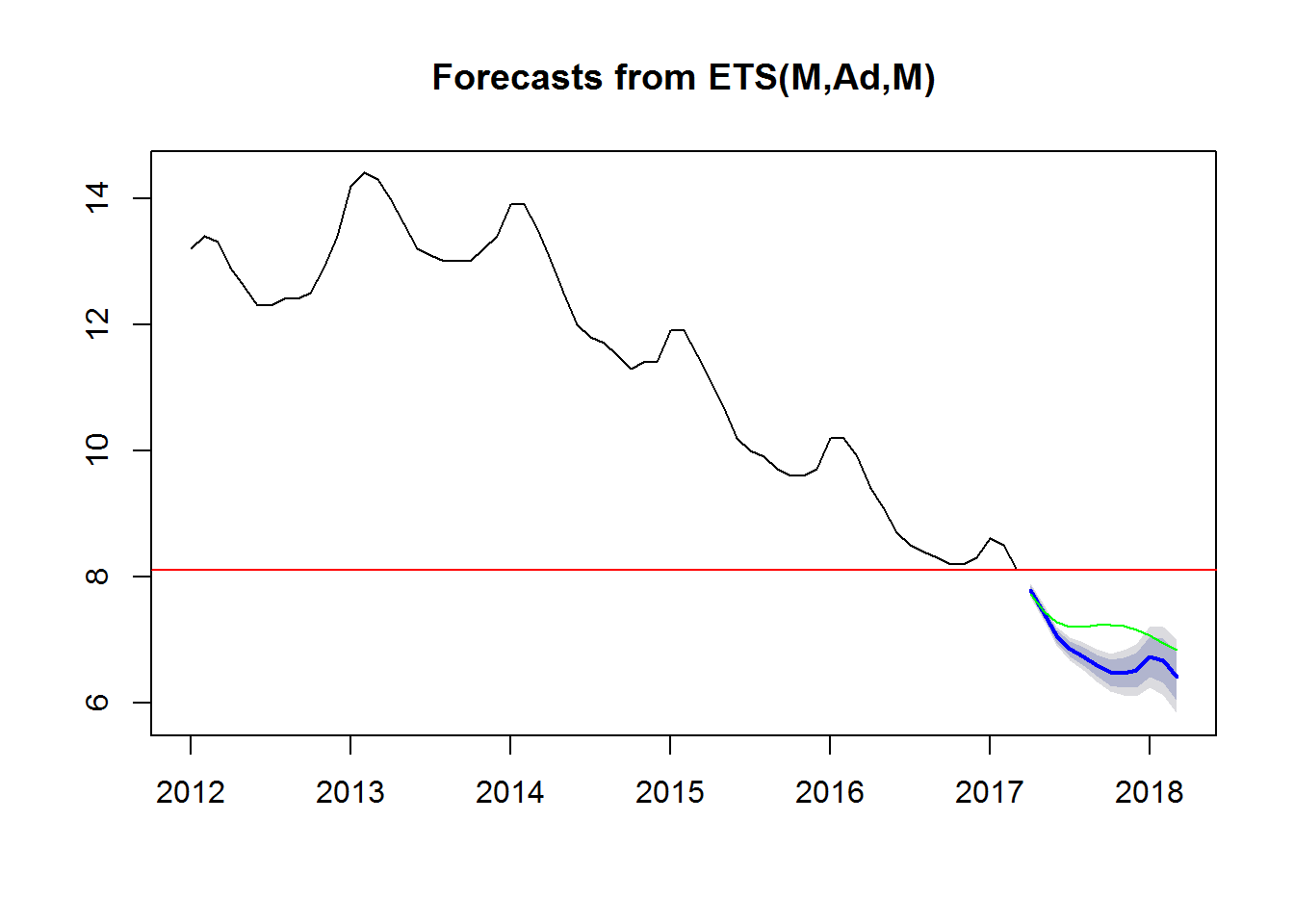
ETS jak widać daje węższy zakres niepewności. Zielona linia to predykcja z modelu ARIMA. W modelu ETS zachowana została “wiosenna” górka, której brak w prognozie według ARIMA.
Czy którykolwiek z modeli się sprawdzi? Na to trzeba niestety poczekać.
Pingback: Nowe pojazdy w Polsce po 2010 roku | Łukasz Prokulski
Mamy wyniki za kwiecień – 7,7%
Zgodnie z przewidywaniami opisanymi w poście – stopa bezrobocia za kwiecień miała wynosić:
Aby to sprawdzić trzeba wypisać wyniki, czyli po prostu w konsoli wpisać na sam koniec: bezrobocie_ts_arima_forecast i bezrobocie_ts_ets_forecast
Super analiza! :) Łukasz, dwie rzeczy:
1. Bardzo przyjemnie się czyta. Idealne do popołudniowej kawy podczas urlopu.
2. Dużo można się z Twoich analiz nauczyć. Jestem pełen podziwu za profesjonalne podejście i drobiazgowość.
Chapeau bas! :)
Dziękuję za miłe słowa i… przyjemnego urlopu :)
Pingback: Bezrobocie spada, bo wszyscy wyjechali? | Łukasz Prokulski
Lukasz, swietne artykuly na bardzo wysokim poziomie technicznym i merytorycznym. Mysle, ze aby tak dalej a niebawem ktos rozsadny zauwazy Twoja profesjonalna wiedze w tym temacie i bedziesz niczym SPIN DOCTOR INTELIGENCE pomagal wielkim partjom czy korporacjom analizowac i co wazne przewidywac przyszlosc. Wielki szacunek za dzielenie sie takimi ciekawymi tematami. Wsrod tego calego szumu informacyjnego dzis w sieci niewielu jest takich jak Ty. A znane jest przeciez powiedzenie: „W starożytności władzę miał ten kto miał dostęp do informacji, dziś władzę ma ten kto wie jakie informacje ignorować –
YUVAL NOAH HARARI” Czekam na jakis Twoj poradnik dla poczatkujacych „Krok po kroku” jak od strony programistycznej rozpoczac nauke tworzenia takich analiz, w szczegolnosci agregowania tresci roznego typu. Pozdrawiam