Jak będzie oceniony film, który dopiero powstaje? Czyli o wybieraniu i poprawianiu modeli predykcyjnych.
W poprzednim wpisie pokazałem dane zgromadzone z Filmwebu w różnych przekrojach, a na koniec zaproponowałem model, który na podstawie informacji o ocenach filmów twórców (reżyseria, scenariusz, autorzy muzyki oraz zdjęć) i aktorów próbuje przewidzieć ocenę nowego filmu (wyprodukowanego w tym samym składzie). Nurtował mnie ten pomysł, postanowiłem go więc nieco lepiej przeanalizować. A przy okazji – nauczyć się budować modele predykcyjne (chociaż o nich trochę już wiem – był wpis o klasyfikacji).
Jeśli nie znasz poprzedniego wpisu – zachęcam do lektury! klik, klik
Na początek przygotujemy środowisko, wczytamy zgromadzone dane i ustalimy jaka jest minimalna liczba głosów na film, żeby w ogóle się nim zajmować.
|
1 2 3 4 5 6 7 8 9 10 11 |
library(tidyverse) theme_set(theme_minimal()) # ustawienie generatora losowego # dla powtarzalności wyników set.seed(123456) load("filmweb_data.rda") minFilmVotes <- quantile(movies$FilmVotes, 0.7, na.rm = TRUE) |
Model zakłada, że na ocenę filmu mają dotychczasowe dokonania jego twórców. Zrobimy zatem tak:
- dla losowego filmu sprawdzimy kto jest jego twórcą (mamy 5 ról: reżysera, autorów scenariusza, zdjęć i muzyki oraz aktorów)
- dla każdej z tych osób policzymy średnią ze wszystkich filmów, w których produkcji dana osoba brała udział w tej samej roli. To ma znaczenie i działa tak, że jeśli rozpatrujemy Woody’ego Allena jako reżysera liczymy średnią z filmów przez niego wyreżyserowanych, a jeśli patrzymy na niego jako aktora – liczymy średnią z filmów w których występował. Dla Allena możemy mieć
trzycztery różne średnie (i każda może być inna!): jako reżyser (7.081), scenarzysta (7.057), aktor (7.059) i twórca muzyki (7.129 – Allen najlepszy jako kompozytor, LOL) - mając wszystkie średnie dla osób w danej roli – liczymy zbiorczą średnią (średnią ze średnich). Tym sposobem mamy średnią reżyserii, średnią scenariusza, średnią zdjęć, muzyki i aktorów. Te pięć wartości to będą nasze zmienne niezależne (czyli parametry wejściowe)
Zmienną zależną (czyli przewidywaną przez model) będzie ocena filmu. Pod uwagę weźmiemy modele, które trzeba “wytrenować” – potrzebujemy dlatego znać prawdziwą ocenę filmu.
Na potrzeby przygotowania danych, na których będziemy budować modele przygotujemy dwie funkcje:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
PersonMean <- function(person_ID, role_ID) { # znajdź wszystkie filmy z podaną osobą w podanej roli # ale tylko ze znaczącą liczbą ocen person_movies <- persons_in_movies %>% filter(roleID == role_ID, personID == person_ID) %>% select(filmID) %>% distinct() %>% inner_join(movies, by="filmID") %>% filter(FilmVotes >= minFilmVotes) # policz średnią z ocen tych filmów mean_score <- mean(person_movies$filmRate, na.rm = TRUE) return(mean_score) } MovieMakersMean <- function(film_ID, role_ID) { # znajdź osoby z filmu w danej roli person_ID <- persons_in_movies %>% filter(filmID==film_ID, roleID == role_ID) %>% select(personID) %>% distinct() # dla wyszystkich IDków osób policz średnią ich dokonań w odpowierniej roli # a później średnią z tej średniej mean_score <- mean(apply(person_ID, 1, function(x) PersonMean(x, role_ID)), na.rm = TRUE) return(mean_score) } |
Co robią funkcje napisane jest w komentarzach zawartych w ich kodzie. Dla laików nie ma to znaczenia ;)
Próbka danych
Żeby było co trenować potrzebujemy danych. Im więcej tym lepiej. Ale rozsądnie. Na początek spróbujmy z pięcioma tysiącami losowo wybranych filmów. Losujemy sobie więc numery filmów, a później dla każdego z numerów szukamy średnich z dokonań twórców. To długi proces – można iść na obiad, do kina, wyjechać na weekend… U mnie zajęło to jakieś 12 godzin.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 |
# rozmiar próbki z filmami n_sample_size <- 5000 # numery filmów - n_sample_size sztuk, z odpowiednią liczbą ocen film_IDs <- movies %>% filter(FilmVotes >= minFilmVotes) %>% select(filmID) %>% distinct() %>% sample_n(n_sample_size, replace = FALSE) %>% .$filmID # tabelka na dane treningowe sample_df <- data.frame() for(i in 1:length(film_IDs)) { print(i) sample_df <- rbind(sample_df, data.frame( # ocena filmu: filmRate = as.numeric(movies[movies$filmID == film_IDs[i], "filmRate"]), # reżyser: dirRate = MovieMakersMean(film_IDs[i], 1), # scenarzysta: scrRate = MovieMakersMean(film_IDs[i], 2), # muzyka: musRate = MovieMakersMean(film_IDs[i], 3), # zdjęcia: photoRate = MovieMakersMean(film_IDs[i], 4), # aktorzy: actRate = MovieMakersMean(film_IDs[i], 6), # tytuł filmu: filmTitle = as.character(movies[movies$filmID == film_IDs[i], "filmTitle"]), # ID w bazie Filmweb: filmID = film_IDs[i], stringsAsFactors = FALSE)) } # NA na średnie z kolumn sample_df$dirRate <- ifelse(is.na(sample_df$dirRate), mean(sample_df$dirRate, na.rm = TRUE), sample_df$dirRate) sample_df$scrRate <- ifelse(is.na(sample_df$scrRate), mean(sample_df$scrRate, na.rm = TRUE), sample_df$scrRate) sample_df$musRate <- ifelse(is.na(sample_df$musRate), mean(sample_df$musRate, na.rm = TRUE), sample_df$musRate) sample_df$photoRate <- ifelse(is.na(sample_df$photoRate), mean(sample_df$photoRate, na.rm = TRUE), sample_df$photoRate) sample_df$actRate <- ifelse(is.na(sample_df$actRate), mean(sample_df$actRate, na.rm = TRUE), sample_df$actRate) |
Mając wylosowane filmy podzielimy je sobie na część treningową danych oraz na część testową, na której będziemy weryfikować nasze kolejne modele:
|
1 2 3 4 5 6 7 8 |
# losowe 80% wierszy train_n <- sample(1:nrow(sample_df), 0.8 * nrow(sample_df)) # próbka treningowa - 80% means_train_df <- sample_df[train_n, ] # próbka testowa - 20% (to, co nie weszsło do treningowej) means_test_df <- sample_df[setdiff(1:5000, train_n), ] |
Modele
Przygotujemy trzy modele regresyjne, rożnych kategorii. Wybierzemy najlepszy i będziemy ten najlepszy modyfikować.
Na początek najprostszy model – regresja liniowa
|
1 2 3 4 5 6 7 8 9 |
model_lm <- lm(filmRate ~ dirRate + scrRate + musRate + photoRate + actRate, means_train_df) # predykcja means_test_df$predRate_lm <- predict(model_lm, newdata = means_test_df[,2:6]) # podsumowanie modelu: summary(model_lm) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
## ## Call: ## lm(formula = filmRate ~ dirRate + scrRate + musRate + photoRate + ## actRate, data = means_train_df) ## ## Residuals: ## Min 1Q Median 3Q Max ## -2.77501 -0.18511 -0.00206 0.19375 2.06037 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) -2.38389 0.05616 -42.445 < 2e-16 *** ## dirRate 0.16553 0.01421 11.645 < 2e-16 *** ## scrRate 0.29918 0.01425 20.992 < 2e-16 *** ## musRate 0.05148 0.01172 4.393 1.15e-05 *** ## photoRate -0.05750 0.01213 -4.742 2.20e-06 *** ## actRate 0.90701 0.01900 47.749 < 2e-16 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.3504 on 3994 degrees of freedom ## Multiple R-squared: 0.8891, Adjusted R-squared: 0.889 ## F-statistic: 6406 on 5 and 3994 DF, p-value: < 2.2e-16 |
Powyższe informacje to podsumowanie tego co policzyła nam maszyna. Są to kolejne współczynniki (ich wartości to kolumna Estimate) z równania:
![]()
W kolumnie Pr(>|t|) jest wartość p-value, która określa istotność danej zmiennej w modelu. Wszystkie tutaj są na poziomie wręcz idealnym (zwykle przyjmuje się p-value = 0.05 jako bardzo dobrą wartość), nie byłoby czego zmieniać – od pierwszego strzału mamy super model! Czy aby na pewno? Przekonamy się za chwilę.
Zobaczmy jak przewidziane oceny filmów mają się do wartości rzeczywistych:
|
1 2 3 4 5 6 7 |
ggplot(means_test_df) + geom_point(aes(filmRate, predRate_lm), color="lightgreen", alpha=0.8) + geom_abline(slope = 1, color="blue") + xlim(0,10) + ylim(0,10) + labs(x = "Ocena oryginalna", y = "Predykcja", title = "Model: regresja liniowa") |
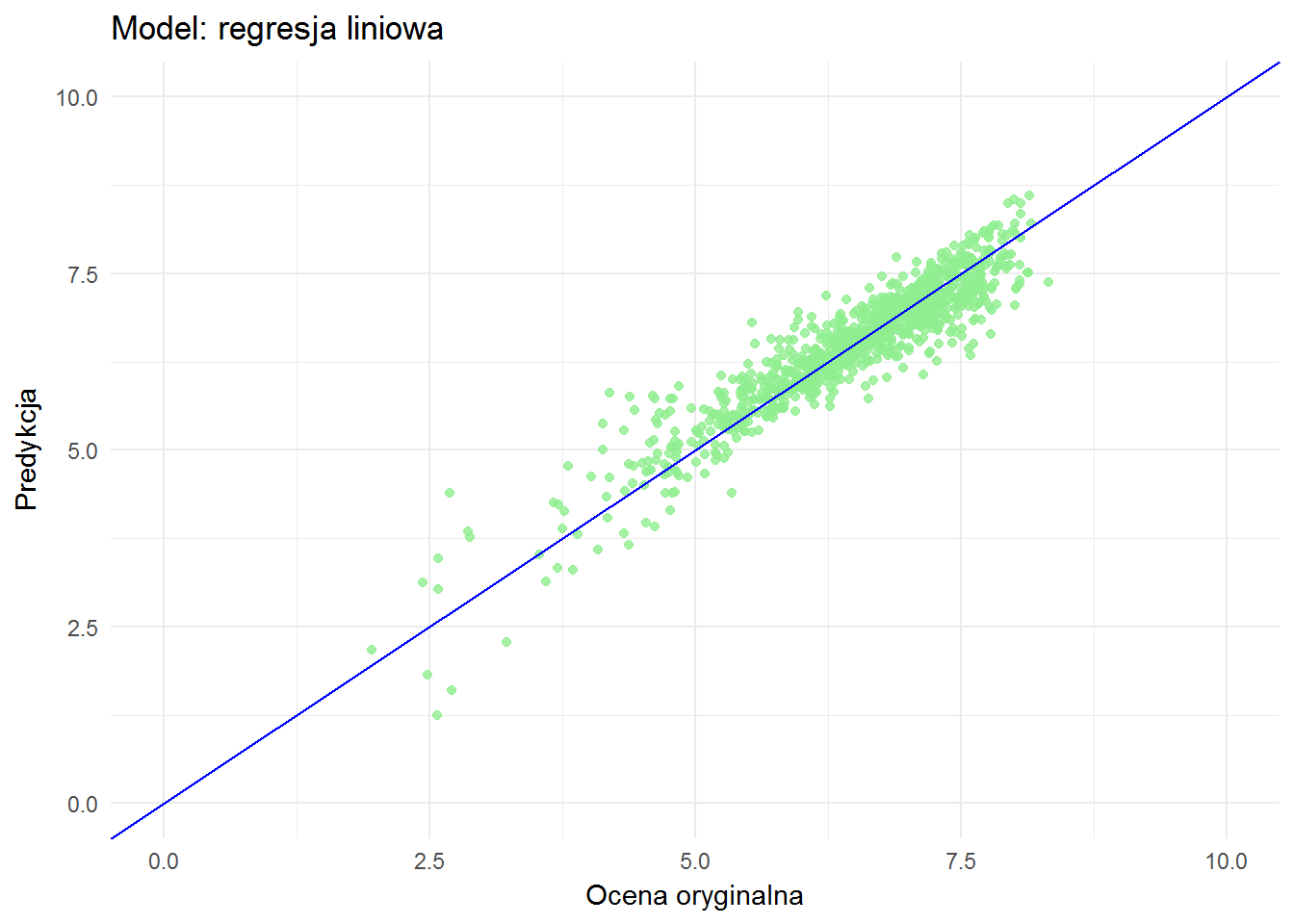
Idealnie byłoby, gdyby wszystkie punkty ułożyły się na niebieskiej prostej. A jak widać tak nie jest. Ale jest całkiem dobrze.
Z opisu metod klasyfikacji pamiętamy, że dobrym modelem jest random forest. Przekonajmy się czy tak jest też dla zagadnień regresji:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
library(randomForest) model_rf <- randomForest(filmRate ~ dirRate + scrRate + musRate + photoRate + actRate, means_train_df, type = "regression", ntree = 500, importance = TRUE) means_test_df$predRate_rf <- predict(model_rf, newdata = means_test_df[,2:6]) ggplot(means_test_df) + geom_point(aes(filmRate, predRate_rf), color="lightgreen", alpha=0.8) + geom_abline(slope = 1, color="blue") + xlim(0,10) + ylim(0,10) + labs(x = "Ocena oryginalna", y = "Predykcja", title = "Model: random forest") |
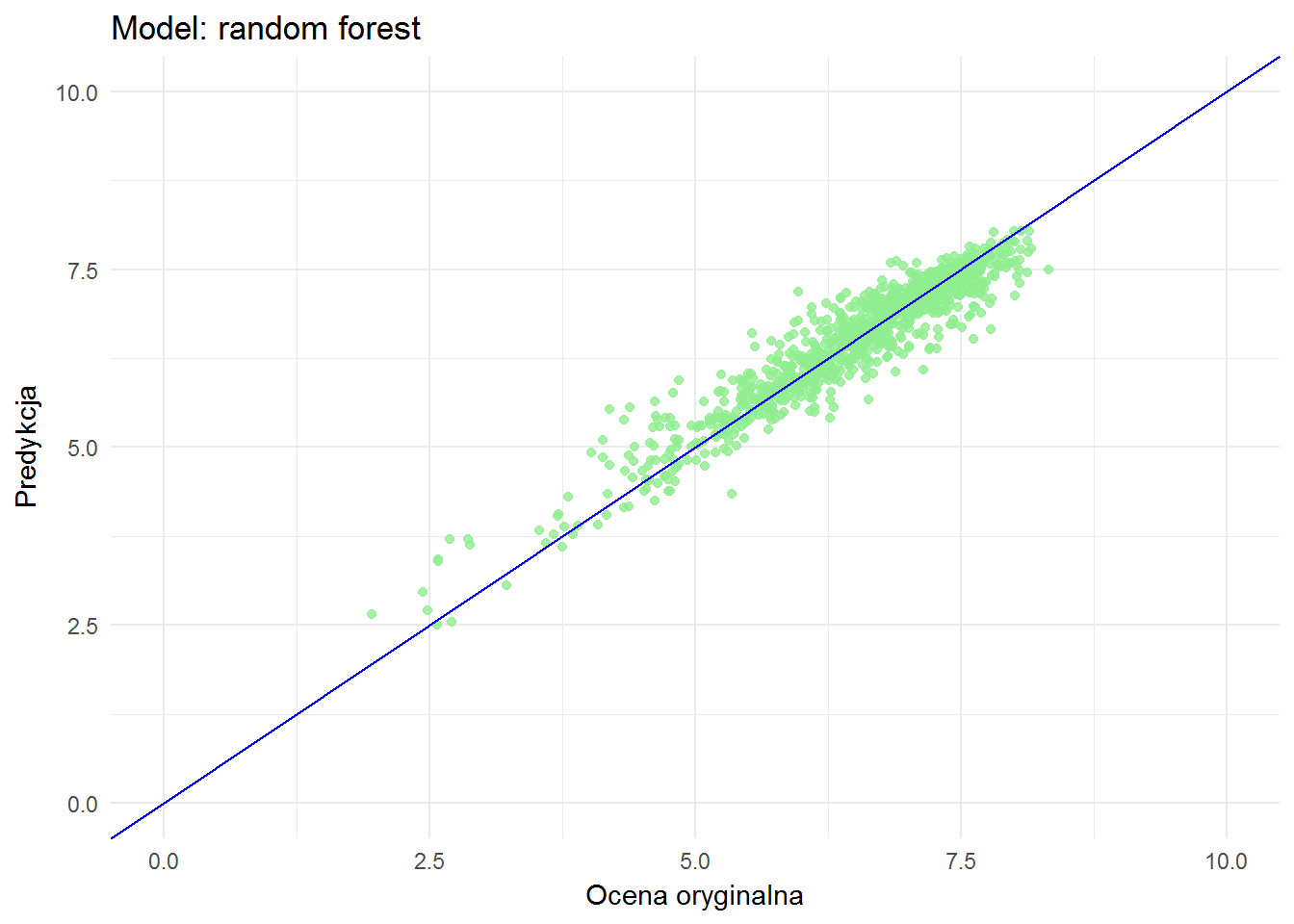
Wygląda podobnie, chociaż widać różnice dla niskich ocen: punkty są bardziej odległe od niebieskiej prostej dla regresji liniowej.
To na koniec sprawdźmy model klasy SVM:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
library(e1071) model_svm <- svm(filmRate ~ dirRate + scrRate + musRate + photoRate + actRate, means_train_df, type = "eps-regression") means_test_df$predRate_svm <- predict(model_svm, newdata = means_test_df[,2:6]) ggplot(means_test_df) + geom_point(aes(filmRate, predRate_svm), color="lightgreen", alpha=0.8) + geom_abline(slope = 1, color="blue") + xlim(0,10) + ylim(0,10) + labs(x = "Ocena oryginalna", y = "Predykcja", title = "Model: SVM") |
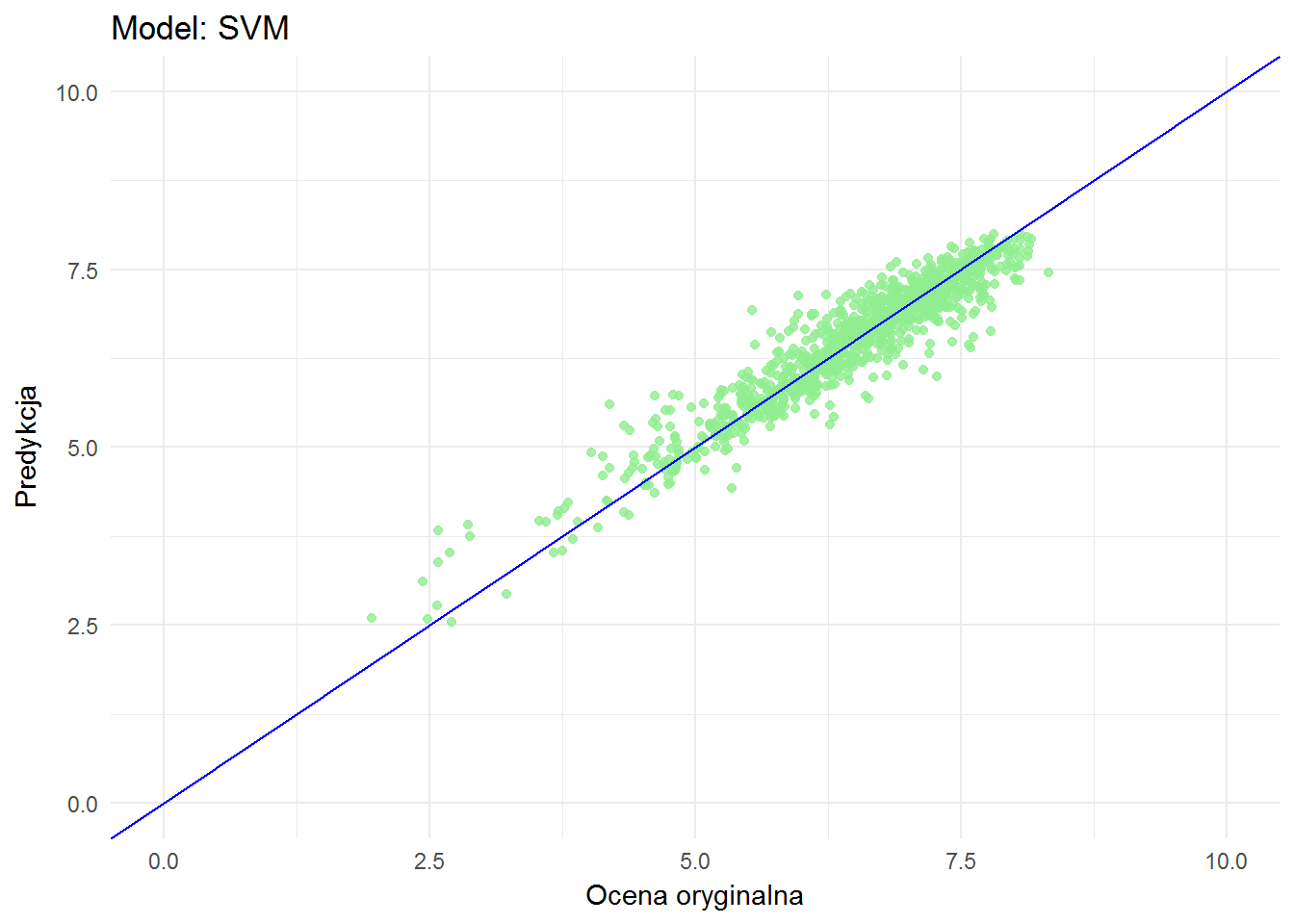
Na pierwszy rzut oka niewiele różni się od random forest. Jak więc porównać modele ze sobą?
Porównanie modeli
Na początek zobaczmy jak wygląda rozkład przewidzianych ocen w zależności od modelu w zestawieniu z prawdziwymi ocenami (gruba czarna linia):
|
1 2 3 4 5 6 7 |
ggplot(means_test_df) + geom_density(aes(filmRate), color="black", size=2, alpha=0.2) + geom_density(aes(predRate_svm), fill="green", alpha=0.2) + geom_density(aes(predRate_rf), fill="blue", alpha=0.2) + geom_density(aes(predRate_lm), fill="red", alpha=0.2) + xlim(0,10) + labs(x="Predykcja", y="Gęstość prawdopodobieństwa") |
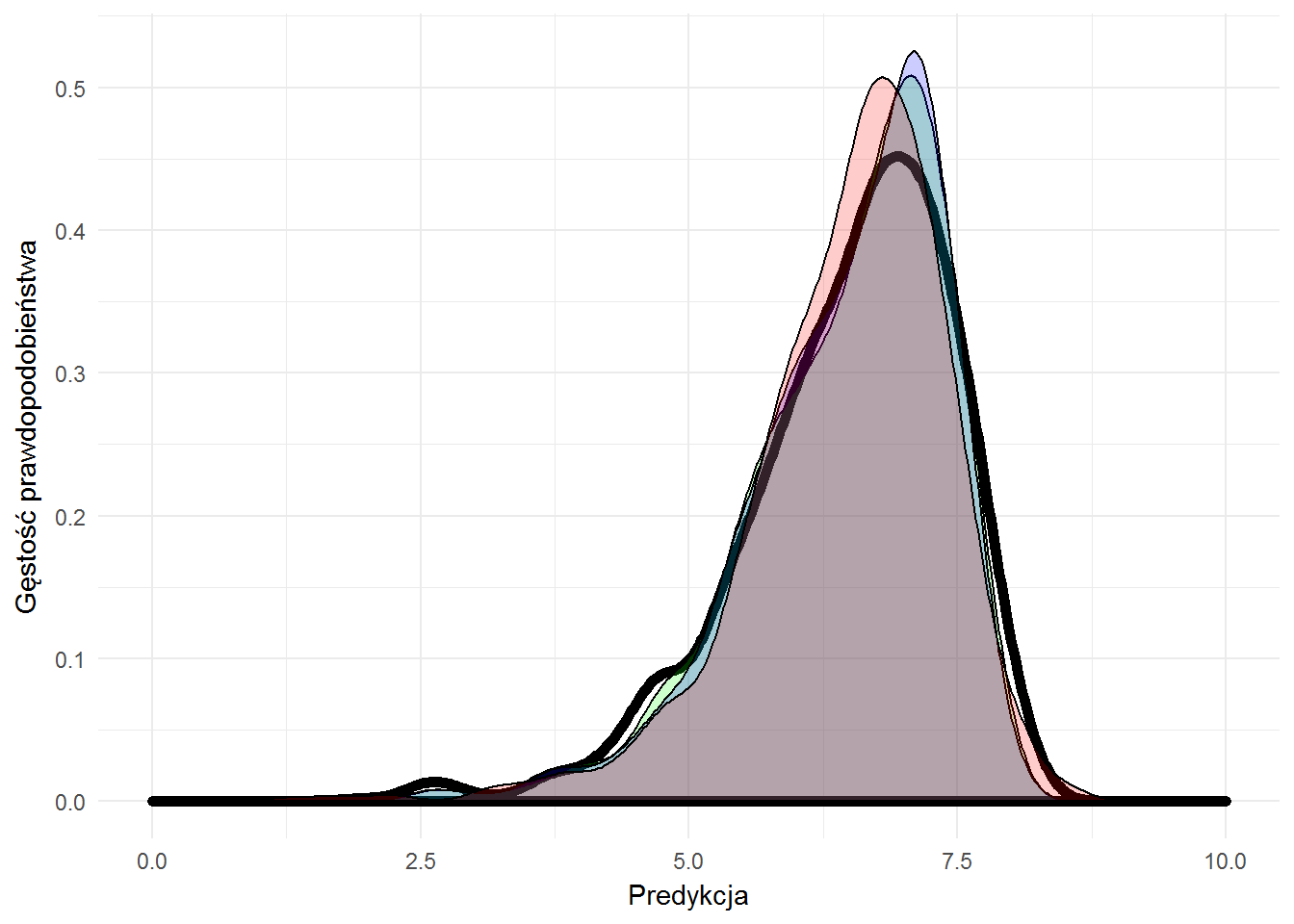
Już lepiej widać różnice – zarówno pomiędzy modelami jak i prawdziwymi wartościami. Cóż – idealnie nie jest… Ale też nie musi być idealnie. Ważne, żeby było wystarczająco dobrze :) A tutaj jest bardzo dobrze!
Różnice da się ocenić kilkoma współczynnikami liczbowymi. Zajmiemy się trzema najprostszymi: R2, jego nieco zmodyfikowaną wersją adj R2 oraz błędem średniokwadratowym.
Zaczniemy od R-squared, który po polsku nazywa się współczynnikiem determinacji i w postaci liczby pomiędzy zerem a jedynką określa jak bardzo dobrze dopasowany jest model. Im bliżej jedynki tym lepiej.
W polskiej Wikipedii są nieco inne definicje współczynnika niż w wersji angielskiej, idea jest ta sama (i zapewne po przekształceniach wychodzi na to samo) – skorzystamy z wersji angielskiej (taką widziałem też w jednym z kursów na Udemy):
![]()
Jak widać potrzebujemy dwóch wartości – ![]() oraz
oraz ![]() :
:
![]() to miara odchylenia wartości rzeczywistych
to miara odchylenia wartości rzeczywistych ![]() od średniej
od średniej ![]() tych wartości:
tych wartości:
![]()
zaś ![]() to miara różnicy pomiędzy wartościami wyliczonymi
to miara różnicy pomiędzy wartościami wyliczonymi ![]() a wartościami prawdziwymi
a wartościami prawdziwymi ![]() :
:
![]()
|
1 2 3 4 5 6 7 8 9 |
SS_tot <- sum((means_test_df$filmRate - mean(means_test_df$filmRate))^2) SS_res_lm <- sum((means_test_df$filmRate - means_test_df$predRate_lm)^2) SS_res_rf <- sum((means_test_df$filmRate - means_test_df$predRate_rf)^2) SS_res_svm <- sum((means_test_df$filmRate - means_test_df$predRate_svm)^2) R2_lm <- 1 - SS_res_lm/SS_tot R2_rf <- 1 - SS_res_rf/SS_tot R2_svm <- 1 - SS_res_svm/SS_tot |
Zobaczmy otrzymane wartości R-kwadrat dla poszczególnych modeli:
| Model | Wartość R2 |
|---|---|
| regresja liniowa | 0.868098 |
| random forest | 0.8954855 |
| SVM | 0.8915317 |
Jak widać najbliżej jedynki jest random forest.
Miara Adjusted R-squared – to zmodyfikowany R2 (im bliżej jedynki tym lepiej – tak samo) w następujący sposób:
![]()
gdzie:
- n – liczność próby
- k – liczba zmiennych niezależnych (k=5 w naszym przypadku)
Miara ta wprowadzona jest z powodu rosnącego R2 w przypadku dodawania nowych zmiennych niezależnych do modelu. Niekoniecznie dodanie nowych zmiennych poprawia model, ale zawsze przybliża R2 do jedynki. adjR2 jest swego rodzaju lekarstwem – uwzględnia liczbę zmiennych w modelu (k). Im więcej zmiennych tym większe k i tym samym większy mianownik, a to daje mniejsze wartości całego ułamka i jednocześnie oddala od jedynki. Ale z drugiej strony R2 rośnie… trwa zatem nieustanna walka. Policzmy adjR2 dla naszych modeli:
|
1 2 3 |
AdjR2_lm <- 1 - (1-R2_lm)*(nrow(means_test_df)-1)/(nrow(means_test_df)-5-1) AdjR2_rf <- 1 - (1-R2_rf)*(nrow(means_test_df)-1)/(nrow(means_test_df)-5-1) AdjR2_svm <- 1 - (1-R2_svm)*(nrow(means_test_df)-1)/(nrow(means_test_df)-5-1) |
| Model | Wartość adj R2 |
|---|---|
| regresja liniowa | 0.8674345 |
| random forest | 0.8949598 |
| SVM | 0.8909861 |
Znowu wygrywa random forest.
Na koniec został błąd średniokwadratowy (mean squared error), czyli średnia miara różnicy pomiędzy wartościami prawdziwymi a przewidywanymi (to już mamy w SSres). Tutaj im mniej tym lepiej.
![]()
Sprawdźmy modele:
|
1 2 3 |
MSE_lm <- SS_res_lm/nrow(means_test_df) MSE_rf <- SS_res_rf/nrow(means_test_df) MSE_svm <- SS_res_svm/nrow(means_test_df) |
| Model | Wartość MSE |
|---|---|
| regresja liniowa | 0.1307313 |
| random forest | 0.1035868 |
| SVM | 0.1075055 |
Niespodzianki nie ma.
Zajmijmy się zatem optymalizacją modelu opartego o metodę random forest.
Optymalizacja modelu
Wprost z modelu możemy uzyskać informacje o “ważności” poszczególnych zmiennych zależnych:
|
1 |
importance(model_rf, type=1) |
|
1 2 3 4 5 6 |
## %IncMSE ## dirRate 27.82332 ## scrRate 28.98359 ## musRate 26.16962 ## photoRate 22.99829 ## actRate 41.86839 |
Według powyższych danych najmniej “ważną” w modelu zmienną niezależną jest photoRate. Spróbujmy zbudować model bez tej zmiennej i zobaczymy jakie mamy wartości R2, adj R2 i MSE.
Dlaczego tak? Bo jedna z metod ulepszania modelu to dodawanie lub odejmowanie zmiennych niezależnych. My zaczęliśmy od wszystkich, więc będziemy usuwać kolejne zmienne. Za każdym razem tą najmniej znaczącą (najmniejsza wartość p-value w regresji liniowej, a w naszym przypadku %IncMSE). I robimy to tak długo, dopóki miary modelu będą się poprawiać. Jak przestaną to znaczy że mamy najlepszy model (ten, który miał najlepsze miary oczywiście).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
model_rf <- randomForest(filmRate ~ dirRate + scrRate + musRate + actRate, means_train_df, type = "regression", ntree = 500, importance = TRUE) means_test_df$predRate_rf <- predict(model_rf, newdata = means_test_df[,2:6]) SS_res_rf <- sum((means_test_df$filmRate - means_test_df$predRate_rf)^2) R2_rf_1 <- 1 - SS_res_rf/SS_tot AdjR2_rf_1 <- 1 - (1-R2_rf)*(nrow(means_test_df)-1)/(nrow(means_test_df)-4-1) MSE_rf_1 <- SS_res_rf/nrow(means_test_df) |
| Współczynnik | Wartość |
|---|---|
| R2 | 0.8948707 |
| adj R2 | 0.8950654 |
| MSE | 0.1041962 |
Sprawdźmy czy jeszcze jakąś zmienną można usunąć z modelu?
|
1 |
importance(model_rf, type=1) |
|
1 2 3 4 5 |
## %IncMSE ## dirRate 26.48396 ## scrRate 29.06703 ## musRate 26.66934 ## actRate 46.91318 |
Czas na dirRate – ponownie budujemy model i sprawdzamy otrzymane wyniki:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
model_rf <- randomForest(filmRate ~ scrRate + musRate + actRate, means_train_df, type = "regression", ntree = 500, importance = TRUE) means_test_df$predRate_rf <- predict(model_rf, newdata = means_test_df[,2:6]) SS_res_rf <- sum((means_test_df$filmRate - means_test_df$predRate_rf)^2) R2_rf_2 <- 1 - SS_res_rf/SS_tot AdjR2_rf_2 <- 1 - (1-R2_rf)*(nrow(means_test_df)-1)/(nrow(means_test_df)-3-1) MSE_rf_2 <- SS_res_rf/nrow(means_test_df) |
| Współczynnik | Wartość |
|---|---|
| R2 | 0.891335 |
| adj R2 | 0.8951707 |
| MSE | 0.1077005 |
Może jeszcze coś można usunąć?
|
1 |
importance(model_rf, type=1) |
|
1 2 3 4 |
## %IncMSE ## scrRate 34.81015 ## musRate 27.72078 ## actRate 59.58741 |
Usuwamy musRate:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
model_rf <- randomForest(filmRate ~ scrRate + actRate, means_train_df, type = "regression", ntree = 500, importance = TRUE) means_test_df$predRate_rf <- predict(model_rf, newdata = means_test_df[,2:6]) SS_res_rf <- sum((means_test_df$filmRate - means_test_df$predRate_rf)^2) R2_rf_3 <- 1 - SS_res_rf/SS_tot AdjR2_rf_3 <- 1 - (1-R2_rf)*(nrow(means_test_df)-1)/(nrow(means_test_df)-2-1) MSE_rf_3 <- SS_res_rf/nrow(means_test_df) |
Otrzymujemy nowe współczynniki, wstawmy je od razu do tabeli, w której porównamy wszystkie przygotowane wersje modelu random forest:
| Współczynnik | Model 1: | Model 2: | Model 3: | Model 4: |
|---|---|---|---|---|
| Użyte zmienne: | dirRate + scrRate + musRate + photoRate + actRate | dirRate + scrRate + musRate + actRate | scrRate + musRate + actRate | scrRate + actRate |
| R2 | 0.8954855 | 0.8948707 | 0.891335 | 0.8818369 |
| adj R2 | 0.8949598 | 0.8950654 | 0.8951707 | 0.8952759 |
| MSE | 0.1035868 | 0.1041962 | 0.1077005 | 0.1171143 |
Można by było przygotować jeszcze jeden model, tym razem z jedną zmienną. Ale jaki to ma sens?
Co widzimy w tabeli? Która wersja modelu jest najlepsza?
Dla R2 i adjR2 szukamy wartości najbliższych jedynki, zaś dla MSE najmniejszych. Różnice są niewielkie i trzeba wytężyć wzrok. Ułatwiłem Wam to wyróżniając stosowne wartości powyżej.
Zobaczmy jeszcze na wykresie (analogicznym do tego porównującego różne metody) zestawienie kolejnych wersji modelu opartego na random forest. Kolory dla poszczególnych modeli to kolejno:
- Model 1 = pomarańczowy
- Model 2 = zielony
- Model 3 = niebieski
- Model 4 = czerwony
- gruba linia – wartości prawdziwe
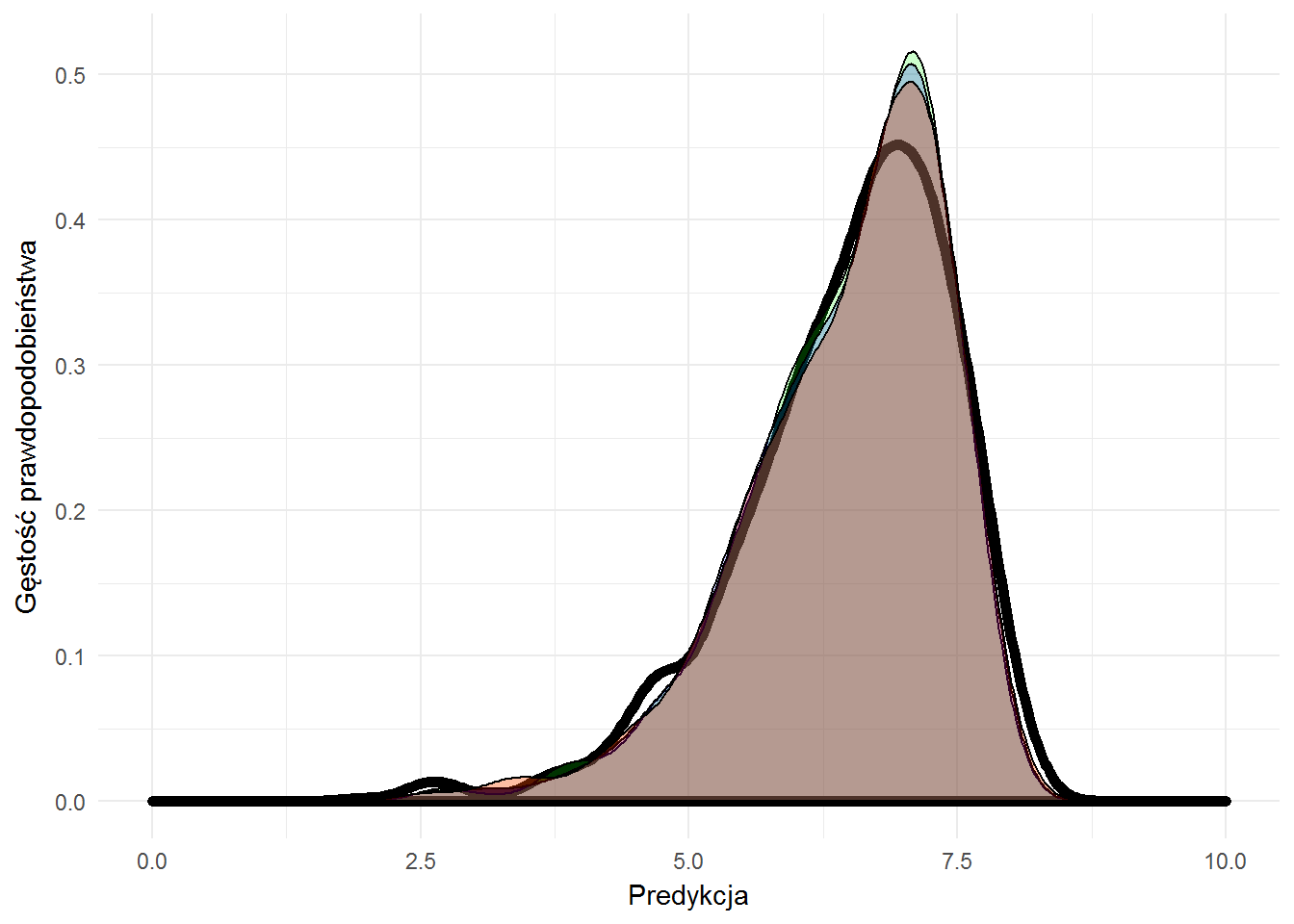
Prawda jest taka, że różnice są niezauważalne i niewiele tutaj widać. Trzeba zdać się na intuicję i doświadczenie (albo tak zwane potrzeby biznesowe). Model można jeszcze uzupełnić (ne etapie zbierania danych – funkcje PersonMean() oraz MovieMakersMean() trzeba odpowiednio zmodyfikować) o rok produkcji filmu oraz o odcięcie późniejszych filmów przy liczeniu średnich dla poszczególnych twórców.
Ze wskaźników wychodzi, że nalepsze są modele 1 i 4. Pierwszy bierze pod uwagę wszystkich twórców filmu, drugi (numer 4) – tylko scenariusz i aktorów. I trochę ten drugi model ma racji, o ile można tak powiedzieć. Laik ocenia to co widzi na ekranie – historię i jak bardzo wiarygodni są aktorzy w swoich rolach. Zdjęcia są dla smakoszy, reżyseria to delikatna sprawa – jak jest spieprzona to coś w odbiorze filmu nie gra (ale jak gra w nim boski Leo czy inny ulubieniec to nie ma to znaczenia), ale jeśli jest wszystko dobrze to jest niezauważalna.
Osobiście postawiłbym na model 1. Sam kiedyś chciałem reżyserować, a poza tym 2/3 lepszych wskaźników niż w modelu 4.
Podobało się? Zostaw komcia, daj lajka i poślij linka w świat (“odsłony, misiu, odsłony!”).
Wrzuciłem dane, które były wykorzystane w obliczeniach. Niestety pochodzą z innego komputera, na którym powstał wpis więc mogą być jakieś braki lub błędy, a kolumny mogą być błędnie nazwane… na początek lepsze to niż ściąganie wszystkiego raz jeszcze :)
Plik *.Rdata ma około 42 MB, znajduje się w archiwum
Po przenosinach na nowy serwer zmieni się adres archiwum – paczka leży tutaj http://prokulski.science/blog_iframes/filmweb_data.zip
Dzięki za ciekawy wpis!
Tak z ciekawości, w jakich kursach na Udemy Pan uczestniczył?
Tylko w jednym i szczerze mówiąc to bardziej dla uporządkowania wiedzy zgromadzonej z blogów czy też doświadczeń. Ale polecam https://www.udemy.com/machinelearning/learn/v4/
Super, akurat jest promocja na kursy Udemy :)
Chyba wykorzystam ten model, ale dla liczenia rekomendacji dla mnie. Wiem, że napisałeś też wpis o rekomendacjach, ale oparłeś je na ocenach podobnych użytkowników.
Super, super. Więcej się dowiedziałem z tego artykułu, aniżeli z kilku „mądrych” książek. Wielkie dzięki.