Dzisiaj wpis gościnny – autorstwa Dominiki Kuc. Opublikowałem na Dane i Analizy link do danych z zaproszeniem do skorzystania z nich. We wpisie na fanpage’u napisałem też, że jeśli ktoś zechce to mogę go opublikować tutaj. Dominika skorzystała i przygotowała analizę. Widzicie jak łatwo?
A teraz oddaję już miejsce na Waszych ekranach Dominice.
Przedmiot mojej analizy stanowi zanonimizowana próbka danych udostępniona przez Narodowy Fundusz Zdrowia dotycząca wystąpowania udaru niedokrwiennego mózgu. Więcej informacji na ten temat oraz dane znajdziemy pod TYM adresem.
Zbiór danych dotyczy świadczeń i leków refundowanych na rzecz pacjentów, spośród których u pewnego odsetka wystąpił udar niedokrwienny mózgu. Dane o udarze dotyczącą kolejnych dwóch lat po zrealizowaniu recepty na lek.
Udar mózgu jest uważany za trzecią najczęstszą przyczynę zgonu i główny powód inwalidztwa osób dorosłych. Jak podaje Światowa Organizacja Udaru Mózgu (World Stroke Organization), na świecie 80 mln osób przeszło udar mózgu, a 50 mln z nich jest z jego powodu niepełnosprawnych. Ta organizacja ustanowiła Światowy Dzień Udaru Mózgu, który przypada na 29 października.
Rozróżnia się dwa rodzaje udarów – niedokrwienny i krwotoczny. Rocznie prawie 80 tys. Polaków doświadcza udaru niedokrwiennego, który stanowi 85 proc. przypadków udaru. Połowa osób, która przeżyje, zmaga się z niedowładami, zaburzeniami mowy i innych funkcji. Większość z nich musi być otoczona całodobową opieką dotyczącą wszelkich codziennych czynności. Eksperci podkreślają, że kluczowe dla rokowania w udarze mózgu jest właściwe rozpoznanie i szybka interwencja lekarska (źródło).
Dane NFZ rozdzielone są na 6 tabel. Tabela pacjenci zawiera dane określające, czy u danego pacjenta wystąpił udar niedokrwienny w analizowanym okresie dwóch lat. Mamy próbkę złożoną z 500000 pacjentów. Aby uzyskać informację na temat wieku pacjenta, płci oraz powiatu, w którym mieszka, możemy połączyć ją z tabelą parametry pacjentów. W celu identyfikacji powiatu, wykorzystamy dodatkowy plik „kody_teryt.txt”. Zawiera on identyfikację powiatów po kodach TERYT. Dzięki plikowi „Powiaty” w formacie shp będziemy mogli utworzyć wizualizację frakcji udarów w poszczególnych województwach. Pondato wykorzystamy plik „wojewodztwa.txt” aby podzielić dane według województw. Przy szukaniu przyczyn udaru weźmiemy pod uwagę wynagrodzenie brutto w danym powiecie (plik „wyn_brutto_2016_gus.txt”) oraz poziom zanieczyszczeń w powiecie (plik „zanieczyszczenia.txt”). Dane na temat pochodzą z Banku Danych Lokalnych.
Następne dwie tabele – świadczenia oraz procedury zawierają zanonimizowane dane. Pierwsza z nich kryje między innymi informację o produkcie jednostkowym. Na jego podstawie świadczeniobiorcy rozliczają się z płatnikiem. Jest on określony za pomocą jednorodnych grup pacjentów (JGP), jednakże jego format w tabeli został poddany procesowi anonimizacji i nie możemy zanalizować jego treści. Z kolei tabela procedury zawiera informacje o wykonanych procedurach medycznych, lecz kod procedury również jest zaszyfrowany. Tajemnicy nie stanowią dla nas informacje o zrealizowanych receptach na leki refundowane, zawarte w tabeli recepty. Po wciągnięciu dwóch dodatkowych plików, „ATC1.txt” oraz „ATC2.txt” możemy określić jakie to są leki wg klasyfikacji anatomiczno-terapetyczno-chemicznej (ATC). Ostatnia udostępniona tabela nazywa się rozpoznania i możemy z niej odczytać, czy udar mózgu był głównym rozpoznaniem choroby u danego pacjenta.
Paczka plików wykorzystana w analizie, zawierająca dane udostępnione przez GOV oraz dodatkowe pliki, jest do pobrania TUTAJ.
Zapraszam do lektury.
|
1 2 3 4 5 6 |
# wczytanie podstawowych bibliotek import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns %matplotlib inline |
|
1 2 |
pacjenci = pd.read_csv('pacjenci.csv',sep=';') pacjenci.head() |
| ID_PACJENTA | ROK_WZGL | TYDZIEN_UDARU | CZY_UDAR | |
|---|---|---|---|---|
| 0 | 9910 | NaN | NaN | False |
| 1 | 953308 | NaN | NaN | False |
| 2 | 936540 | NaN | NaN | False |
| 3 | 902346 | NaN | NaN | False |
| 4 | 894583 | NaN | NaN | False |
|
1 |
pacjenci.shape |
|
1 |
(500000, 4) |
Tabela pacjenci zawiera ID, które jest kluczem łączenia z innymi tabelami. W zbiorze danych mamy próbkę o wielkości 500000 obserwacji. Na początek zidentyfikuję u ilu pacjentów wystąpił udar, a następnie zbadam strukturę osób chorych.
|
1 |
pacjenci.groupby('CZY_UDAR')['CZY_UDAR'].count() |
|
1 2 3 4 |
CZY_UDAR False 497029 True 2971 Name: CZY_UDAR, dtype: int64 |
|
1 |
pacjenci['CZY_UDAR'].sum()/pacjenci.shape[0] |
|
1 |
0.005942 |
Udar rozpoznano u około 0.59% pacjentów, czyli 2971 osób.
Kolumna „Tydzień udaru” nie została opisana w danych. Mogę się domyślać, że jest to tydzień, w którym rozpoznano udar od momentu zrealizowania recepty, ale nie jest to potwierdzona informacja.
|
1 2 3 4 5 |
plt.figure(figsize = (8,15)) sns.countplot(y=pacjenci['TYDZIEN_UDARU'],palette='inferno') plt.ylabel('Tydzień') plt.xlabel('Ilość pacjentów') plt.title('W którym tygodniu rozpoznano udar?') |
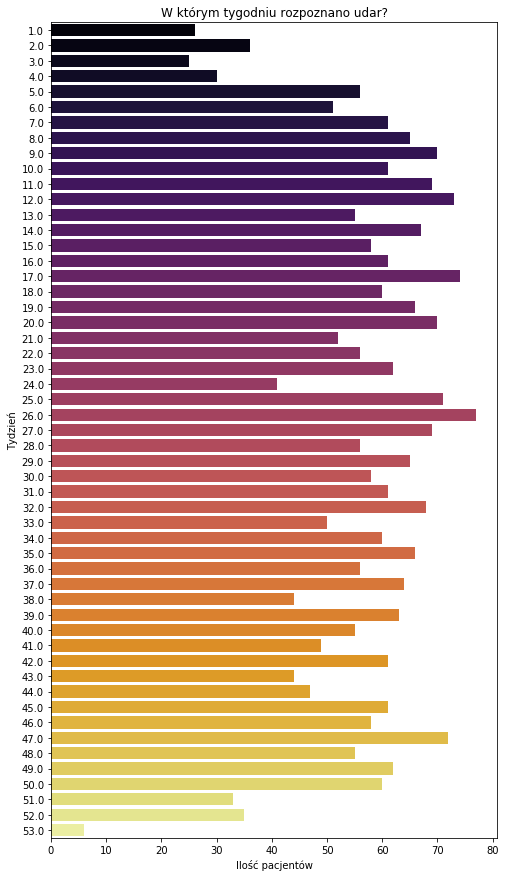
Udar najczęściej występował po 26 tygodniach, to jest około pół roku. W danych nie ma informacji o tym, czy pacjent zmarł. Z innych źródeł wiadomo, że pacjent ma duże szanse na wyleczenie, o ile trafi do szpitala do 4,5 godziny od wystąpienia udaru. To bardzo niewiele.
Kolumna „ROK_WZGL” nie została uwzględniona w opisie danych. Ciężko mi do niej odnieść, gdy nie wiem jakie informacje zawiera.
|
1 |
pacjenci.groupby('ROK_WZGL')['ROK_WZGL'].count() |
|
1 2 3 4 |
ROK_WZGL 0.0 1464 1.0 1507 Name: ROK_WZGL, dtype: int64 |
Przypuszczam, że są to informacje o tym, z którego roku są dane, ponieważ bierzemy pod uwagę dwa kolejne lata od momentu recepty. Załóżmy, że recepta została zrealizowana w 2016 roku. 0 może oznaczć, że upłynęło mniej niż rok, a 1 to ponad rok, ale nie więcej niż 2 lata.
Przejdźmy do kolejnej tabeli, która powie nam więcej o charakterystyce próbki.
|
1 2 |
parametry_pacjentow = pd.read_csv('parametry_pacjentow.csv',sep=';') parametry_pacjentow.head() |
| ID_PACJENTA | GRUPA_WIEKOWA | PLEC | TERYT_POWIATU | |
|---|---|---|---|---|
| 0 | 792137 | (73,78] | 2 | 2212.0 |
| 1 | 366964 | (38,43] | 2 | 2207.0 |
| 2 | 786905 | (63,68] | 1 | 2209.0 |
| 3 | 210416 | (23,28] | 2 | 2216.0 |
| 4 | 643866 | (58,63] | 1 | 2263.0 |
|
1 2 3 |
# połączenie dwóch tabel, każda kolejna będzie łączona w podobny sposób pacjenci_parametry = pd.merge(parametry_pacjentow, pacjenci, on='ID_PACJENTA', how='inner') pacjenci_parametry.head(2) |
| ID_PACJENTA | GRUPA_WIEKOWA | PLEC | TERYT_POWIATU | ROK_WZGL | TYDZIEN_UDARU | CZY_UDAR | |
|---|---|---|---|---|---|---|---|
| 0 | 792137 | (73,78] | 2 | 2212.0 | NaN | NaN | False |
| 1 | 366964 | (38,43] | 2 | 2207.0 | NaN | NaN | False |
|
1 |
pacjenci_parametry['CZY_UDAR'].isnull().any() |
|
1 |
False |
Upewnijmy się, że wszystkie informacje zostały porawnie połączone. Nie mamy pustych wierszy w kolumnie „CZY_UDAR”, więc wszystkich pacjentów z pierwszej tabeli można połączyć z tymi informacjami.
Zacznijmy od zbadania struktury płci w całej próbie.
|
1 |
pacjenci_parametry.groupby(['CZY_UDAR','PLEC'])['CZY_UDAR'].count() |
|
1 2 3 4 5 6 |
CZY_UDAR PLEC False 1 224886 2 272143 True 1 1360 2 1611 Name: CZY_UDAR, dtype: int64 |
Niestety opis danych nie zawiera informacji która wartość przypisana jest konkretnej płci, ale postaram się to wywnioskować. Pobieżnie patrząc w danych mamy więcej osób z udarem z grupy drugiej.
|
1 |
pacjenci_parametry[pacjenci_parametry['PLEC']==1]['CZY_UDAR'].sum()/len(pacjenci_parametry[pacjenci_parametry['PLEC']==1]) |
|
1 |
0.0060111559983380925 |
|
1 |
pacjenci_parametry[pacjenci_parametry['PLEC']==2]['CZY_UDAR'].sum()/len(pacjenci_parametry[pacjenci_parametry['PLEC']==2]) |
|
1 |
0.005884845518239003 |
Po bliższym przyjrzeniu się danym widzimy, że w grupie 1 udar występuje nieco częściej. Stwierdzam to na podstawie danej ilości osób u których wystąpił udar podzielonej przez całą wielkość grupy.
|
1 2 3 4 5 6 7 8 9 |
order_wiek = ['[18,23]', '(23,28]', '(28,33]', '(33,38]', '(38,43]', '(43,48]', '(48,53]', '(53,58]', '(58,63]', '(63,68]', '(68,73]', '(73,78]', '(78,83]', '(83,88]', '(88,93]', '(93,98]', '(98,103]','(103,108]' ] plt.figure(figsize = (16,5)) sns.countplot(pacjenci_parametry['GRUPA_WIEKOWA'],order=order_wiek,color='#410967') plt.xlabel('Grupa wiekowa') plt.ylabel('Ilosć osób') plt.title('Wiek pacjentów') |
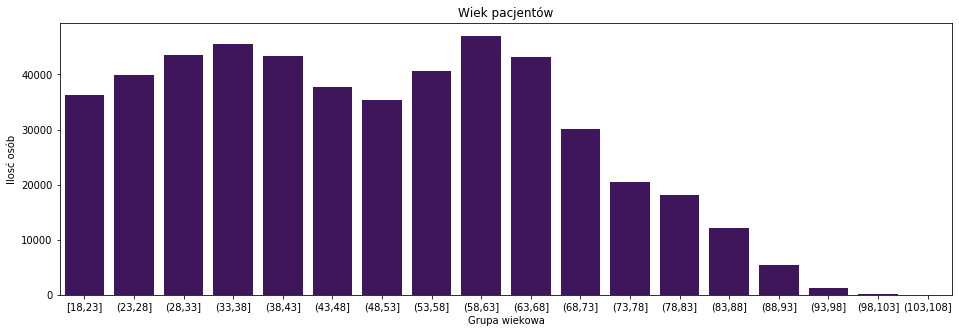
Tak prezentuje się rozkład wieku w próbce. Mamy dokładność co 5 lat. Widać dwa piki. Podzielmy te dane według płci.
|
1 2 3 4 5 |
plt.figure(figsize = (16,5)) sns.countplot(pacjenci_parametry['GRUPA_WIEKOWA'],hue=pacjenci_parametry['PLEC'],order=order_wiek,palette=['#DC5039','#FBA40A']) plt.xlabel('Grupa wiekowa') plt.ylabel('Ilosć osób') plt.title('Wiek pacjentów') |
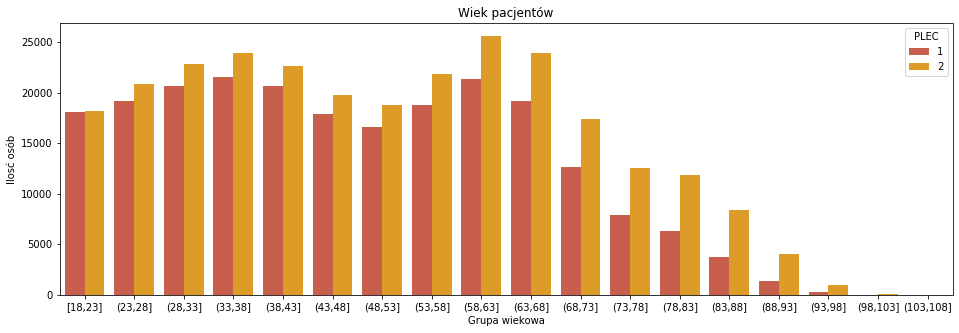
Po podziale wedłgu płci dalej mamy rozkłady bimodalne, ale każdy z nich ma nieco inny kształt. Na podstawie tego wykresu stwierdzam, że płeć 2 (kolor niebieski) to kobiety, ponieważ powszechnie wiadomo, że żyją one dłużej niż mężczyźni. Ale może być to też związane ze strukturą próbki, akurat tacy pacjenci zostali uwzględnieni w danych.
Skoncetrujmy się na tym 0.59% dobserwacji, u których wystąpił udar.
|
1 2 3 4 5 |
plt.figure(figsize = (16,5)) sns.countplot(pacjenci_parametry[pacjenci_parametry['CZY_UDAR']==True]['GRUPA_WIEKOWA'],order=order_wiek,color='#932567') plt.xlabel('Grupa wiekowa') plt.ylabel('Ilość') plt.title('Wiek pacjentów u których wystąpił udar mózgu') |
Dodając czynnik płci wyraźnie widać, że nasz rozkład bimodalny to tak naprawdę dwa rozkłady. U płci pierwszej najczęstszy przedział wiekowy to (63,68], z kolei u płci drugiej jest to (78,83]. Czy na pewno są to kobiety? Z zamieszczonego niżej źródła czytamy, że „Stosunek wiek/płeć wygląda następująco: 18 – 45 – częściej chorują kobiety, 45 – 70 – częściej chorują mężczyźni, >70 – prawdopodobieństwo wyrównuje się”. Jednakże suma sumarum kobiety żyją przeciętnie dłużej, więc pozostaję przy hipotezie, że płeć 2 to kobiety (źródło).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
g = pacjenci_parametry[pacjenci_parametry['PLEC']==1].groupby('GRUPA_WIEKOWA')['GRUPA_WIEKOWA'].count() g1 = pacjenci_parametry[(pacjenci_parametry['CZY_UDAR']==True) & (pacjenci_parametry['PLEC']==1)].groupby('GRUPA_WIEKOWA')['GRUPA_WIEKOWA'].count() g2 = pacjenci_parametry[pacjenci_parametry['PLEC']==2].groupby('GRUPA_WIEKOWA')['GRUPA_WIEKOWA'].count() g3 = pacjenci_parametry[(pacjenci_parametry['CZY_UDAR']==True) & (pacjenci_parametry['PLEC']==2)].groupby('GRUPA_WIEKOWA')['GRUPA_WIEKOWA'].count() df = pd.concat([g.rename('plec1_all'),g1.rename('plec1_udar'),g2.rename('plec2_all'),g3.rename('plec2_udar')],axis=1,sort=True).fillna(0) df = df.reindex(order_wiek).reset_index() df['procent_1']=df['plec1_udar']/df['plec1_all'] df['procent_2']=df['plec2_udar']/df['plec2_all'] plt.figure(figsize = (16,5)) plt.plot(df['index'],df['procent_1'],color='#DC5039',label='Plec 1') plt.plot(df['index'],df['procent_2'],color='#FBA40A',label='Plec 2') plt.legend(loc='best') plt.xlabel('Wiek') plt.ylabel('Odsetek pacjentów') plt.title('Odsetek udarowców względem wieku') |
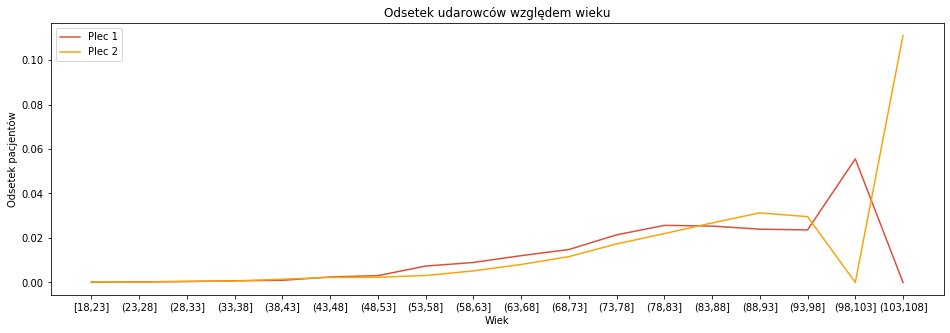
Zamiast liczebności na wykresie pokazałam odsetek pacjentów mających udar, każda płeć to osobna krzywa. Wartości na osi Y można traktować jako prawdopdobieństwo, że osoba w danym wieku będzie mieć udar. Widzimy, że ryzyko w młodym wieku jest podobne, później mamy przewagę płci 1, a następnie, w okolicach 85 lat proporcje wyrównują się, żeby potem płeć 2 przewyższyła płeć 1. Prawa strona wykresu jest nieco zadziwiająca, podejrzyjmy ramkę danych by zobaczyć dokładną strukturę udarów w tej kategorii wiekowej.
|
1 |
df.tail() |
| index | plec1_all | plec1_udar | plec2_all | plec2_udar | procent_1 | procent_2 | |
|---|---|---|---|---|---|---|---|
| 13 | (83,88] | 3748 | 95.0 | 8441 | 226.0 | 0.025347 | 0.026774 |
| 14 | (88,93] | 1336 | 32.0 | 3997 | 125.0 | 0.023952 | 0.031273 |
| 15 | (93,98] | 254 | 6.0 | 1014 | 30.0 | 0.023622 | 0.029586 |
| 16 | (98,103] | 18 | 1.0 | 84 | 0.0 | 0.055556 | 0.000000 |
| 17 | (103,108] | 1 | 0.0 | 18 | 2.0 | 0.000000 | 0.111111 |
W celu wyciągnięcia informacji o powiecie, z którego pochodzi dana obserwacja dodałam tabelę z identyfikacją kodów TERYT.
|
1 2 3 4 |
teryt = pd.read_csv('kody_teryt.txt',header=0,sep="\t") teryt.columns = ['Powiat','TERYT_POWIATU'] teryt['TERYT_POWIATU']= teryt['TERYT_POWIATU'].str.replace(' ', '') teryt.head(2) |
| Powiat | TERYT_POWIATU | |
|---|---|---|
| 0 | aleksandrowski | 0401 |
| 1 | augustowski | 2001 |
|
1 2 3 4 |
teryt['TERYT_POWIATU'] = teryt['TERYT_POWIATU'].astype('int64') p = pd.merge(teryt, pacjenci_parametry, on='TERYT_POWIATU', how='inner') powiaty = p[p['CZY_UDAR']==True].groupby('Powiat')['Powiat'].count().sort_values(ascending=False) powiaty.iloc[:10,] |
|
1 2 3 4 5 6 7 8 9 10 11 12 |
Powiat m. Warszawa 111 m. Łódź 76 m. Kraków 44 m. Poznań 42 m. Bydgoszcz 37 m. Gdańsk 36 m. Lublin 36 m. Częstochowa 35 m. Szczecin 35 m. Wrocław 31 Name: Powiat, dtype: int64 |
To są powiaty z najwększą ilością pacjentów, którzy mieli udar. Lecz bardziej interesująca będzie frakcja w powiatach, czyli ilość osób chorych na udar w danym powiecie podzielona przez ilość wszystkich osób.
| Ilość osób | Ilość osób z udarem | Frakcja | |
|---|---|---|---|
| Powiat | |||
| aleksandrowski | 706 | 7.0 | 0.009915 |
| augustowski | 756 | 3.0 | 0.003968 |
| bartoszycki | 833 | 4.0 | 0.004802 |
| bełchatowski | 1580 | 7.0 | 0.004430 |
| bialski | 1591 | 9.0 | 0.005657 |
|
1 |
p4['Frakcja'].sort_values(ascending=False).iloc[:10,] |
|
1 2 3 4 5 6 7 8 9 10 11 12 |
Powiat biłgorajski 0.017075 świebodziński 0.015605 jarosławski 0.015404 żyrardowski 0.014558 m. Jaworzno 0.014252 tomaszowski (lubelski) 0.013934 złotoryjski 0.013761 sztumski 0.013514 pajęczański 0.013025 krasnostawski 0.012889 Name: Frakcja, dtype: float64 |
Tutaj są powiaty z największą frakcją osób, które mają udar. Warszawa juz nie jest wśród tych najwyższych. Zwizualizuję te dane na mapie geograficznej. W tym celu musimy doinstalować dodatkowe biblioteki oraz wczytać plik shp, który ma zdefiniowane współrzędne geograficzne.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
import geopandas import descartes powiaty_shp = geopandas.read_file("Powiaty/Powiaty.shp") p['TERYT_POWIATU'] = [str(x).zfill(4) for x in p['TERYT_POWIATU']] powiaty_shp['TERYT_POWIATU'] = powiaty_shp['JPT_KOD_JE'] t = p.groupby('TERYT_POWIATU') powiaty_shp['Ilość osób'] = powiaty_shp['TERYT_POWIATU'].map(t['TERYT_POWIATU'].count()) powiaty_shp['Ilość udarów'] = powiaty_shp['TERYT_POWIATU'].map(t['CZY_UDAR'].sum()) powiaty_shp['Frakcja'] =powiaty_shp['Ilość udarów'] / powiaty_shp['Ilość osób'] col = 'Frakcja' fig, ax = plt.subplots(figsize = (15, 12)) powiaty_shp.plot(ax=ax, column=col, cmap='inferno',edgecolor='white',linewidth=0.2,legend=True) ax.set_axis_off() plt.title('Frakcja występowania udarów w powiatach') plt.show() |
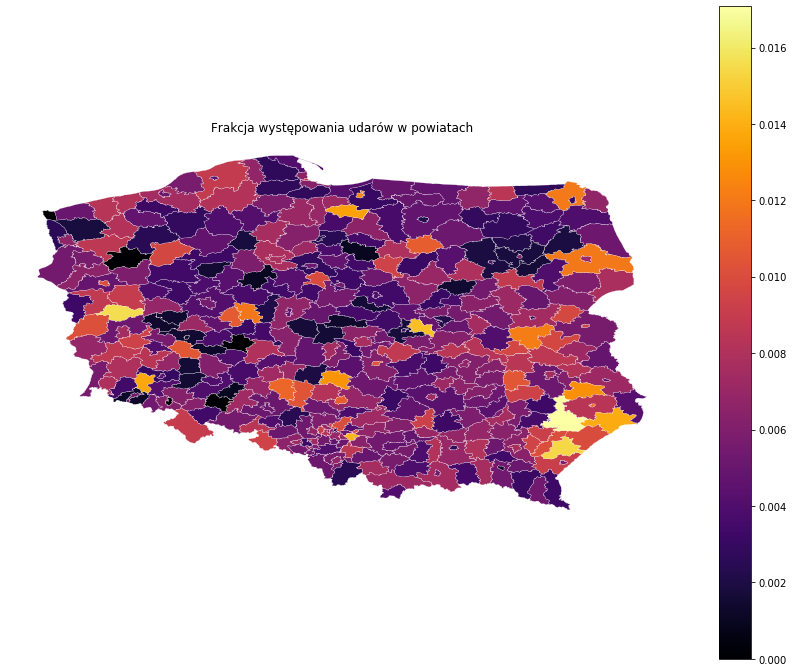
Dodam jeszcze województwo.
|
1 2 3 4 5 6 7 8 |
woj = pd.read_csv('wojewodztwa.txt',sep="\t") wojewodztwa = pd.merge(p4, woj, on='Powiat', how='inner') plt.figure(figsize = (16,7)) sns.boxplot(x='Województwo', y='Frakcja', data=wojewodztwa,palette='inferno') plt.xticks(rotation='vertical') plt.xlabel('Województwa') plt.ylabel('Frakcja udarów') plt.title('Frakcja udarów w poszczególnych województwach') |
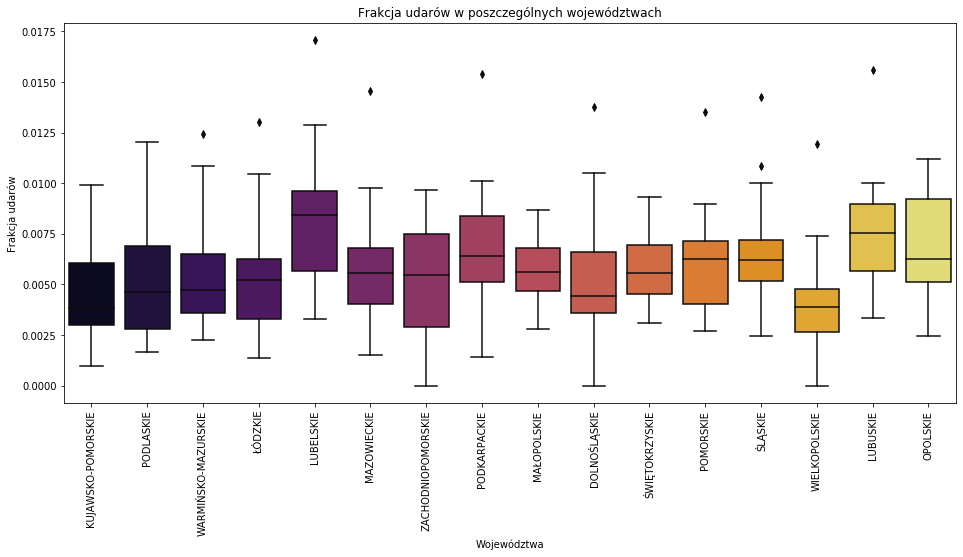
Prawie w każdym województwie mamy jakieś powiaty z wartością odstającą. Najmniejniej chorych pacjentów jest w województwie wielkopolskim, natomiast nawięcej w lubelskim.
Zestawmy dane o frakcji osób w powiatach z przeciętnym miesięcznym wynagrodzeniem brutto. Dane na ten temat pochodzą z BDL, jako rok odniesienia przyjęłam 2016, jednakże nie mam pewności, że ten sam okres występuje w danych z NFZ. Będę porównywać wielkość wynagrodzenia, w danych mam uwzględniony jeszcze stosunek do średniej krajowej (Polska=100), ale będę korzystać z ostatniej kolumny.
|
1 2 3 |
wynagrodzenie = pd.read_csv('wyn_brutto_2016_gus.txt',sep="\t",decimal=',') wynagr = pd.merge(wojewodztwa, wynagrodzenie, on='Powiat', how='inner') wynagr.head() |
| Powiat | Ilość osób | Ilość osób z udarem | Frakcja | Województwo | Kod | wyn_stosunek_do_średniej_krajowej | wynagrodzenie | |
|---|---|---|---|---|---|---|---|---|
| 0 | aleksandrowski | 706 | 7.0 | 0.009915 | KUJAWSKO-POMORSKIE | 401000 | 73.9 | 3170.04 |
| 1 | augustowski | 756 | 3.0 | 0.003968 | PODLASKIE | 2001000 | 89.0 | 3816.77 |
| 2 | bartoszycki | 833 | 4.0 | 0.004802 | WARMIŃSKO-MAZURSKIE | 2801000 | 80.4 | 3449.70 |
| 3 | bełchatowski | 1580 | 7.0 | 0.004430 | ŁÓDZKIE | 1001000 | 134.7 | 5778.97 |
| 4 | bialski | 1591 | 9.0 | 0.005657 | LUBELSKIE | 601000 | 74.2 | 3184.04 |
|
1 2 3 4 5 6 7 8 9 10 |
from scipy import stats def r2(x, y): return stats.pearsonr(x, y)[0] ** 2 plt.figure(figsize = (16,8)) sns.jointplot('Frakcja','wynagrodzenie',data=wynagr, kind="reg", stat_func=r2,color='#410967') plt.xlabel('Frakcja osób z udarem mózgu') plt.ylabel('Przeciętne wynagrodzenie (log)') plt.title('Zależność między zjawiskiem udaru mózgu a przeciętnym wynagrodzeniem w powiatach',pad=100) |
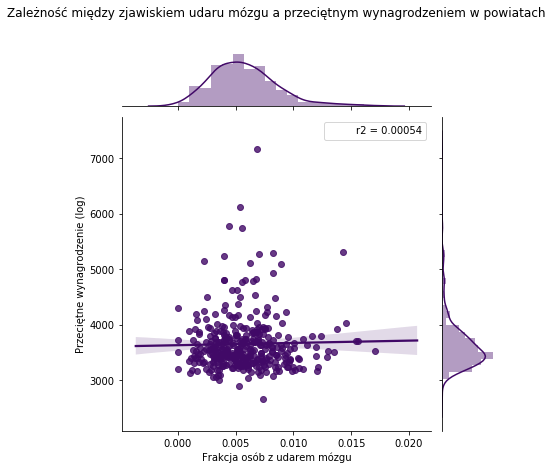
Przeciętne wynagrodzenia nie jest związane z częstością udaru mózgu. Widać to na wykresie – linia regresji nie jest zbyt dopasowana do danych. Policzenie mało istotnego R^2 było tylko rozrywką.
|
1 2 3 4 5 6 7 |
plt.figure(figsize = (15,5)) sns.scatterplot('Frakcja','wynagrodzenie',hue='Województwo',data=wynagr,palette='inferno') plt.xlabel('Frakcja osób z udarem mózgu') plt.ylabel('Przeciętne wynagrodzenie') plt.title('Zależność między zjawiskiem udaru mózgu a przeciętnym wynagrodzeniem w województwach') plt.legend(loc='best', bbox_to_anchor=(1,1),ncol=1) plt.xlim((0,0.020)) |
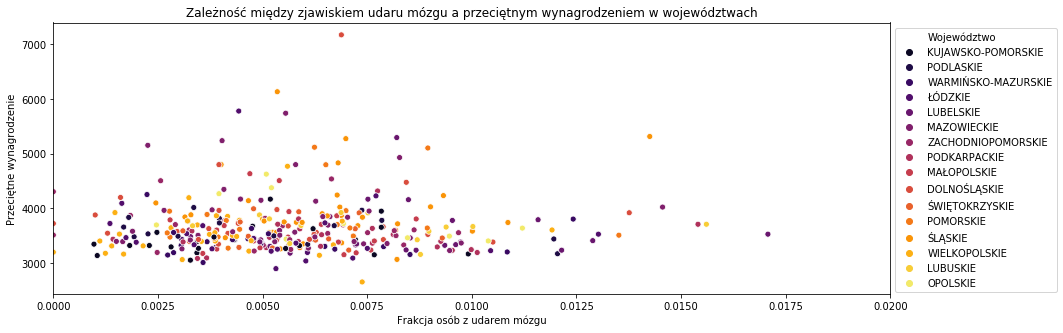
Przy podziale danych wedłuch województw również brak widocznych zależności.
Może poziom zanieczyszczeń powie nam coś więcej o nieoczywistych przyczynach udaru?
|
1 2 3 |
zanieczyszczenie = pd.read_csv('zanieczyszczenie.txt',sep="\t",decimal=',') zan = pd.merge(wojewodztwa, zanieczyszczenie, on='Powiat', how='inner').dropna() zan.head() |
| Powiat | Ilość osób | Ilość osób z udarem | Frakcja | Województwo | Kod | Zanieczyszczenie | |
|---|---|---|---|---|---|---|---|
| 0 | aleksandrowski | 706 | 7.0 | 0.009915 | KUJAWSKO-POMORSKIE | 401000 | 0.05 |
| 1 | augustowski | 756 | 3.0 | 0.003968 | PODLASKIE | 2001000 | 0.01 |
| 2 | bełchatowski | 1580 | 7.0 | 0.004430 | ŁÓDZKIE | 1001000 | 0.85 |
| 3 | bialski | 1591 | 9.0 | 0.005657 | LUBELSKIE | 601000 | 0.01 |
| 4 | białobrzeski | 469 | 4.0 | 0.008529 | MAZOWIECKIE | 1401000 | 0.02 |
|
1 2 3 4 5 6 7 |
plt.figure(figsize = (15,5)) sns.scatterplot('Frakcja','Zanieczyszczenie',hue='Województwo',data=zan,palette='inferno') plt.legend(loc='best', bbox_to_anchor=(1,1),ncol=1) plt.xlabel('Frakcja osób z udarem mózgu') plt.ylabel('Poziom zanieczyszczenia') plt.xlim((0,0.020)) plt.title('Poziom zanieczyszczeń w powiatach a częstotliwość udarów') |
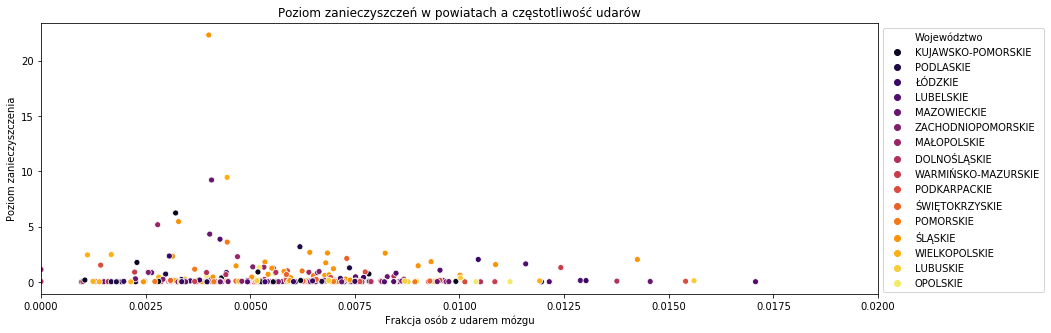
Tutaj również nie widzimy żadnej zależności. Moim zdaniem nasza próbka jest zbyt mało liczna, aby doszukiwać się takich zależności. Frakcje w powiatach różnią się dopiero na którymś miejscu po przecinku, więc na podstawie powiatów i informacji o nich ciężko określić przyczyny udarów.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
a1 = p[p['PLEC']==1].groupby('Powiat')['Powiat'].count() a2 = p[p['PLEC']==2].groupby('Powiat')['Powiat'].count() a3 = p[(p['PLEC']==1) & (p['CZY_UDAR']==True)].groupby('Powiat')['Powiat'].count() a4 = p[(p['PLEC']==2) & (p['CZY_UDAR']==True)].groupby('Powiat')['Powiat'].count() df2 = pd.concat([a1.rename('plec1_all'),a3.rename('p1_udar'),a2.rename('plec2_all'),a4.rename('p2_udar')],axis=1,sort=True) df2['Plec 1']=df2['p1_udar']/df2['plec1_all'] df2['Plec 2']=df2['p2_udar']/df2['plec2_all'] names = p4['Frakcja'].sort_values(ascending=False).iloc[:20,].index df = df2.T plt.figure(figsize = (20,4)) sns.heatmap(df[names].loc[['Plec 1','Plec 2']]) plt.xlabel('Powiaty') plt.ylabel('Płeć') plt.xticks(rotation=75) plt.title('Odsetek osób z udarem mózgu w podziale na płeć - powiaty z największą frakcją') |

Na heatmapie widać powiaty z największą frakcją z podziałem na płeć. Skala to odsetek udarów w danym powiecie.
Następna zanalizowana tabela zawiera informację o udzielnych świadczeniach.
|
1 2 |
swiadczenia = pd.read_csv('swiadczenia.csv',sep=';') swiadczenia.head() |
| ID_PACJENTA | ID_EPIZODU | ID_KONTAKTU | ID_KSIEGI_GLOWNEJ | ROK_SWIADCZENIA | TYDZIEN_POCZATKU_KONTAKTU | TYDZIEN_KONCA_KONTAKTU | KOD_ZAKRESU | KOD_PRODUKTU_JEDNOSTKOWEGO | TYP_KOMORKI | RODZAJ_SWIADCZEN | KWOTA_ROZLICZONA | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 21466 | 55625667 | 20359413 | NaN | -2 | 2 | 2.0 | 1506110 | 5.01.00.0030856 | 16 | PODSTAWOWA OPIEKA ZDROWOTNA | 0 |
| 1 | 197685 | 84652115 | 98978481 | NaN | -2 | 2 | 2.0 | 1506110 | 5.01.00.0030856 | 16 | PODSTAWOWA OPIEKA ZDROWOTNA | 0 |
| 2 | 21466 | 13879209 | 82087452 | NaN | -2 | 3 | 3.0 | 1506110 | 5.01.00.0030856 | 16 | PODSTAWOWA OPIEKA ZDROWOTNA | 0 |
| 3 | 372836 | 46476951 | 43672487 | NaN | -2 | 1 | 1.0 | 1506110 | 5.01.00.0030856 | 3010 | PODSTAWOWA OPIEKA ZDROWOTNA | 0 |
| 4 | 845904 | 87283796 | 28396473 | NaN | -2 | 1 | 1.0 | 1506110 | 5.01.00.0030856 | 3010 | PODSTAWOWA OPIEKA ZDROWOTNA | 0 |
Kod zakresu, kod produktu jednostkowego oraz typ komórki zostały zanonimozowane. Nie da się wyciągnać z nich żadnej informacji (a przynajmniej nie tak łatwo jak z reszty danych).
Możemy sprawdzić rodzaj świadczeń i kwotę rozliczoną.
|
1 2 |
p_swiadczenia = pd.merge(p, swiadczenia, on='ID_PACJENTA', how='inner') p_swiadczenia.groupby(['CZY_UDAR','RODZAJ_SWIADCZEN'])['RODZAJ_SWIADCZEN'].count() |
|
1 2 3 4 |
CZY_UDAR RODZAJ_SWIADCZEN False PODSTAWOWA OPIEKA ZDROWOTNA 1033915 True PODSTAWOWA OPIEKA ZDROWOTNA 10365 Name: RODZAJ_SWIADCZEN, dtype: int64 |
|
1 |
p_swiadczenia.groupby(['CZY_UDAR'])['KWOTA_ROZLICZONA'].sum() |
|
1 2 3 4 |
CZY_UDAR False 4 True 0 Name: KWOTA_ROZLICZONA, dtype: int64 |
Rodzaj świadczeń jest wszędzie taki sam. Jest to podstawowa opieka zdrowotna. Kwota rozliczona prawie wszędzie jest równa zero. Te kolumny nie są zbyt interesujące.
Grupowanie możemy przeprowadzić również po ID. Najpierw sprawdzimy ile pacjentów występowało o świadczenia więcej niż raz.
|
1 |
len(swiadczenia.loc[swiadczenia.groupby('ID_PACJENTA')['ID_EPIZODU'].count().values>1]) |
|
1 |
231811 |
A ile spośród nich miało udar?
|
1 2 |
s = p_swiadczenia.loc[p_swiadczenia.groupby('ID_PACJENTA')['ID_EPIZODU'].count().values>1] s.groupby('CZY_UDAR')['CZY_UDAR'].count() |
|
1 2 3 4 |
CZY_UDAR False 228399 True 2459 Name: CZY_UDAR, dtype: int64 |
Okazuje się, że 1,08% miało udar. Są to proporcje podobne jak w całej próbce danych.
Przedstawię teraz liczbę świadczeń pacjentów z udarem w podziale na ich wiek i płeć.
|
1 2 3 4 5 6 7 8 |
wiek_swiadczenia = pd.DataFrame(p_swiadczenia.groupby(['GRUPA_WIEKOWA','CZY_UDAR'])['ID_PACJENTA'].count()) wiek_swiadczenia.reset_index(inplace=True) plt.figure(figsize = (16,5)) sns.countplot(p_swiadczenia[p_swiadczenia['CZY_UDAR']==True]['GRUPA_WIEKOWA'], order=order_wiek, palette=['#DC5039','#FBA40A'], hue=p_swiadczenia['PLEC']) plt.xlabel('Wiek') plt.ylabel('Liczba świadczeń') plt.title('Liczba świadczeń pacjentów z udarem w zależności od wieku i płci') |
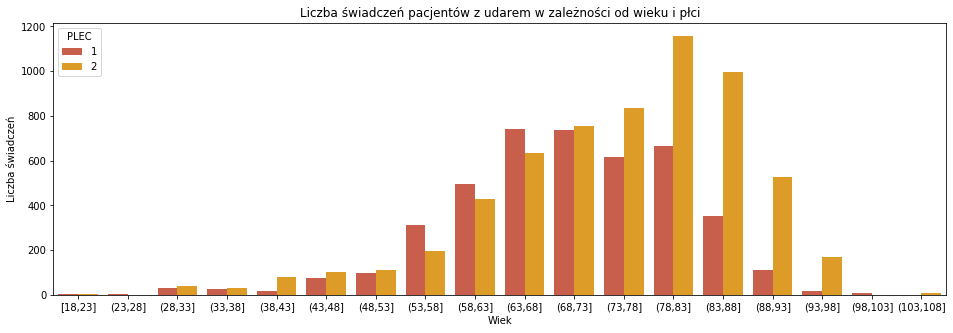
Rozkład wygląda podobnie jak ogólny rozkład wieku osób z udarem mózgu. Starsi pacjenci, u których wystąpił udar pobierali więcej świadczeń niż młodsi, ale nie doszukiwałabym się tutaj dużej zależności – po prostu jest ich analogicznie więcej w danych.
Pogrupujmy dane według ID Pacjenta oraz ID Epizodu, a następnie policzmy ilości epizodów dla tak pogrupowanych danych. Interesujące będą ilości większe niż 1.
|
1 2 |
s2 = p_swiadczenia.loc[p_swiadczenia.groupby(['ID_PACJENTA','ID_EPIZODU'])['ID_EPIZODU'].count().values>1] s2.groupby('CZY_UDAR')['CZY_UDAR'].count() |
|
1 2 3 4 |
CZY_UDAR False 837 True 8 Name: CZY_UDAR, dtype: int64 |
Pacjenci, którzy mieli więcej niż jeden epizod związany z tym samym ID w większości nie mieli udaru, jak pokazuje powyższa tabelka. Tabela Procedury jest w całości zaszyfrowana.
|
1 2 |
procedury = pd.read_csv('procedury.csv',sep=';') procedury.head() |
| ID_EPIZODU | KOD_PROCEDURY | |
|---|---|---|
| 0 | 15079215 | 806.0 |
| 1 | 49779661 | 806.0 |
| 2 | 16963243 | 806.0 |
| 3 | 16963243 | 806.0 |
| 4 | 33131101 | 806.0 |
Kod procedury dawałby nam informację jakie badanie zostało wykonane przy tym epizodzie.
Przejdźmy do danych o receptach. Przy tych danych dodam kolumny które będą rozszyfrowywać kod ATC (w tym celu wciągnę dodatkowe pliki) i połączę wszystko po ID Pacjenta, tak jak to robiłam do tej pory. Pondato usunę kilka zbędnych kolumn.
|
1 2 3 4 5 |
recepty = pd.read_csv('recepty.csv',sep=';',decimal=',') ATC_code1 = pd.read_csv('ATC1.txt',sep='\t',header=None) ATC_code2 = pd.read_csv('ATC2.txt',sep='\t',header=None) ATC_code1.head() |
| 0 | 1 | |
|---|---|---|
| 0 | A | Przewód pokarmowy i metabolizm |
| 1 | B | Krew i układ krwiotwórczy |
| 2 | C | Układ sercowo-naczyniowy |
| 3 | D | Dermatologia |
| 4 | G | Układ moczowo-płciowy i hormony płciowe |
|
1 |
ATC_code2.head() |
| 0 | 1 | |
|---|---|---|
| 0 | A01 | Preparaty stomatologiczne |
| 1 | A02 | Leki stosowane w chorobach związanych z nadmie… |
| 2 | A03 | Leki stosowane w czynnościowych zaburzeniach p… |
| 3 | A04 | Leki przeciwwymiotne i przeciw nudnościom |
| 4 | A05 | Leki stosowane w chorobach dróg żółciowych i w… |
|
1 2 3 4 5 6 7 8 9 10 11 12 |
ATC_code1.columns = ['KROTKI_KOD_ATC','Name'] ATC_code2.columns = ['KOD_ATC','Full_name'] r = pd.merge(recepty, ATC_code2, on='KOD_ATC', how='inner') r['KROTKI_KOD_ATC'] = r['KOD_ATC'].str[:1] r2 = pd.merge(r, ATC_code1, on='KROTKI_KOD_ATC', how='inner') columns = ['TERYT_POWIATU','ROK_WZGL','ID_EPIZODU','ID_KONTAKTU','ID_KSIEGI_GLOWNEJ', 'KOD_PRODUKTU_JEDNOSTKOWEGO','TYP_KOMORKI','KOD_ZAKRESU','KWOTA_ROZLICZONA','RODZAJ_SWIADCZEN'] p_new = p_swiadczenia.drop(columns,axis=1) p_recepty = r2.drop(['ID_RECEPTY','KOD_ATC','KROTKI_KOD_ATC','ROK_REALIZACJI_RECEPTY','TYDZIEN_POCZATKU_REALIZACJI'],axis=1) p_all = pd.merge(p_recepty, p_new, on='ID_PACJENTA', how='inner') p_all.head() |
| ID_PACJENTA | LICZBA_OPAKOWAN | Full_name | Name | Powiat | GRUPA_WIEKOWA | PLEC | TYDZIEN_UDARU | CZY_UDAR | ROK_SWIADCZENIA | TYDZIEN_POCZATKU_KONTAKTU | TYDZIEN_KONCA_KONTAKTU | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 84791 | 1.0 | Leki działające na układ renina-angiotensyna | Układ sercowo-naczyniowy | radomszczański | (58,63] | 1 | NaN | False | -2 | 36 | 36.0 |
| 1 | 84791 | 1.0 | Leki działające na układ renina-angiotensyna | Układ sercowo-naczyniowy | radomszczański | (58,63] | 1 | NaN | False | -2 | 33 | 33.0 |
| 2 | 84791 | 1.0 | Leki działające na układ renina-angiotensyna | Układ sercowo-naczyniowy | radomszczański | (58,63] | 1 | NaN | False | -2 | 36 | 36.0 |
| 3 | 84791 | 1.0 | Leki działające na układ renina-angiotensyna | Układ sercowo-naczyniowy | radomszczański | (58,63] | 1 | NaN | False | -2 | 33 | 33.0 |
| 4 | 84791 | 1.0 | Leki działające na układ renina-angiotensyna | Układ sercowo-naczyniowy | radomszczański | (58,63] | 1 | NaN | False | -2 | 36 | 36.0 |
|
1 2 3 4 5 6 7 |
plt.figure(figsize = (16,5)) sns.countplot(p_all['Name'],palette=['#FBA40A','#932567'],hue=p_all['CZY_UDAR']) plt.xlabel('Kategorie leków') plt.yscale('log') plt.ylabel('Ilość osób (log)') plt.xticks(rotation=80) plt.title('Jakie leki najczęściej kupują pacjenci?') |
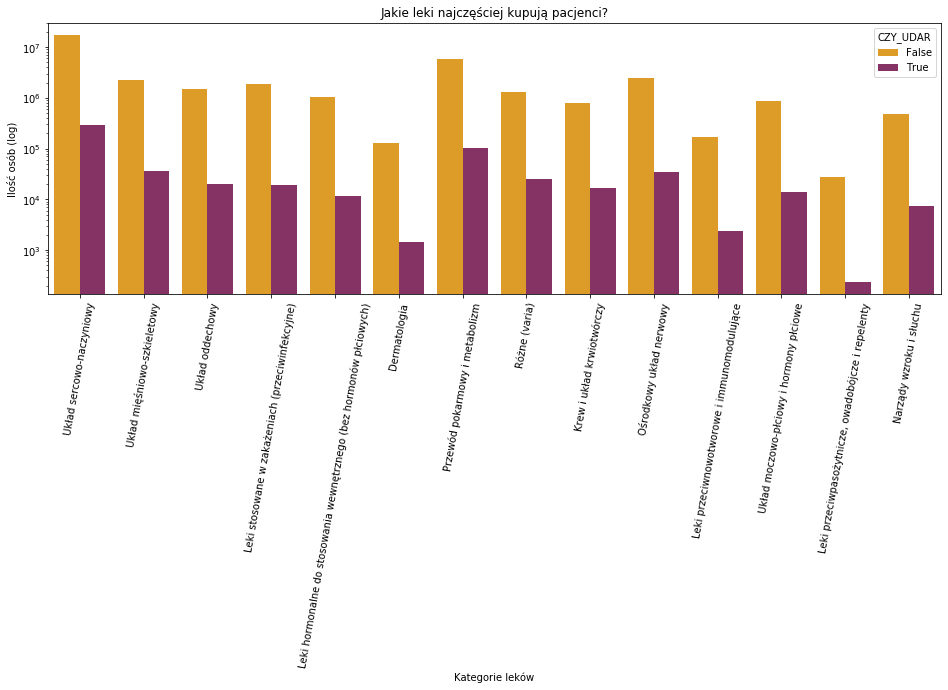
Takie mamy podstawowe kategorie recept. Wsród osób, które miały udar najczęściej występują recepty dotyczące układu sercowo-naczyniowego oraz przewodu pokarmowego i metabolizmu.
Kategorie leków mogą być bardziej szczegółowe.
|
1 |
p_all['Full_name'].nunique() |
|
1 |
84 |
Mamy 84 szczegółowych kategorii. Zidentyfikuję 10 najczęstszych dla całej próby oraz 10 najczęstszych dla udarowców.
|
1 |
p_all[p_all['CZY_UDAR']==True].groupby(['ID_PACJENTA','Full_name'])['LICZBA_OPAKOWAN'].count().sort_values(ascending=False)[:15] |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
ID_PACJENTA Full_name 310607 Leki przeciwzapalne i przeciwreumatyczne 1344 850102 Leki stosowane w chorobach obturacyjnych dróg oddechowych 902 818609 Leki stosowane w chorobach obturacyjnych dróg oddechowych 777 118753 Środki diagnostyczne 768 298451 Leki przeciwbakteryjne do stosowania wewnętrznego 760 594298 Leki stosowane w chorobach związanych z nadmierną kwasowością soku żołądkowego 756 646539 Leki moczopędne 744 Leki stosowane w cukrzycy 696 Leki stosowane w chorobach związanych z nadmierną kwasowością soku żołądkowego 696 Leki ?-adrenolityczne 696 594298 Antagonisty kanału wapniowego 672 646539 Leki urologiczne 648 362695 Leki stosowane w cukrzycy 629 594298 Leki przeciwdrgawkowe 588 298451 Leki przeciwbólowe 580 Name: LICZBA_OPAKOWAN, dtype: int64 |
|
1 |
p_all[p_all['CZY_UDAR']==False].groupby(['ID_PACJENTA','Full_name'])['LICZBA_OPAKOWAN'].count().sort_values(ascending=False)[:15] |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
ID_PACJENTA Full_name 582030 Psychoanaleptyki 36015 328086 Leki przeciwbólowe 15904 524876 Leki przeciwbólowe 5576 486139 Leki przeciwdrgawkowe 4914 Leki przeciwbólowe 4698 774853 Leki przeciwbólowe 3750 46185 Leki przeciwdrgawkowe 3560 192439 Antagonisty kanału wapniowego 3375 46185 Leki oftalmologiczne 3360 394654 Leki stosowane w chorobach obturacyjnych dróg oddechowych 3088 524876 Leki stosowane w chorobach związanych z nadmierną kwasowością soku żołądkowego 2870 779334 Leki przeciwbólowe 2844 262267 Leki przeciwbólowe 2738 46185 Leki stosowane w chorobach związanych z nadmierną kwasowością soku żołądkowego 2720 104606 Leki moczopędne 2475 Name: LICZBA_OPAKOWAN, dtype: int64 |
Grupując pacjentów po ID i patrząc na ilość opakowań leków, widzimy, że osoby które nie miały udaru zazwyczaj kupowały dużą ilość leków przeciwbólowych, zaś ci z udarem bardziej specjalistyczne.
|
1 2 3 4 5 6 7 |
opakowania = p_all[p_all['CZY_UDAR']==True].pivot_table(columns='GRUPA_WIEKOWA', index='Name', values='LICZBA_OPAKOWAN',aggfunc=lambda x: np.log(sum(x))) plt.figure(figsize = (18,10)) sns.heatmap(opakowania,linewidths=1,linecolor='white',cmap='inferno',xticklabels = order_wiek ) plt.xlabel('Wiek') plt.ylabel('Grupy leków') plt.title('Ilość opakowań zakupionych leków przez udarowców (skala logarytmiczna)') |
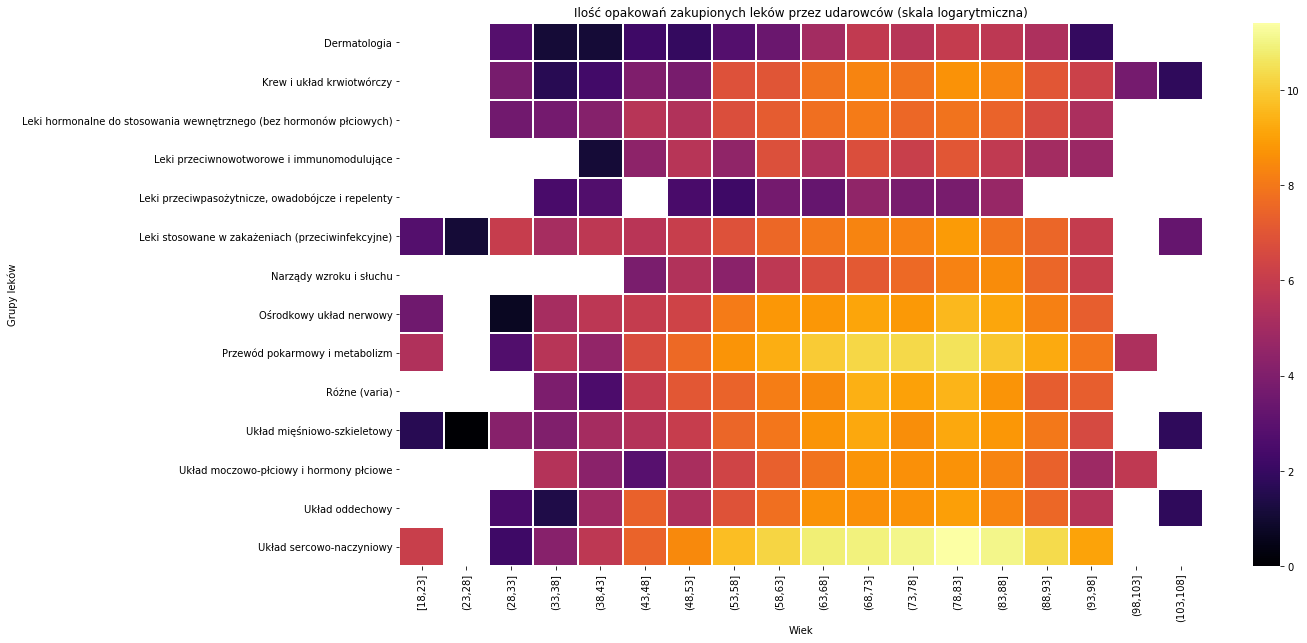
Na heatmapie wyraźnie wyróżniają się starsze grupy pacjentów, które kupują leki związane z układem sercowo-naczyniowym oraz przewodem pokarmowym i metabolizmem. Mamy też trochę pustych mejsc, co oznacza że dana grupa wiekowa nie kupowała leków tego typu. Ilość leków została wyrażona w skali logarytmicznej.
|
1 2 |
rozpoznania = pd.read_csv('rozpoznania.csv',sep=';') rozpoznania.head() |
| ID_KONTAKTU | KOD_ROZPOZNANIA | CZY_GLOWNA | |
|---|---|---|---|
| 0 | 86184950 | 42069 | T |
| 1 | 77833278 | 60015 | T |
| 2 | 39973459 | 507306 | T |
| 3 | 96091782 | 7809601 | T |
| 4 | 91312211 | 9401202 | T |
|
1 |
rozpoznania.groupby('CZY_GLOWNA')['CZY_GLOWNA'].count() |
|
1 2 3 4 |
CZY_GLOWNA N 1913513 T 10885114 Name: CZY_GLOWNA, dtype: int64 |
Zazwyczaj udar mózgu był głównym rozpoznaniem choroby.
Panie Łukaszu,
Kwestia prezentacyjna wyników (tabelki, wykresy) w tym artykule jest bardzo słaba. Tabelki rozjeżdżają się poza marginesy (wychodzą na szare tło), wykresy są małe i nie można z nich nic odczytać. Kod sam w sobie też jest mały – nie zastanawiał się Pan nad tym by wielkość czcionki dla kodu była taka sama jak dla normalnego tekstu? Przy przejściu z tekstu na kod trzeba skupić wzrok i oko co chwila się akomoduje – osobiście dla mnie jest to nieprzyjemne.
Czytam Pana artykuły z miłą chęcią, bo oprócz wyciągania ciekawych wniosków, siatka prezentacyjna jest bardzo dobra – ma Pan swój styl. Natomiast ten artykuł jest najgorszy ze wszystkich jakie Pan umieścił – pod względem prezentacji wykresów i tabel. Wykresy w matplotlibie mogą być jeszcze ładniejsze niż w ggplot2 (proszę nad nimi popracować jeszcze i pobawić się większą ilością parametrów graficznych), trzeba się trochę więcej nakodzić, ale efekty są powalające.
M_oże ja, prosty i z prostackim językiem człek powiększyłem obraz i przeczytałem z zrozumieniem.
A_jak se mONdry człeku poćwiczysz oczy na rożnej wielkości czcionki to i mUzg dotlenisz.
T_o sprawi zrozumienie treści.
O_budz się i zacznij jeść zdrowo to nie będziesz leków jadł.
Ł_aknięcie wiedzy sprawi, ze bzdur nie będziesz pisał.
Artykuł świetny. Daje mocno do myślenia. I chodzi o BigFarma, TV, białe kitle.