Ciąg dalszy rozpoznawania pisanych ręcznie liczb. Potraktujemy obrazki jak obrazki (a nie jak wektory).
Dla przypomnienia:
- w zerowej części przygotowaliśmy zbiór danych (aby finalnie korzystać i tak z tego z Kaggle ;) i zobaczyliśmy jak wyglądają przykładowe liczby
- w części pierwszej przygotowaliśmy modele w oparciu o
XGBoost(najlepszy osiągnięty wynik to 87.1% trafności przewidywań) oraz o prostą sieć neuronową (FF, feed-forward) z wykorzystaniem pakietunnet(najlepszy wyniki to 71.7%, ale liczone to było na fragmencie danych) - w części drugiej zainstalowaliśmy bibliotekę
Keraswraz z back-endem w postacitensorflow, poznaliśmy znaczenie współczynników loss, val_loss, acc oraz val_acc oraz przygotowaliśmy kilka modelów, z których najlepszy dał wynik około 97% poprawności rozpoznania liczb. Zrozumieliśmy (mam nadzieję) również logikę stojącą za budowaniem architektury sieci polegającą na składaniu kolejnych warstw jedna za drugą. Zobaczyliśmy również skąd mogą wynikać błędy klasyfikacji (te różne rodzaje czwórek rozpoznane jako dziewiątki na końcu tekstu)
W ostatniej dotychczas części cyklu traktowaliśmy dane o każdej z liczb w zbiorze uczącym jako wektor (czyli ciąg 784 liczb). Dzisiaj każdą liczbę potraktujemy poprawnie – jako obraz.
Zaczniemy od wczytania pakietów oraz danych:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
library(keras) library(tidyverse) # data set from https://www.kaggle.com/c/digit-recognizer/data train_data_path <- "data/train.csv" test_data_path <- "data/test.csv" # wczytanie danych train <- read_csv(train_data_path) y_train <- to_categorical(train$label) x_train <- train[, -1] %>% as.matrix() # rozmiary danych img_rows <- 28 img_cols <- 28 num_classes <- 10 # liczba epochów EPOCHS <- 30 |
Przy okazji wprost wpisaliśmy stałe określające wielkość danych (rozmiar obrazków i liczbę klas) oraz liczbę epochów jaką będziemy trenować nasze modele (dobrze mieć to w stałej, żeby zmieniać w jednym miejscu w kodzie).
Pamiętając naukę z poprzedniej części przeskalujemy dane z zakresu 0-255 do 0-1 – dawało to dużo lepsze wyniki:
|
1 |
x_train <- x_train / 255 |
Dodatkowo w przypadku traktowania przez sieć obrazów jako obrazów (czyli macierzy a nie wektorów) musimy odpowiednio przygotować dane:
|
1 2 3 |
x_train <- array_reshape(x_train, c(nrow(x_train), img_rows, img_cols, 1)) input_shape <- c(img_rows, img_cols, 1) |
Jedynka w powyższych liniach mówi o tym, że mamy jedną warstwę koloru (obrazy w odcieniach szarości). Dla kolorowych obrazów byłaby to trójka: każdy obrazek rozłożony byłby na trzy macierze, po jednej dla każdej składowej koloru (R, G, B). Ciekawym krokiem mogłoby być przekształcenie obrazów RGB do przestrzeni CMYK (używanej w druku).
Powstały twór w matematyce nazywa się tensorem.
Nasza sieć (architektura typu CNN) będzie składać się z kilku rodzajów warstw:
- warstw Conv2D – konwolucyjnej, po polsku splotu (od splotu funkcji)
- warstw MaxPooling – zmieniającej rozdzielczość obrazka (wybieranie na przykład co drugą kolumnę i co drugi wiersz z macierzy)
- warstw Dense – czyli w pełni połączonych ze sobą neuronów
- warstw Dropout przepuszczających tylko fragment danych (aby zapobiec przeuczeniu sieci)
- warstwy Flatten spłaszczającej macierze do wektorów (bo na końcu musimy dostać prawdopodobieństwo przynależności liczby z obrazka do jednej z dziesięciu klas 0-9)
Trzy ostatnie typy warstw są w miarę zrozumiałe (mam nadzieję) ale co robi warstwa konwolucyjna (Conv2D)? Najprościej mówiąc stosuje filtr na obrazku. Filtry są macierzą kwadratową (mogą mieć różną wielkość – najczęściej 3×3, 5×5, czasem 7×7), a ich działanie polega w dużym uproszczeniu na pomnożeniu kwadratowego wycinka obrazka przez macierz opisującą filtr. Z mnożenia macierzy przez siebie dostajemy jedną liczbę, którą zapisujemy w tym samym punkcie co środek wycinka.
Czyli dla kolejnych wierszy (Y) i kolumn (X) obrazka pobieramy na przykład 4 punkty:
- (X, Y)
- (X + 1, Y)
- (X, Y + 1)
- (X + 1, Y + 1)
i mnożymy przez macierz definiującą filtr (w tym przypadku macierz 2×2). Bardzo fajne, interaktywne (można wybrać różne filtry) zobrazowanie tego mechanizmu znajdziecie na tej stronie – tam przykłady oparte są na macierzy 3×3. W Photoshopie też istnieje odpowiednie do tego celu narzędzie.
Drugi krok w naszej sieci to warstwa Max Pooling. Operacja jest podobna do zastosowania filtru, z tym że tutaj nie mamy mnożenia przez macierz filtru, a wyciągamy największą wartość z wycinka obrazka. Różnica dodatkowa – okno przesuwa się o swoją szerokość (w Conv2D przesuwamy okno o jeden punkt). Dzięki temu uzyskujemy obraz odpowiednio mniejszy – to wpływa na rozmiar danych w sieci i tym samym liczbę cech, które sieć musi wytrenować.
Co to wszystko daje? Warstwa konwolucyjna pozwala na znalezienie cech obrazu (na przykład krawędzie przy zastosowaniu filtrów typu emboss). Zobaczmy na przykładzie (przygotowanym w Excelu):
Na początek weźmy coś co wygląda jak dwójka:

Widzimy, że dla (dość losowego filtru) wyższe wartości mnożenia obrazu przez filtr uzyskały miejsca zaokrągleń – prawy górny i lewy dolny róg liczby. Czerwonymi kółkami zaznaczyłem te miejsca na wyniku finalnym (obrazek -> conv 2d -> max pooling 3×3).
Co osiągniemy dla innej liczby?

Dziewiątka jest dość podobna, też ma zaokrąglenie w prawym górnym rogu. Można więc spodziewać się, że liczby z takim zaokrągleniem będą podobne do 2, 9 (i pewnie 8, może też 7). Sprawdźmy jeszcze jedynkę:

Ta konkretna jedynka również wskazuje na cechę “zaokrąglony prawy górny róg”. Ale nie ma niczego w lewej dolnej części i ma też inny układ środka (tu gdzie jest nóżka).
Tylko jedna operacja i tym samym jedna wykryta cecha, a już w małym stopniu potrafimy rozpoznać kilka liczb (odrzucając inne).
Architektura naszej sieci buduje kilkadziesiąt warstw Conv2D tym samym rozpoznanych zostanie kilkadziesiąt cech. Co więcej – stosujemy dwie warstwy Conv2D po sobie, więc wynik jest jeszcze bardziej zakręcony (cechy są wzmocnione). Po zmniejszeniu ilości danych (przez max pooling) znowu robimy podwójny Conv2D i znowu MaxPooling – w efekcie z obrazu 28×28 punktów pozostaje nam tablica 7×7 (pierwszy max pooling zmniejsza liczbę punktów o połowę, drugi o kolejną). To już można trenować w rozsądnym czasie. Na zakończenie nasz model spłaszcza dane z obrazu do wektora i dalsze obliczenia przebiegają już standardowo w ramach warstwy dense.
W obu przypadkach (Conv2D i MaxPooling) problemem są brzegi obrazu (co zrobić z punktami, których nie ma?) – można dodawać pasy zero o odpowiedniej szerokości, można brać wewnętrzną część obrazu (tak, żeby okno mieściło się w całości w ramach obrazka), można powielać brzegowe wiersze/kolumny. Rozwiązań jest kilka, każde z nich może wpłynąć na wyniki obliczeń.
Nie udało mi się wydobyć wprost z modelu wyglądu kolejnych warstw – może ktoś ma na to sposób?
Model 1
Zbudujmy pierwszy model będący kombinacją omówionych warstw.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
model <- keras_model_sequential() %>% # architektura sieci: # splot - 32 filtry 3x3 layer_conv_2d(filters = 32, kernel_size = c(3,3), activation = 'relu', input_shape = input_shape) %>% # splot - 64 filtry 3x3 layer_conv_2d(filters = 64, kernel_size = c(3,3), activation = 'relu') %>% # max pooling 2x2 layer_max_pooling_2d(pool_size = c(2, 2)) %>% # 25% przechodzi layer_dropout(rate = 0.25) %>% # splaszczenie do wektora layer_flatten() %>% # warstwa normalna - kazdy z kazdym layer_dense(units = 128, activation = 'relu') %>% # 50% przechodzi layer_dropout(rate = 0.5) %>% # odpowiedz - prawdopodobienstwo dla kazdej klasy layer_dense(units = num_classes, activation = 'softmax') %>% # kompilacja modelu: compile( loss = loss_categorical_crossentropy, optimizer = optimizer_adadelta(), metrics = c('accuracy') ) summary(model) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
## ___________________________________________________________________________ ## Layer (type) Output Shape Param # ## =========================================================================== ## conv2d_1 (Conv2D) (None, 26, 26, 32) 320 ## ___________________________________________________________________________ ## conv2d_2 (Conv2D) (None, 24, 24, 64) 18496 ## ___________________________________________________________________________ ## max_pooling2d_1 (MaxPooling2D) (None, 12, 12, 64) 0 ## ___________________________________________________________________________ ## dropout_1 (Dropout) (None, 12, 12, 64) 0 ## ___________________________________________________________________________ ## flatten_1 (Flatten) (None, 9216) 0 ## ___________________________________________________________________________ ## dense_1 (Dense) (None, 128) 1179776 ## ___________________________________________________________________________ ## dropout_2 (Dropout) (None, 128) 0 ## ___________________________________________________________________________ ## dense_2 (Dense) (None, 10) 1290 ## =========================================================================== ## Total params: 1,199,882 ## Trainable params: 1,199,882 ## Non-trainable params: 0 ## ___________________________________________________________________________ |
Widzimy, że do rozpoznania (wyliczenia) jest prawie 1.2 mln wag. Sporo. Sporo też to trwa.
Ważny element, o którym nie wspomniałem to ReLU czyli funkcja aktywacji zmieniająca obliczone wagi. Opcji jest kilka – doczytajcie proszę w materiałach w sieci. Funkcja ReLU działa tak, że dla wartości ujemnych zwraca 0, a dla dodatnich – po prostu argument funkcji. Ma to sens w tym przypadku – na koniec mamy dostać prawdopodobieństwo, a ono nie może być ujemne.
Wytrenujmy więc nasz model:
|
1 2 3 4 5 6 7 8 9 10 11 |
history <- model %>% fit( x_train, y_train, batch_size = 128, epochs = EPOCHS, verbose = 1, validation_split = 0.2 ) plot(history) |
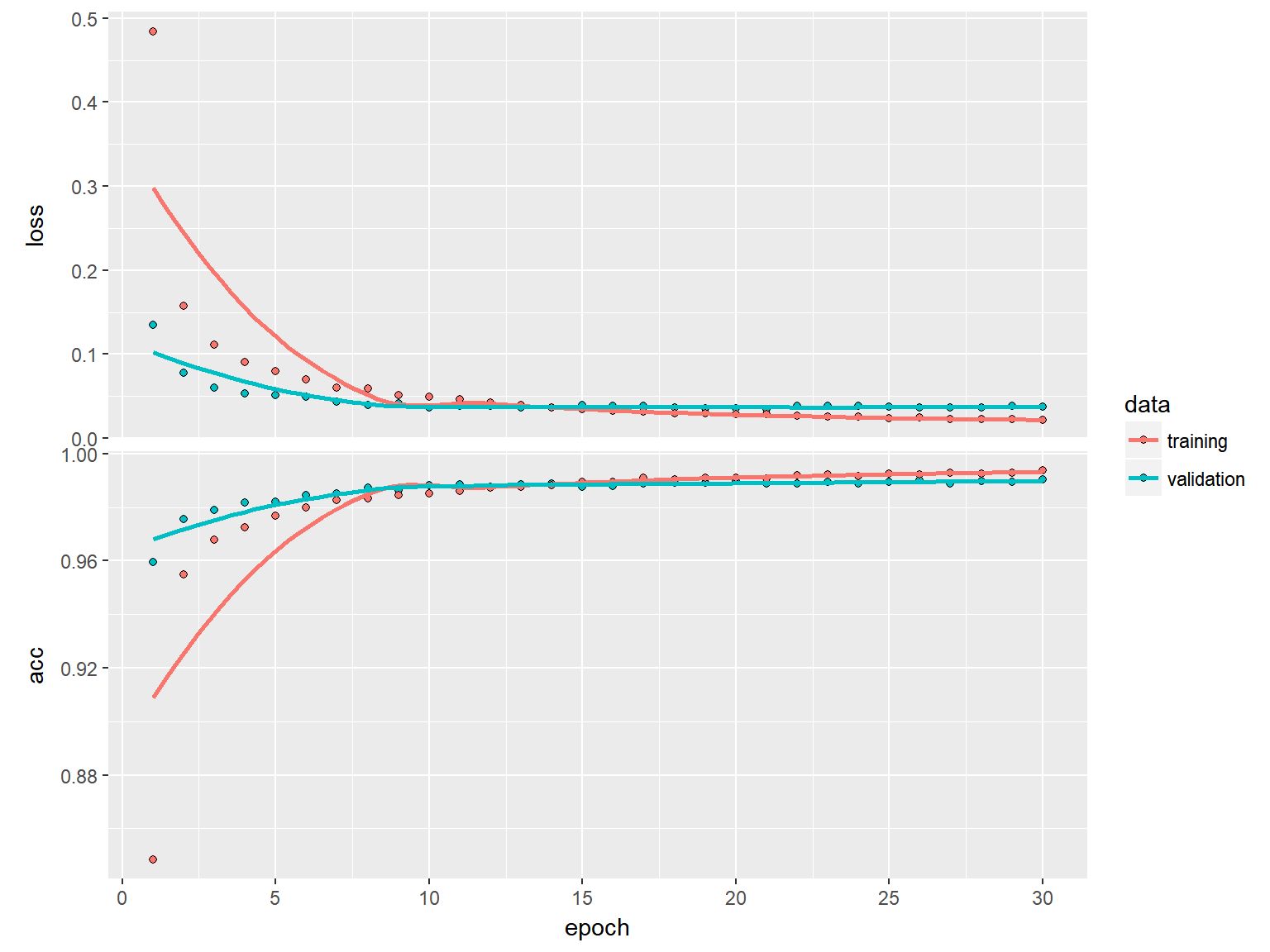
Wynik to dokładność rozpoznawania liczb na poziomie 99.04%. Dla przypomnienia XGBoost dał wartość około 87%, prosta sieć oparta na trzech warstwach dense (model Model 4b z poprzedniej części) dał 96.9%. Mamy zatem rekord i tym samym najlepszy dotychczasowy model.
Czy 2 punkty procentowe to duży zysk? To może być dyskusyjne – niby mało, ale w okolicach 99% jest już ciasno i każdy urwany 0.1% może być sukcesem. 2% zbioru treningowego (42 tysiące) to 840 liczb. Jeśli byłyby to na przykład osoby wskazane do przeprowadzenia jakichś bardzo drogich badań to 840 dodatkowych badań może sporo kosztować. Ale z drugiej strony jeśli miałby to być oszczędność polegająca na tym, że nie trzeba czytać 840 stron tekstu to już sukces, prawda? Wkraczamy na pole z zagadnieniami filozoficznymi: lepiej zbudować model z lepszymi wynikami czy pozwolić sobie na jakiś stopień błędu?
Ważny jest też czas. Na moim domowym komputerze (jakiś pewnie 7 letni Vaio z procesorem i3) trenowanie modelu trwało około 4 godzin i 20 minut. Przy 15 epochach osiągnięty val_acc to około 99% – po wykresie widać, że więcej niż 15 rund nie przynosi poprawy wyniku (więc można było skończyć po 2 godzinach :)
Model 2
Model ten zaczerpnięty jest bezpośrednio z kernela z Kaggle, który uzyskał jeden z lepszych wyników w konkursie. Polecam zapoznanie się w oryginałem, a przy okazji możecie sami zobaczyć jak łatwo przenieść architekturę sieci z Pythona na R:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
model <- keras_model_sequential() %>% # architektura sieci: # splot layer_conv_2d(filters = 32, kernel_size = c(5,5), activation = 'relu', padding = 'same', input_shape = input_shape) %>% # splot layer_conv_2d(filters = 32, kernel_size = c(5,5), activation = 'relu', padding = 'same') %>% # max pooling dla macierzy 2x2 layer_max_pooling_2d(pool_size = c(2, 2)) %>% # 25% przechodzi layer_dropout(rate = 0.25) %>% # splot layer_conv_2d(filters = 64, kernel_size = c(3,3), activation = 'relu', padding = 'same', input_shape = input_shape) %>% # splot layer_conv_2d(filters = 64, kernel_size = c(3,3), activation = 'relu', padding = 'same') %>% # max pooling dla macierzy 2x2 layer_max_pooling_2d(pool_size = c(2, 2), strides = c(2,2)) %>% # 25% przechodzi layer_dropout(rate = 0.25) %>% # splaszczenie do wektora layer_flatten() %>% # warstwa normalna - kazdy z kazdym layer_dense(units = 256, activation = 'relu') %>% # 50% przechodzi layer_dropout(rate = 0.5) %>% # odpowiedz - prawdopodobienstwo dla kazdej klasy layer_dense(units = num_classes, activation = 'softmax') %>% # kompilacja modelu: compile( loss = loss_categorical_crossentropy, optimizer = optimizer_rmsprop(lr=0.001, rho=0.9, epsilon=1e-08, decay=0.0), metrics = c('accuracy') ) summary(model) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
## ___________________________________________________________________________ ## Layer (type) Output Shape Param # ## =========================================================================== ## conv2d_3 (Conv2D) (None, 28, 28, 32) 832 ## ___________________________________________________________________________ ## conv2d_4 (Conv2D) (None, 28, 28, 32) 25632 ## ___________________________________________________________________________ ## max_pooling2d_2 (MaxPooling2D) (None, 14, 14, 32) 0 ## ___________________________________________________________________________ ## dropout_3 (Dropout) (None, 14, 14, 32) 0 ## ___________________________________________________________________________ ## conv2d_5 (Conv2D) (None, 14, 14, 64) 18496 ## ___________________________________________________________________________ ## conv2d_6 (Conv2D) (None, 14, 14, 64) 36928 ## ___________________________________________________________________________ ## max_pooling2d_3 (MaxPooling2D) (None, 7, 7, 64) 0 ## ___________________________________________________________________________ ## dropout_4 (Dropout) (None, 7, 7, 64) 0 ## ___________________________________________________________________________ ## flatten_2 (Flatten) (None, 3136) 0 ## ___________________________________________________________________________ ## dense_3 (Dense) (None, 256) 803072 ## ___________________________________________________________________________ ## dropout_5 (Dropout) (None, 256) 0 ## ___________________________________________________________________________ ## dense_4 (Dense) (None, 10) 2570 ## =========================================================================== ## Total params: 887,530 ## Trainable params: 887,530 ## Non-trainable params: 0 ## ___________________________________________________________________________ |
Ciekawostka – sieć bardziej rozbudowana (więcej warstw), a mniej parametrów treningowych (wag). Co nie znaczy, że szybciej się to policzy… Niech się liczy:
|
1 2 3 4 5 6 7 8 9 10 11 |
history <- model %>% fit( x_train, y_train, batch_size = 128, epochs = EPOCHS, verbose = 1, validation_split = 0.2 ) plot(history) |
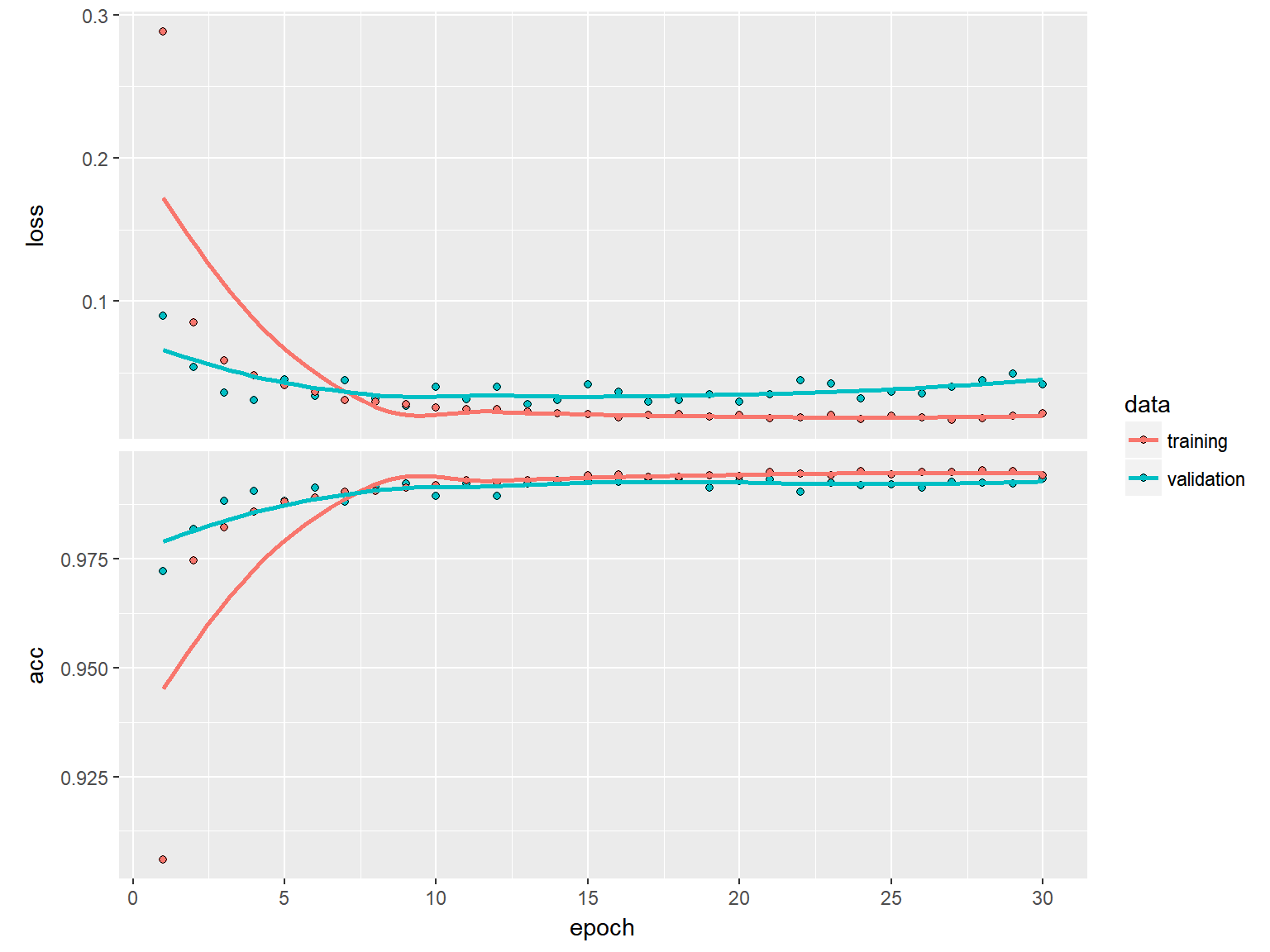
Wynik 99.35% osiągnięty w czasie prawie 12 godzin. Trzeba chyba zainwestować w jakiś serwer wirtualny z GPU (taki p2.8xlarge z AWSu wydaje się optymalny do zabawy na godziny)… Dobrym pomysłem jest też wykorzystanie Kaggle do testów: budujemy sobie kernel i odpalamy. Problem tylko jest taki, że skrypt musi wykonać się w godzinę.
Jak wykorzystać model do predykcji na nowych danych? Dokładnie tak samo jak w poprzedniej części:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# wczytujemy dane testowe test <- read_csv(test_data_path) # przekształcamy je odpowiednio - analogicznie do danych treningowych x_test <- test %>% as.matrix() x_test <- x_test / 255 x_test <- array_reshape(x_test, c(nrow(x_test), img_rows, img_cols, 1)) # predykcja pred_probs <- predict_proba(model, x_test, batch_size = 32, verbose = 1) pred_class <- predict_classes(model, x_test, batch_size = 32, verbose = 1) |
Na tym kończymy cykl związany z rozpoznawaniem liczb pisanych ręcznie. Można (według tego co napisano w kernelach na Kaggle w konkursie z którego wzięliśmy dane) zastosować jeszcze kilka sztuczek z których za najciekawszą uważam przekształcanie danych treningowych (delikatne przesuwanie obrazków, obracanie czy skalowanie). Warto też przejrzeć artukuły ze strony z oryginalnymi danymi.
Dodatkowo polecam inne opracowania (trochę więcej matematyki tam znajdziecie i przede wszystkim obrazki, które ułatwiają zrozumienie tego, co starałem się ubrać w słowa) tego samego tematu:
- analogiczny do mojego cykl u Krzysztofa Sopyły – w Pythonie
- rozpoznawanie statków na zdjęciach satelitarnych na blogu firmy Appsilon – w R
Identycznie można zbudować sieć do rozpoznawania kotów i psów na zdjęciach. Spróbujcie poszukać odpowiedniego datasetu, na przykład na Kaggle (jak zwykle ;) i zastosować powyższe modele.
Koniec zabawy z danymi ze zbioru MNIST to nie koniec o sieciach neuronowych. Będzie jeszcze coś, czekajcie na więcej i poszerzajcie wiedzę samodzielnie. Pamiętając o fanpage Dane i analizy :)
Fajne. Choć dla uczciwości należałoby sprawdzić jak xgboost zachowa się na tych uproszczonych/przeskalowanych danych wejściowych.