W którym miejscu można skrócić proces, na której fazie trwa on najdłużej?
Dzisiaj zajmiemy się analizą dowolnego procesu, w którym można wskazać jakieś fazy. Zadanie wzięło się z pracy, którą wykonuję na co dzień: który element procesu wytwórczego oprogramowania trwa najdłużej? Czy to, że przygotowanie systemu IT trwa tak długo to wina IT (analiza wymagań, przygotowanie dokumentacji dla programistów, samo programowanie, testy) czy biznesu (przygotowanie wymagań biznesowych, oceny opłacalności rozwiązania, przygotowanie dokumentacji do decyzji wszelakich komitetów sterujących)? Czy jak zamówię przesyłkę dzisiaj to dotrze ona do mnie w krótszym czasie niż przy zamówieniu za miesiąc? Ile czasu będę czekał na pizzę? Dlaczego klient w sklepie (urzędzie, banku, placówce służby zdrowia) obsługiwany jest tak długo? Dlaczego w przychodni zapisuje się na wizyty co 15 minut, jak i tak są opóźnienia?
Weźmy przykład teoretyczny, chociaż dość realny – zakupy przez internet. Możemy wyróżnić kilka podstawowych faz:
- zamówienie towaru – tutaj to klient jest odpowiedzialny za proces wyboru towaru, dodanie do koszyka i opłacenie zamówienia. Nasz proces zaczyna się w momencie kliknięcia “Kupuję”
- po weryfikacji zamówienia sklep oczekuje na płatność
- po otrzymaniu płatności – przystępuje do realizacji zamówienia, czyli procesie polegającym kolejno na:
- zebraniu towaru z magazynu
- zapakowaniu towaru – przygotowanie paczki do przesłania
- nadaniu paczki do transportu
- tutaj sklep właściwie kończy swoją działalność, a pałeczkę (paczkę) przejmuje dostawca:
- kurier odbiera paczkę ze sklepu (albo sklep nadaje ją na poczcie)
- firma kurierska (lub poczta) przewozi paczkę do odbiorcy
- kurier przekazuje paczkę klientowi sklepu
- kurier zaznacza w jakimś systemie, że paczka została dostarczona
- sklep otrzymuje informację, że zamówienie zostało zrealizowane
Do analizy takiego procesu wystarczą nam informacje o momentach (datach) na przykład zakończenia każdej z faz. A później wystarczą zainstalowane w R pakiety:
|
1 2 3 4 |
library(tidyverse) # obróbka danych i wykresy library(lubridate) # operacje na datach library(forcats) # porządkowanie kolejności factorów przy wykresach library(readxl) # do wczytania arkusza Excela |
Skąd wziąć dane o procesie? Można poszukać w sieci, można wziąć z jakiegoś sklepu, można na przykład próbować scrapować strony typu śledzenie przesyłek poszczególnych kurierów (zgadywać numer przesyłki i sprawdzać jej historię).
Można też je wygenerować – ja dane przykładowe przygotowałem w Excelu. W czterech kolejnych kolumnach wpisałem:
- numer zamówienia
- datę zamówienia, która oznacza moment zakończenia procesu składania zamówienia na towar
- datę zakończenia procesu pakowania przesyłki
- datę zakończenia procesu wysyłki
- datę doręczenia przesyłki do adresata
Numer zamówienia to po prostu kolejny numer (nie ma on żadnego znaczenia, ważne żeby był unikalny).
Datę zamówienia wygenerowałem losowo – od aktualnej daty odjąłem losową liczbę. Przedział z którego losujemy wybrałem tak, aby najwcześniejsza data była jeszcze w 2017 roku. Odpowiednia formuła to =DZIŚ()+LOS.ZAKR(-330;-20).
Datę pakowania przygotowałem dodając do daty zamówienia losową liczbę zależną od miesiąca daty złożenia zamówienia. Tylko po to, aby uzyskać różne wyniki dla różnych miesięcy (zasymulować sezonowość).
Data wysyłki to z kolei data pakowania plus kilka (losowa wartość, także zależna od miesiąca) dni.
Datę doręczenia przygotowałem analogicznie. Ważne: liczby dodawane do kolejnych dat (zamówienia, pakowania i wysyłki) losowane są z różnych zakresów, tak aby uzyskać różne średnie długości faz.
Ten sam proces można oczywiście przygotować w R.
Potrzebujemy (głównie dla wygody) jeszcze słownika statusów i ich kolejność w drodze przez proces:
|
1 2 3 |
statusy <- c("zamowienie", "pakowanie", "wysylka", "dostawa") kolejnosc <- tibble(p = statusy[1:(length(statusy)-1)], k = statusy[2:length(statusy)]) |
Przygotowane dane wczytujemy i nieco przekształcamy:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# wczytanie danych z excela zamowienia <- read_excel("Dane_symulowane.xlsx") # wybor i nazwanie potrzebnych kolumn zamowienia <- zamowienia[, c(2, 6, 7, 8, 9)] colnames(zamowienia) <- c("NrZamowienia", "zamowienie", "pakowanie", "wysylka", "dostawa") # lista długa zamiast szerokiej zamowienia <- zamowienia %>% gather(Status, Data, zamowienie, pakowanie, wysylka, dostawa) %>% mutate(Data = as.Date(Data)) %>% mutate(Status = fct_relevel(Status, statusy)) |
Lista w postaci długiej odpowiada temu co może przyjść z jakiegoś systemu:
|
1 |
head(zamowienia %>% arrange(NrZamowienia, Data), 10) |
| Nr zamówienia | Status | Data |
|---|---|---|
| ZAM_0001 | zamowienie | 2017-03-23 |
| ZAM_0001 | pakowanie | 2017-03-30 |
| ZAM_0001 | wysylka | 2017-04-04 |
| ZAM_0001 | dostawa | 2017-04-24 |
| ZAM_0002 | zamowienie | 2017-03-14 |
| ZAM_0002 | pakowanie | 2017-03-21 |
| ZAM_0002 | wysylka | 2017-03-25 |
| ZAM_0002 | dostawa | 2017-04-20 |
| ZAM_0003 | zamowienie | 2017-07-06 |
| ZAM_0003 | pakowanie | 2017-07-19 |
Widać, że każde zamówienie przechodzi przez kolejne fazy kończące się w określonym momencie (tutaj wystarczy dokładność co do dnia – przy zamówieniu pizzy liczą się minuty).
Zobaczmy teraz przykładowe zamówienia na osi czasu:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
zamowienia %>% # losujemy 15 numerów zamówień filter(NrZamowienia %in% sample(unique(as.character(zamowienia$NrZamowienia)), 15)) %>% # z tabeli długiej robimy szeroką spread(Status, Data) %>% # to tylko dla porządku na wykresie - żeby numery zamówień były wg kolejności na osi mutate(NrZamowienia = fct_rev(NrZamowienia)) %>% # rysujemy wykresik ggplot() + # długość fazy zamówienia, czyli weryfikacja zamówienia i zerbranie towaru z magazynu geom_segment(aes(x = zamowienie, xend = pakowanie, y = NrZamowienia, yend = NrZamowienia), color = "grey20", size = 3) + # długość fazy pakowania, czyli przygotowania do wysyłki geom_segment(aes(x = pakowanie, xend = wysylka, y = NrZamowienia, yend = NrZamowienia), color = "grey50", size = 3) + # długość fazy transportu do klienta, czyli do momentu doręczenia paczki geom_segment(aes(x = wysylka, xend = dostawa, y = NrZamowienia, yend = NrZamowienia), color = "grey80", size = 3) + # dodajemy jeszcze punkty początku i końca procesu geom_point(aes(zamowienie, NrZamowienia), color = "red", size = 4) + geom_point(aes(dostawa, NrZamowienia), color = "red", size = 4) + # skalowanie osi i pozostała kosmetyka scale_x_date(date_breaks = "1 month", date_labels = "%B") + labs(title = "Historia przykładowych zamówień", x = "", y = "") |
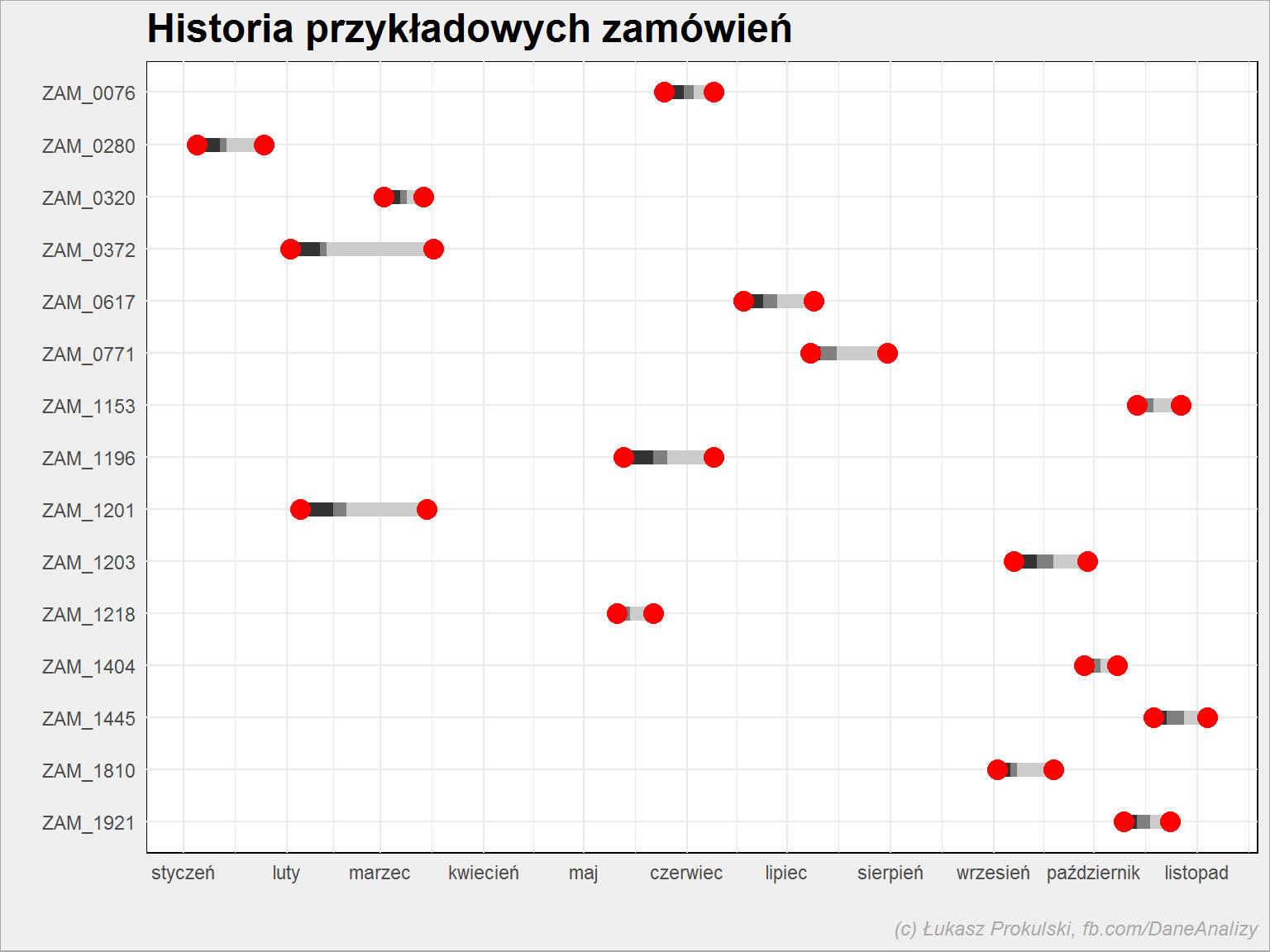
Jak widać różne są długości całego procesu, nie do końca widać jakąś zależność między długością poszczególnych faz (no, najdłuższa jest ostatnia). Tym bardziej chyba nie widać zależności czasu trwania określonej fazy od miesiąca. A przecież w grudniu przed świętami zamówień może być więcej, przesyłek również – wszystko to ma wpływ na długość procesu. Naszym zadaniem jest znaleźć miejsca opóźnień. Miejsca, bo powody to nieco inna analiza.
Na początek sprawdźmy czy w naszych laboratoryjnych danych widać różnice w liczbie trwających faz w ujęciu miesięcznym.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
zamowienia %>% # tylko fazy zakończone do dzisiaj filter(Data < today()) %>% # wszystkie daty ściągamy do 1 dnia miesiąca mutate(Data = make_date(year(Data), month(Data), 1)) %>% # ile elementów w fazie w miesiącu? count(Status, Data) %>% ungroup() %>% # dla porządku na osi mutate(Status = fct_rev(Status)) %>% # wykres ggplot() + geom_tile(aes(Data, Status, fill=n), color = "gray50") + scale_fill_distiller(palette = "RdYlGn") + scale_x_date(date_breaks = "1 month", date_labels = "%B") + theme(legend.position = "bottom") + labs(x = "", y ="", fill = "Liczba zamówień w fazie") |
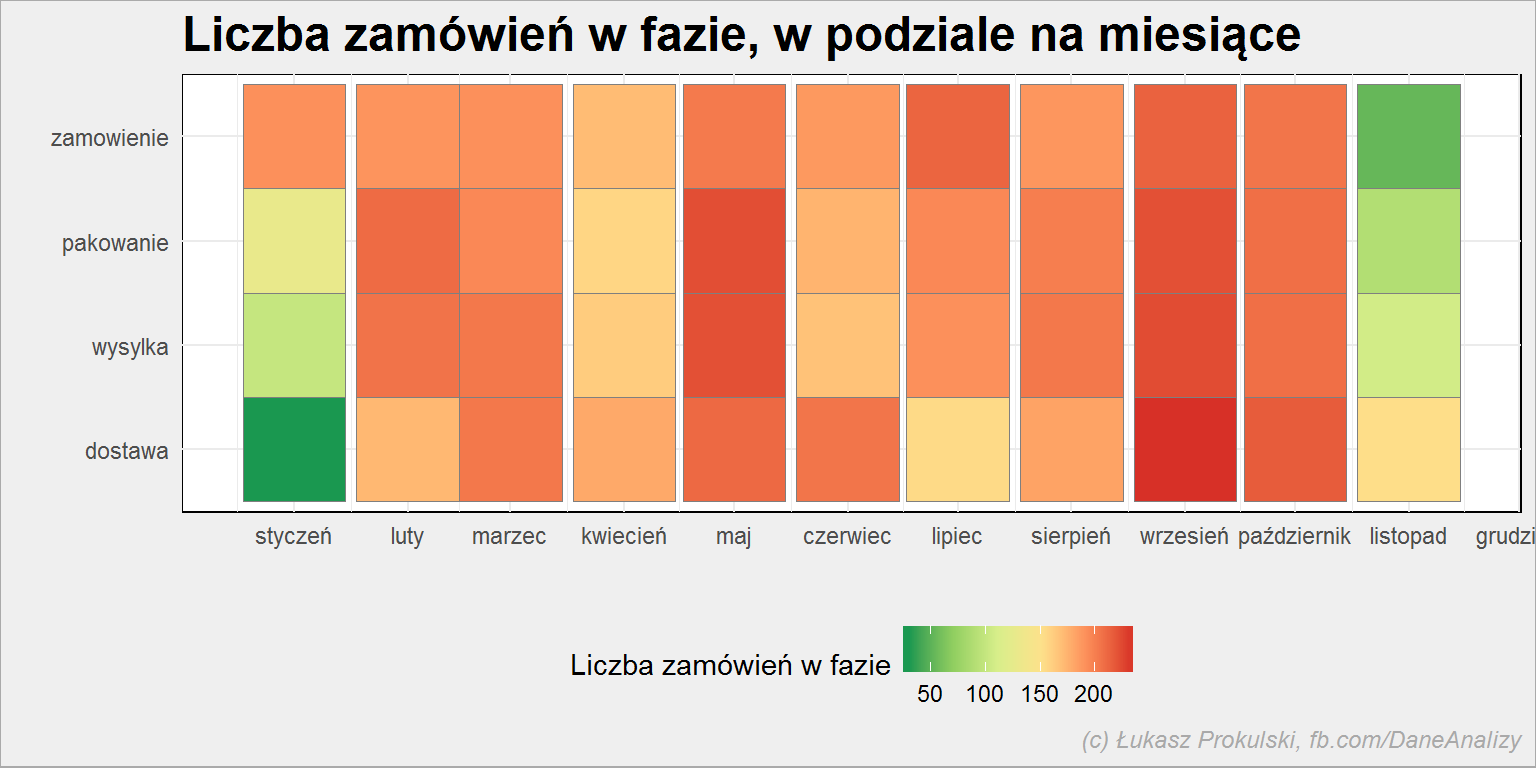
Cały proces jest swego rodzaju kolejką: nie będzie jednej fazy, o ile nie zakończy się poprzednia. Stąd widoczne powyżej w styczniu mniejsze ilości elementów będących w fazach wysyłka, pakowanie czy (to najbardziej) dostawa naszego procesu. Daty i długości faz są dobrane tak, żeby było to wyraźnie widać. Dodatkowo nie mamy historii sprzed 2017 roku. I tak w dostawie w styczniu jest mało towarów, bo nie zdążyły przejść przez zamówienie, wysyłkę i pakowanie.
Takie spojrzenie niewiele nam daje szczerze mówiąc. Policzymy długości każdej z faz dla każdego z zamówień:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
fazy <- zamowienia %>% # potrzbujemy najpierw kolejności faz - dla "aktualnej" fazy dodajemy jej "następnika" left_join(kolejnosc, by = c("Status" = "p")) %>% # teraz łączymy tabelę samą ze sobą - tak, aby uzyskać informację kiedy kończy się następna faza left_join(zamowienia, by = c("NrZamowienia" = "NrZamowienia", "k" = "Status")) %>% # pozostawiamy tylko poprawne dane filter(!is.na(k)) %>% # i nieco je porządkujemy select(NrZamowienia, Faza = k, DataPocz = Data.x, DataKon = Data.y) %>% mutate(CzasTrwania = as.numeric(DataKon - DataPocz)) %>% mutate(Faza = fct_relevel(Faza, statusy)) |
Otrzymamy tabelkę podobną do danych źródłowych, ale już z czasami trwania poszczególnych faz procesu dla każdego z zamówień:
|
1 |
head(fazy %>% arrange(NrZamowienia, DataPocz), 10) |
| Nr zamówienia | Faza | Data początkowa | Data końcowa | Czas trwania fazy |
|---|---|---|---|---|
| ZAM_0001 | pakowanie | 2017-03-23 | 2017-03-30 | 7 |
| ZAM_0001 | wysylka | 2017-03-30 | 2017-04-04 | 5 |
| ZAM_0001 | dostawa | 2017-04-04 | 2017-04-24 | 20 |
| ZAM_0002 | pakowanie | 2017-03-14 | 2017-03-21 | 7 |
| ZAM_0002 | wysylka | 2017-03-21 | 2017-03-25 | 4 |
| ZAM_0002 | dostawa | 2017-03-25 | 2017-04-20 | 26 |
| ZAM_0003 | pakowanie | 2017-07-06 | 2017-07-19 | 13 |
| ZAM_0003 | wysylka | 2017-07-19 | 2017-07-26 | 7 |
| ZAM_0003 | dostawa | 2017-07-26 | 2017-08-22 | 27 |
| ZAM_0004 | pakowanie | 2017-10-10 | 2017-10-16 | 6 |
Zwróćcie uwagę, że brakuje fazy zamówienie. W tym przypadku to oczywiste – zamówienie do data rozpoczęcia procesu, ta faza nie trwa, to wręcz nie jest faza.
Teraz możemy już sprawdzić najważniejsze liczby opisujące rozkład czasów trwania naszych faz: wartości minimalną i maksymalną, średnią i medianę oraz kwartyle i odchylenie standardowe:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
fazy_stat <- fazy %>% group_by(Faza) %>% summarise(Min = min(CzasTrwania), Kwartyl25p = quantile(CzasTrwania, 0.25), Srednia = mean(CzasTrwania), Mediana = median(CzasTrwania), Kwartyl75p = quantile(CzasTrwania, 0.75), Max = max(CzasTrwania), StdDev = sd(CzasTrwania)) %>% ungroup() fazy_stat |
| Faza | Min | Kwartyl 25% | Średnia | Mediana | Kwartyl 75% | Max | Odchylenie standardowe |
|---|---|---|---|---|---|---|---|
| pakowanie | 2 | 5 | 7.3870 | 7 | 9 | 28 | 3.710137 |
| wysylka | 1 | 2 | 4.2185 | 4 | 6 | 15 | 2.453318 |
| dostawa | 2 | 8 | 15.1625 | 13 | 20 | 57 | 9.452501 |
Swoją drogą podobny efekt można uzyskać w zdecydowanie krótszym kodzie (interesuje nas część CzasTrwania) – sami sprawdźcie co da:
|
1 2 3 |
fazy %>% split(.$Faza) %>% map(summary) |
Wprawne oko wyłowi z liczb wszystkie interesujące informacje, ale dla zarządu potrzebny jest slajd, zatem wykres:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
# potrzebne do skalowania wykresu max_czas_fazy <- max(fazy_stat$Max) fazy %>% filter(DataKon < today()) %>% mutate(Faza = fct_rev(Faza)) %>% ggplot() + geom_boxplot(aes(Faza, CzasTrwania, fill = Faza), show.legend = FALSE) + coord_flip() + scale_y_continuous(limits = c(0, max_czas_fazy), breaks = pretty(1:max_czas_fazy, 10)) + labs(title = "Rozkład długości faz", x ="", y = "Czas trwania fazy") |
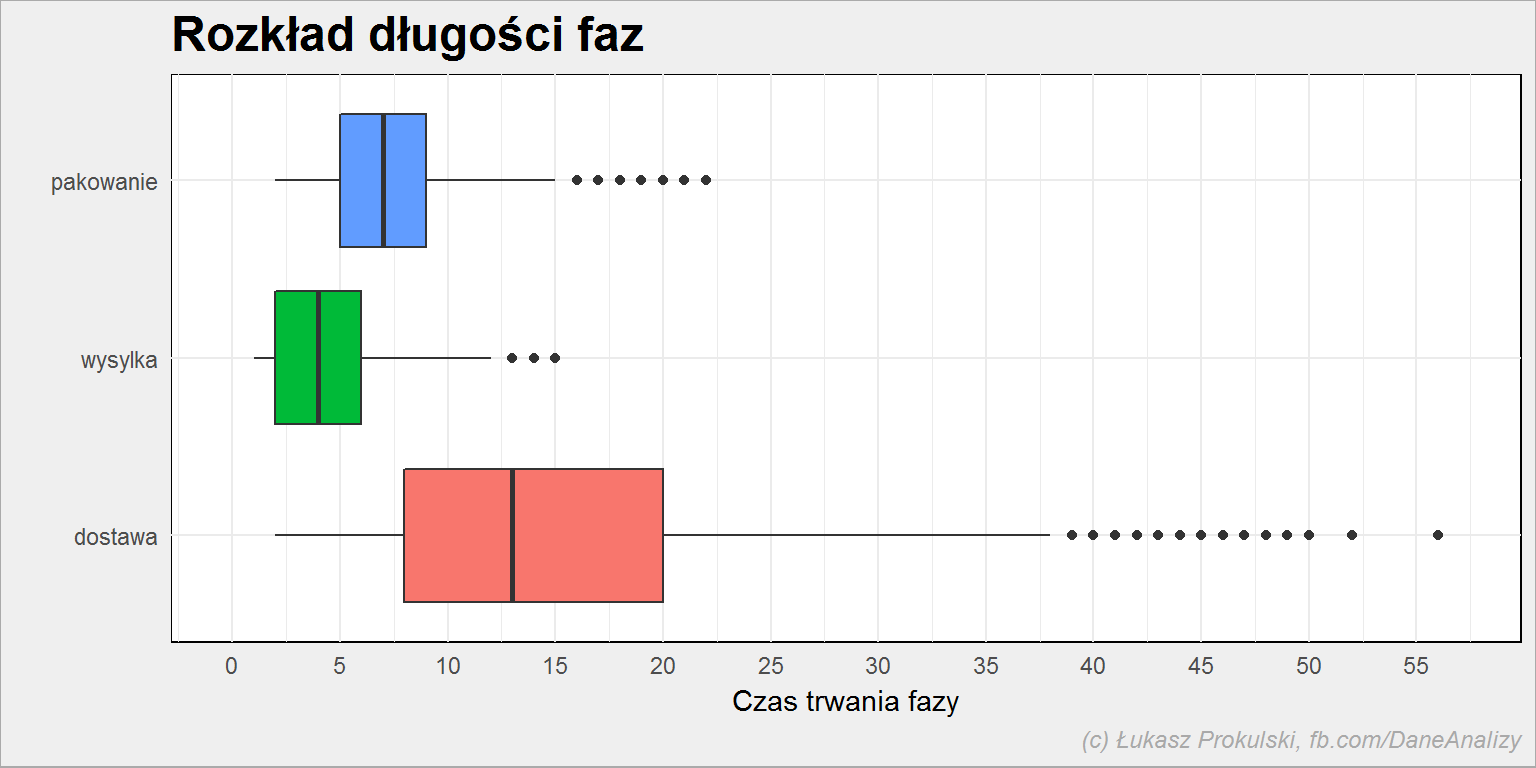
Co my tutaj mamy?
- Pakowanie zajmuje średnio 7 dni (7 to mediana, średnia to 7.4)
- wysyłka jest najkrótsza, ale zajmuje (mediana) 4 dni
- najdłuższa jest dostawa – mediana to 13 dni
Jeśli więc mielibyśmy szukać oszczędności na czasie to pierwszym punktem powinna być weryfikacja firmy dostarczającej przesyłki.
Warto też zastanowić się w szczegółach nad pakowaniem – czy tyle trwa zebranie towaru z magazynu? Za może samo przygotowanie paczki? Dokładna analiza powinna obejmować też sprawdzenie jak to wygląda dla poszczególnych zamówień (jakich kategorii towarów, wielkości towaru, może położenia magazynu, kto wtedy był na zmianie). W każdym razie podstawowa statystyka to dobry punkt zaczepienia.
Kolejnym krokiem jaki można wykonać to sprawdzenie czy długość faz zależy w jakiś sposób od czasu realizacji zamówienia (pamiętacie wspomniane święta? Co roku poczta i kurierzy mają więcej paczek, zatem dostarczają dłużej, bo sortownie nie wyrabiają).
|
1 2 3 4 5 6 7 8 9 10 11 |
fazy %>% filter(DataKon < today()) %>% group_by(DataPocz, Faza) %>% summarise(mCZ = mean(CzasTrwania)) %>% ungroup() %>% ggplot() + geom_smooth(aes(DataPocz, mCZ, group = Faza, color = Faza), show.legend = FALSE) + facet_wrap(~Faza, ncol = 1, scales = "free_y") + scale_x_date(date_breaks = "1 month", date_labels = "%B") + labs(title = "Średnie długości faz w zależności od miesiąca", x = "", y = "Długość fazy", fill = "") |
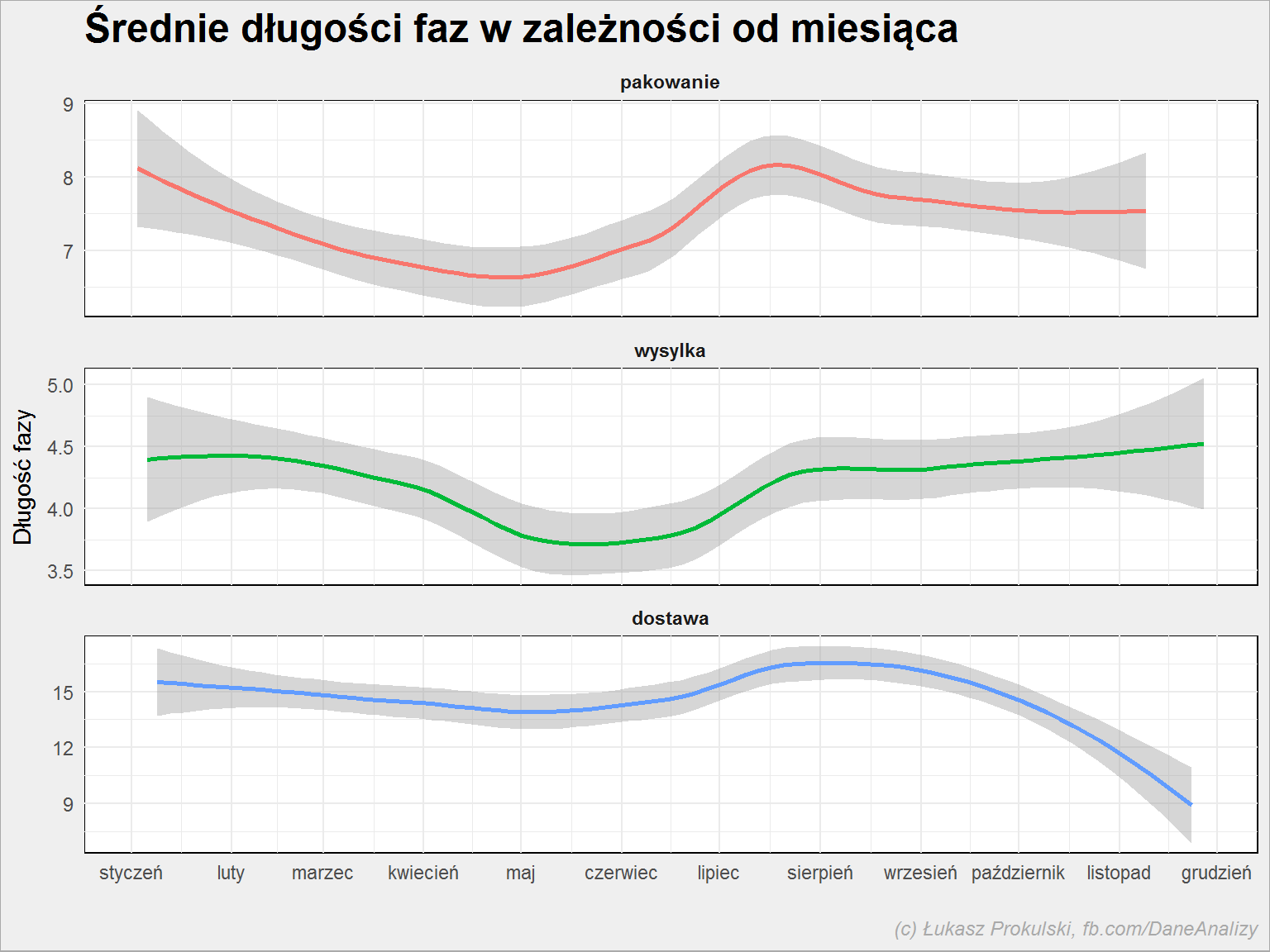
Oczywiście dane spreparowałem w taki sposób aby było widać ten efekt. Powyżej widać średnią (może być równie dobrze mediana) dla poszczególnych faz rozpoczynających się w danym dniu, co ma sens przy dużej liczbie zamówień. Możemy podzielić dane innym kluczem: kolejnym tygodniem roku, dniem tygodnia i tak dalej. Wszystko zależy od charakteru naszego procesu i wpływu kalendarza na jego przebieg.
Przedstawmy jeszcze te same dane na wykresach dla zarządu – ile łącznie trwa proces w zależności od miesiąca?
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
fazy %>% filter(DataKon < today()) %>% # dane agregujemy do miesięcy mutate(DataPocz = make_date(year(DataPocz), month(DataPocz), 1)) %>% # liczymy medianę dla faz w kolejnych miesiącach group_by(DataPocz, Faza) %>% summarise(mCZ = median(CzasTrwania)) %>% ungroup() %>% # sumujemy te mediany dla kolejnych miesięcy group_by(DataPocz) %>% mutate(tCZ = sum(mCZ)) %>% ungroup() %>% ggplot() + # długość trwania fazy w zależności od miesiąca geom_col(aes(DataPocz, mCZ, fill = Faza), color = "gray50") + # długość całego procesu w zależności od miesiąca geom_line(aes(DataPocz, tCZ), size = 2, color = "black") + geom_label(aes(DataPocz, tCZ, label = round(tCZ)), color = "black") + scale_x_date(date_breaks = "1 month", date_labels = "%B") + theme(legend.position = "bottom") + labs(title = "Średnie długości faz w zależności od miesiąca", x = "", y = "Długość fazy", fill = "") |
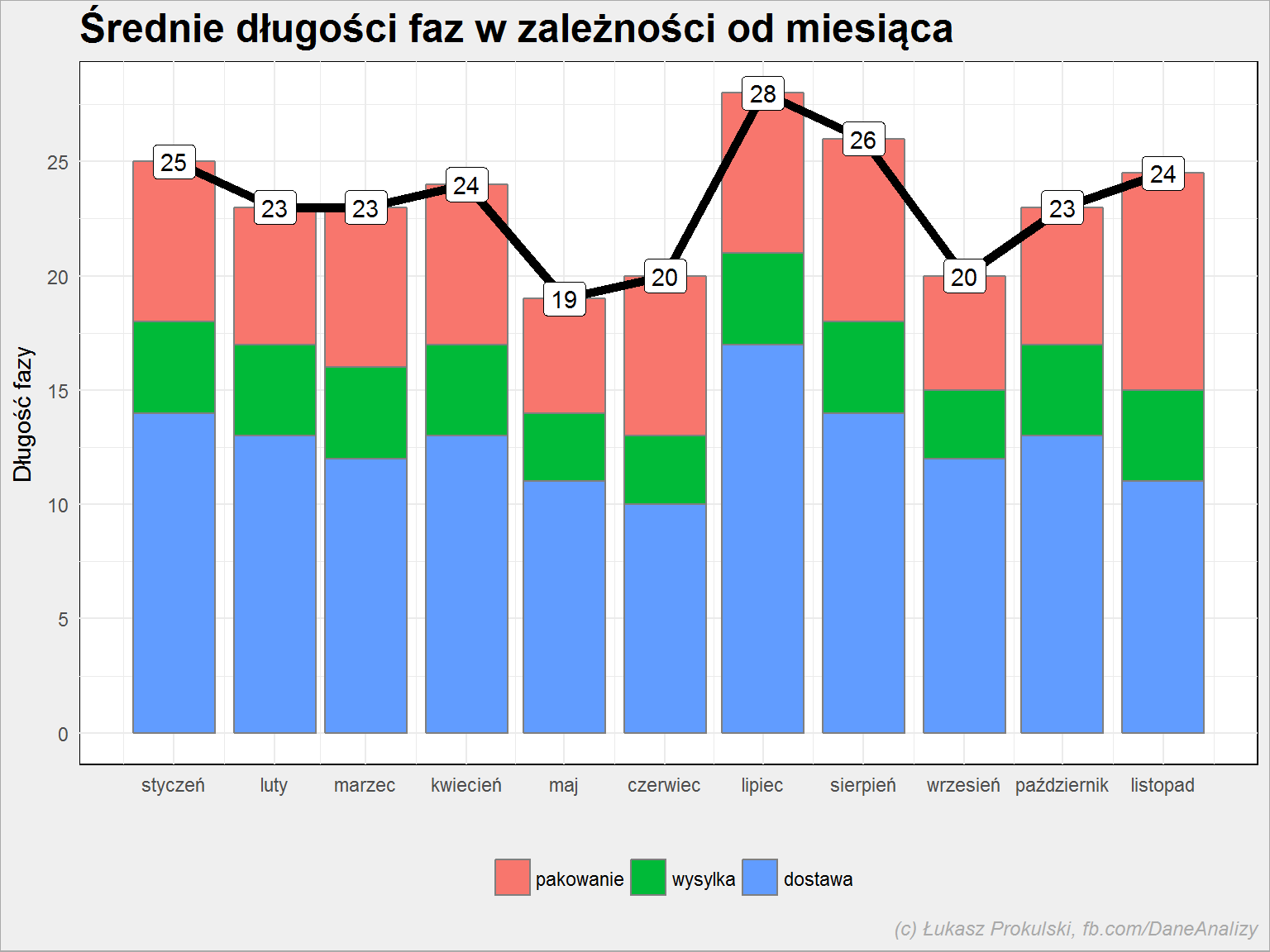
Wykres skumulowany może być mylący, rozdzielmy zatem fazy na oddzielne słupki:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
fazy %>% filter(DataKon < today()) %>% mutate(DataPocz = make_date(year(DataPocz), month(DataPocz), 1)) %>% group_by(DataPocz, Faza) %>% summarise(mCZ = median(CzasTrwania)) %>% ungroup() %>% ggplot() + geom_bar(aes(DataPocz, mCZ, fill = Faza), stat = "identity", position = "dodge", alpha = 0.5, color = "gray50") + geom_line(aes(DataPocz, mCZ, color = Faza), size = 2, show.legend = FALSE) + scale_x_date(date_breaks = "1 month", date_labels = "%B") + theme(legend.position = "bottom") + labs(title = "Średnie długości faz w zależności od miesiąca", x = "", y = "Długość fazy", fill = "") |
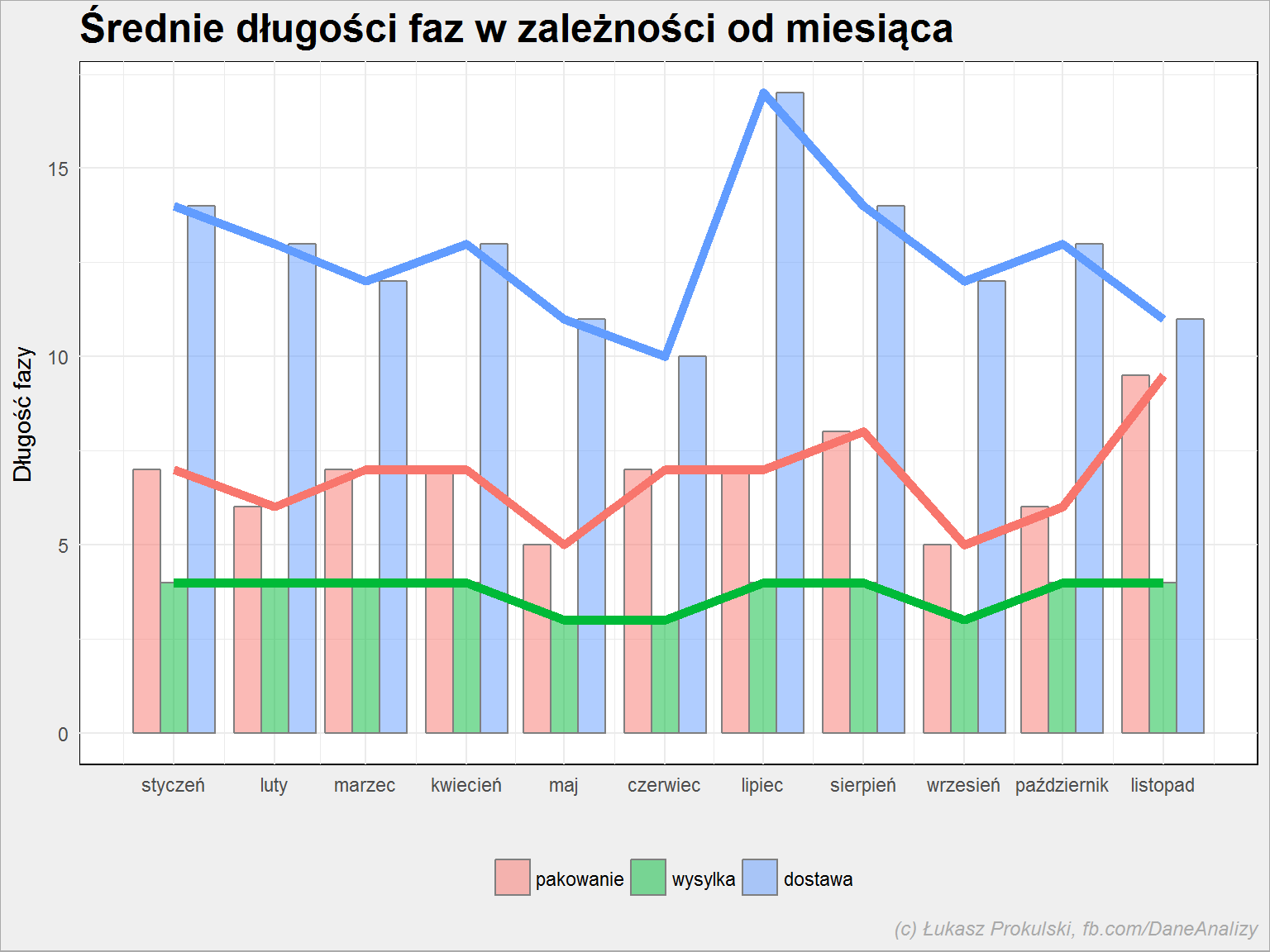
Z obu wykresów (najlepszym rozwiązaniem byłoby dodanie czarnej linii z pierwszego wykresu do wykresu drugiego, być może z osią dodatkową) widać, że w naszym sztucznym sklepie najlepiej zamawiać w maju lub czerwcu. Jako właściciel sklepu szukałbym przyczyn tak długich czasów pakowania (szczególnie w listopadzie) i zastanowił się czy w wakacje nie korzystać z innej firmy kurierskiej.
Tyle tylko, że są to sumy długości poszczególnych faz trwających w danym miesiącu. Pułapka polega na tym, że nie są to czasy oczekiwania na pełną realizację zamówienia. Coś mogło być pakowane w maju, a transportowane w czerwcu – wówczas to samo zamówienie zasili słupek czerwony w maju, a słupek niebieski już w czerwcu. Trzeba policzyć długość procesu dla każdego z zamówień z osobna:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
zamowienia %>% spread(Status, Data) %>% mutate(CzasTrwania = as.numeric(dostawa - zamowienie)) %>% mutate(Data_M = make_date(year(zamowienie), month(zamowienie), 1)) %>% group_by(Data_M) %>% summarise(mCZ = median(CzasTrwania)) %>% ggplot() + geom_col(aes(Data_M, mCZ), fill = "lightgreen", color = "gray50") + geom_label(aes(Data_M, mCZ, label = mCZ), color = "black") + scale_x_date(date_breaks = "1 month", date_labels = "%B") + theme(legend.position = "bottom") + labs(title = "Długości (mediana) reazlizacji zamówienia", x = "Miesiąc złożenia zamówienia", y = "Długość realizacji") |
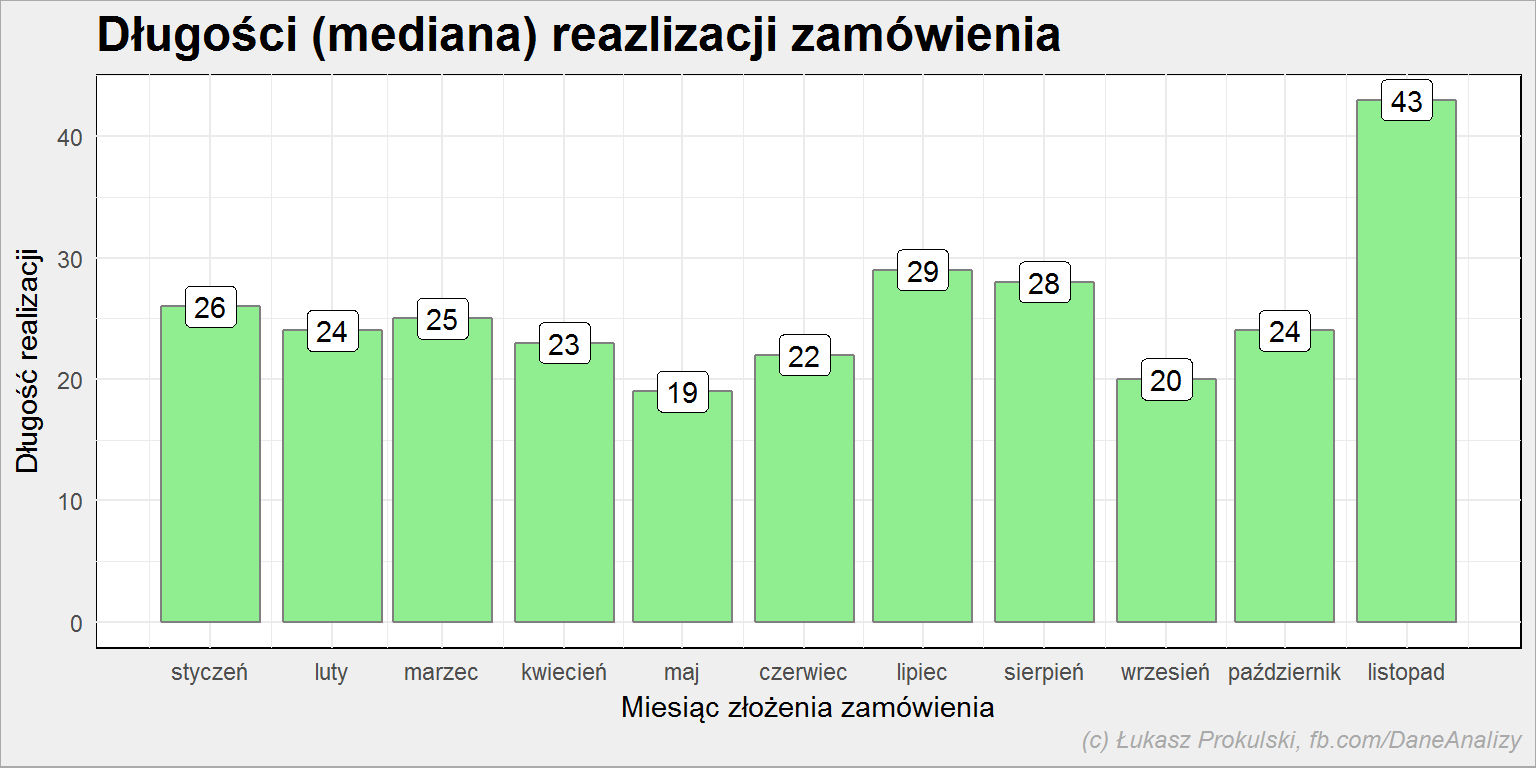
Dane delikatnie się różnią dla całego roku, grudzień jest całkowicie inny. Dodam jeszcze, że mediana czasu realizacji zamówienia dla całego roku to 24 dni, czyli dłużej poczekamy na swój zamówiony towar w wakacje i przed Gwiazdką.
Oby to nie była reguła – zamawiajcie prezenty już teraz!
Super artykuł jak zawsze! Zastanawiamy się też (po drugiej stronie frontu) dlaczego już u nas nie kupują i do których zadzwonić. Pomyślałem, że zainteresuje to Pana: https://joaocorreia.io/blog/rfm-analysis-increase-sales-by-segmenting-your-customers.html bo można pewnie łatwo zrobić w R.
Pingback: Parsowanie XMLa w R | Łukasz Prokulski