Dzisiaj zajmiemy się zagadnieniem zwanym analizą koszykową, która jest jednym z podstawowych narzędzi do badania preferencji zakupowych klientów. Na podstawie wyników można odpowiednio ułożyć produkty w sklepie albo przygotować promocje. Można również przygotować algorytm rekomendacji (“klienci, którzy kupili X kupili też Y”).
Zobaczymy też, że polska kuchnia cebulą stoi. I pieprzem.
Do analizy koszykowej w R wykorzystamy pakiet arules.
|
1 2 3 4 5 |
library(tidyverse) library(stringr) library(reshape2) library(arules) library(arulesViz) |
Teoria
Przed przystąpieniem do analizy potrzebujemy trochę teorii. Wcześniejsze wpisy mówiły o zagadnieniach dość intuicyjnych, ale analiza koszyków wymaga wprowadzenia kilku pojęć.
Ale jeśli nie interesuje Cię teoria, jakieś wskaźniki i całe to programowanie to możesz od razu przeskoczyć do analizy przepisów klikając tutaj.
Koszyk zakupów
Wyobraźmy sobie sklep, w którym można kupić tylko cztery produkty: chleb, mleko, masło i jabłka.
Do tego sklepu przychodzi kolejno 10 osób i każdy kupuje co mu potrzeba, kolejno:
- chleb
- chleb, mleko, masło
- mleko, jabłka
- jabłka
- masło, jabłka
- chleb, masło
- chleb, mleko
- chleb, jabłka
- mleko
- chleb, mleko
Każdy klient to transakcja albo koszyk zakupów.
Zapiszmy to w formie listy w R:
|
1 2 3 4 5 6 7 8 9 10 |
transactions <- list("Chleb", c("Chleb", "Mleko", "Masło"), c("Mleko","Jabłka"), "Jabłka", c("Masło","Jabłka"), c("Chleb","Masło"), c("Chleb","Mleko"), c("Chleb","Jabłka"), "Mleko", c("Chleb","Mleko")) |
Możemy taką listę przerobić na obiekt typu transactions, na którym operuje pakiet arules. Zobaczmy od razu co zawiera taki obiekt w podsumowaniu:
|
1 2 |
trans <- as(transactions, "transactions") summary(trans) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
## transactions as itemMatrix in sparse format with ## 10 rows (elements/itemsets/transactions) and ## 4 columns (items) and a density of 0.45 ## ## most frequent items: ## Chleb Mleko Jabłka Masło (Other) ## 6 5 4 3 0 ## ## element (itemset/transaction) length distribution: ## sizes ## 1 2 3 ## 3 6 1 ## ## Min. 1st Qu. Median Mean 3rd Qu. Max. ## 1.00 1.25 2.00 1.80 2.00 3.00 ## ## includes extended item information - examples: ## labels ## 1 Chleb ## 2 Jabłka ## 3 Masło |
Mamy:
- liczbę transakcji (10) i liczbę produktów (4)
- od razu dostajemy listę najpopularniejszych produktów razem z liczbą koszyków, w których się znalazły
- oraz liczbę produktów w koszykach i jej rozkład (mieliśmy 3 zakupy po 1 produkcie, 6 zakupów po 2 produkty i jeden zakup złożony z trzech produktów)
Teraz możemy sobie na przykład narysować jak wyglądała macierz koszyk-produkt:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
trans@data %>% t() %>% data.matrix() %>% as.data.frame() %>% rename("Chleb" = V1, "Jabłka" = V2, "Masło" = V3, "Mleko" = V4) %>% mutate(trans = row_number()) %>% gather(key = key, value = val, -trans) %>% ggplot() + geom_tile(aes(key, trans, fill=val), color = "black") + scale_fill_manual(values = c("TRUE" = "darkgray", "FALSE" = "white")) + scale_y_continuous(breaks = 1:10, trans = "reverse") + labs(x = "Produkt", y = "Numer transakcji", fill = "Kupiony?") |
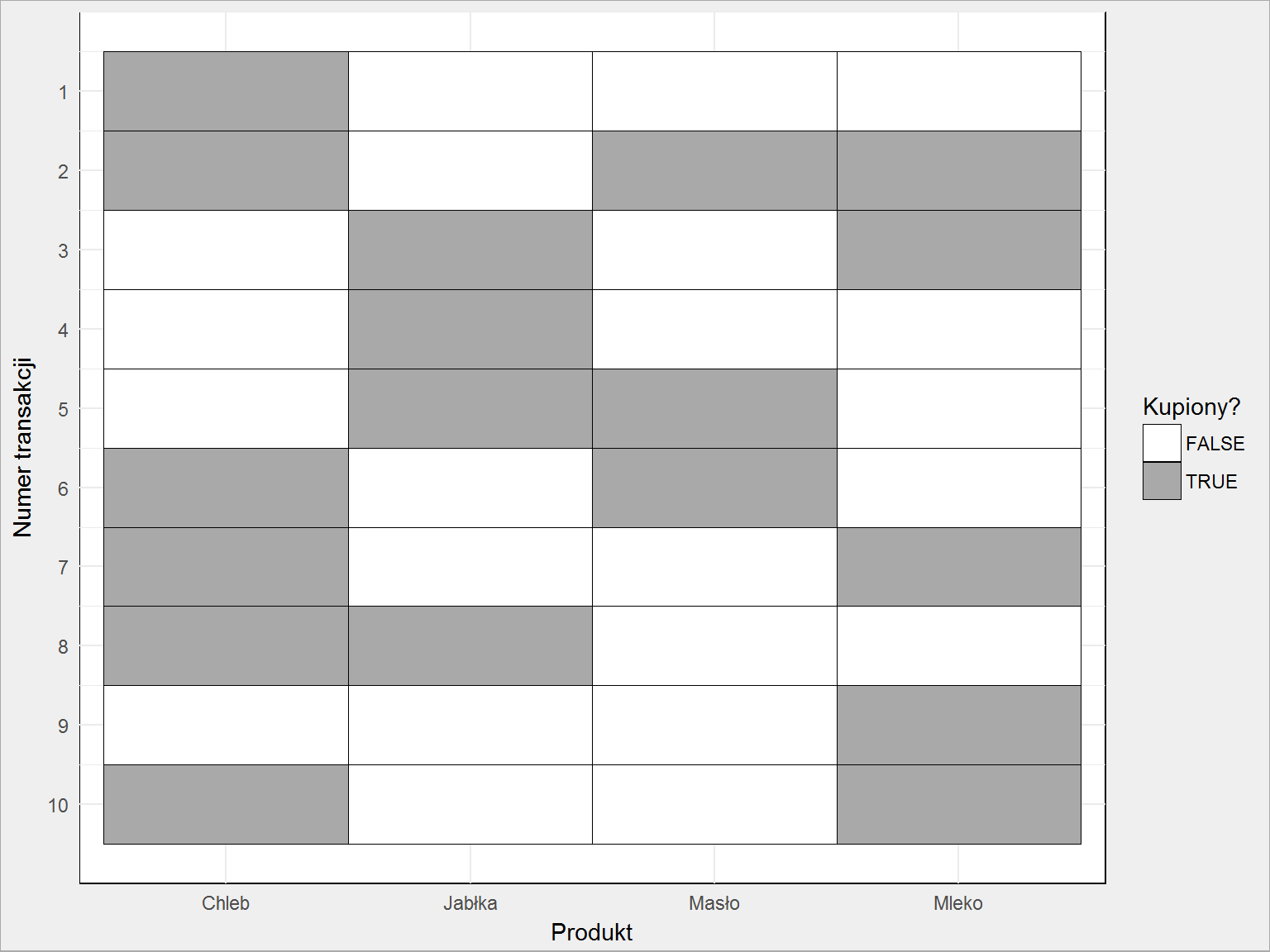
Dość to przekombinowane (ale ładne), w dodatku trzeba znać nazwy poszczególnych produktów i wiedzieć w jakiej kolejności są ułożone (alfabetycznie). To samo można zrobić prościej – potraktować macierz jako obrazek w dwóch kolorach:
|
1 |
image(data.matrix(t(trans@data)), col=c("white", "black")) |
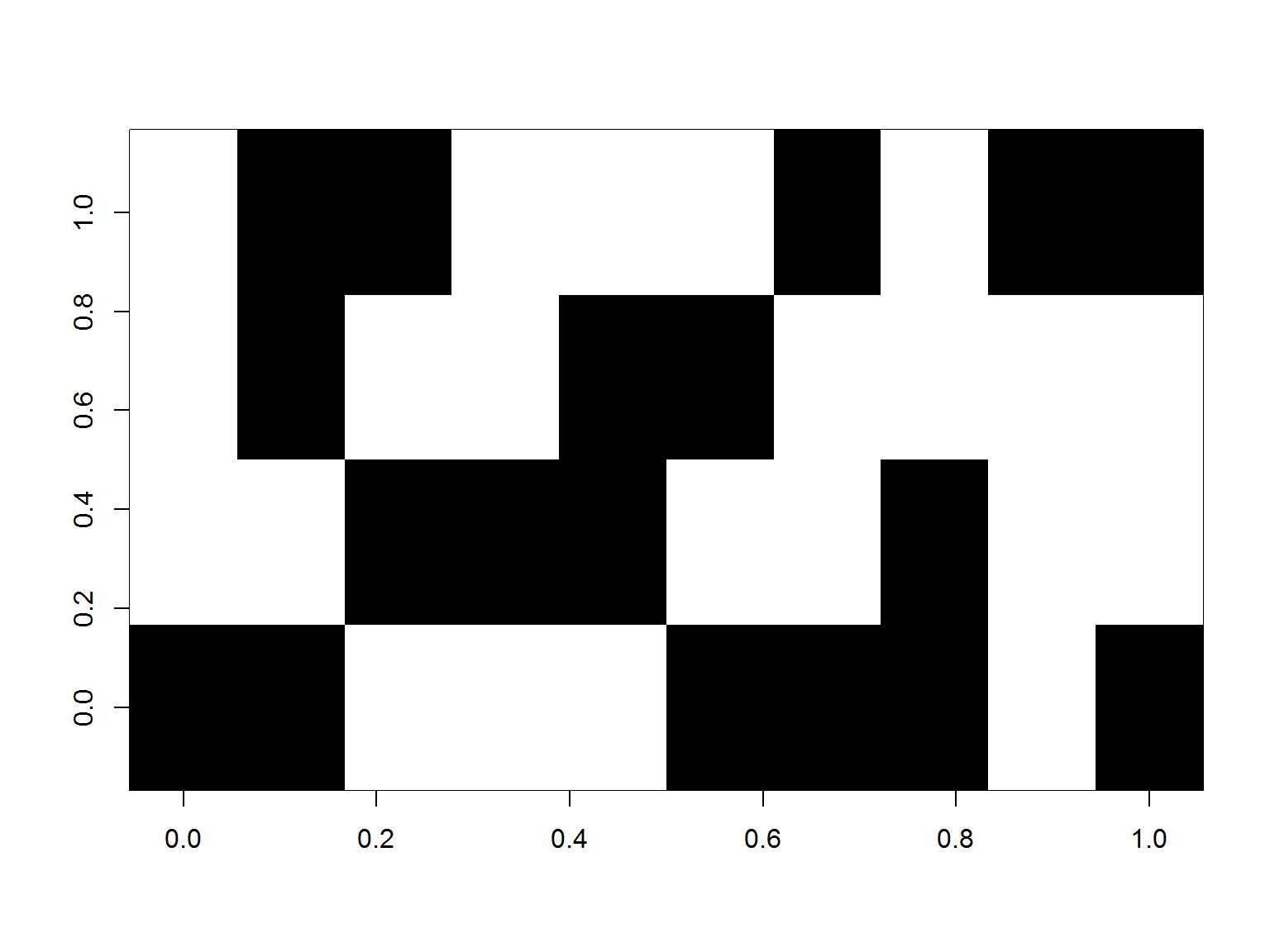
W tym układzie osie są odwrotnie – numery transakcji rosą w prawo.
Oczywiście takie rysowanie ma sens przy małej ilości koszyków i produktów. W pewnym momencie staje się nieczytelne (zobaczycie później, pod koniec wpisu).
Nie daje też właściwie żadnej informacji. Ale zapamiętajcie na chwilę ten obrazek, bo przyda się przy objaśnianiu trzech współczynników (będzie łatwiej liczyć poszczególne kombinacje jako szare pola na obrazku).
Interesuje nas przede wszystkim popularność produktów. W pakiecie arules mamy na to gotową funkcję:
|
1 |
itemFrequencyPlot(trans) |
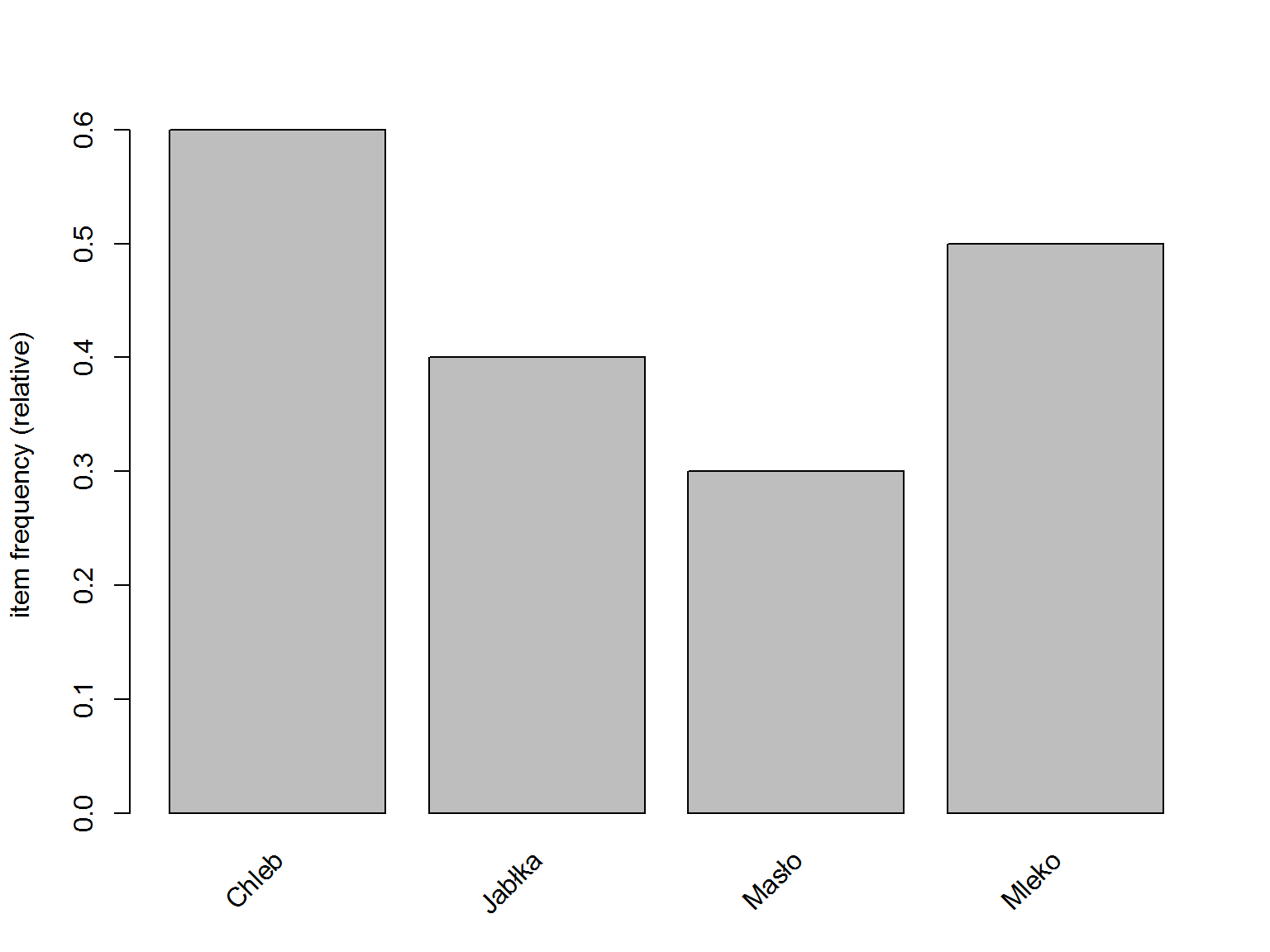
Wszystko zgadza się z tym co dostaliśmy w wyniku działania summary(trans):
- chleb kupiono 6 razy (6/10 = 0.6)
- jabłka 4 razy
- masło 3 razy
- i mleko 5 razy
Można też policzyć szare pola na obrazku (ich liczbę w kolumnie dla każdego z produktów).
Wskaźniki
Liczba (i częstość – znając liczbę koszyków zawierających chleb i liczbę wszystkich koszyków wiemy, że chleb był kupowany w 60% przypadków) to podstawowa miara, ale nie daje wiele informacji, szczególnie o produktach współkupowanych. Częściej kupuje się chleb i masło czy chleb i mleko? A jak ktoś kupił chleb to bardziej prawdopodobne, że dokupi masło czy jednak mleko?
Przy 10 koszykach można to policzyć, ale dla wszystkich transakcji w miesiącu w jakimś hipermarkecie?
Są trzy wskaźniki, które pomogą nam ustalić reguły rządzące koszykami. Skorzystam z angielskich nazw (polskie są jakieś koślawe, a i to co widać w wyniku działania omawianych tutaj funkcji też opisane jest angielskimi nazwami):
Support
![]()
Miara, która mówi o tym jak często dany koszyk t zawierający produkt A (może to być lista produktów) pojawia się we wszystkich transakcjach T. Czyli ile procent klientów kupuje dokładnie te produkty w czasie jednej sesji zakupowej.
Policzyliśmy już każdy produkt oddzielnie, ale ile procent kupuje chleb i mleko, a ile chleb i masło? Kogo jest więcej? Z obrazka już widać, że chleb i mleko pojawia się w koszyku 3 razy (tak więc support = 0.3), a chleb i masło – 2 razy (support = 0.2). Przy okazji jeden z tych razów jest wspólny: koszyk zawiera wszystkie trzy produkty (i dla niego support to 0.1). Oczywiście specjalnie, na potrzeby przykładu.
Confidence
![]()
Ta miara mówi o tym jak często towar A jest kupowany z towarem B (czyli w koszyku są co najmniej A i B). Mleko kupowane razem z chlebem i masłem kupione było dokładnie jeden raz wśród 10 koszyków, albo inaczej na to patrząc – jeden z dwóch koszyków zawierających chleb i masło zawierał też mleko (confidence = 0.5).
Lift
To miara która mówi o swego rodzaju “wzmocnieniu” zakupu produktu B przez produkt A. Definiowana jest jako:
![]()
Jeśli wartość lift jest równa jeden dla danej reguły to prawdopodobieństwo wystąpienia poprzednika (produkt A) i konsekwencji (produkt B) są niezależne od siebie. Nie można wówczas wyciągnąć żadnego wniosku o współkupowalności produktów A i B.
Dla lift > 1, lift określa stopień w jakim zdarzenia są od siebie zależne, co daje nam miernik współkupowalności produktów.
Spójrzmy na nasze 10 koszyków i wartości poszczególnych wskaźników.
Najpierw musimy przygotować odpowiednie reguły – czyli całą analizę. “Całą analizę” oznacza na szczęście wywołanie jednej funkcji:
|
1 2 3 4 |
itemsets <- apriori(trans, parameter = list(supp = 0.01, conf = 0.01, target = "rules")) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
## Apriori ## ## Parameter specification: ## confidence minval smax arem aval originalSupport maxtime support minlen ## 0.01 0.1 1 none FALSE TRUE 5 0.01 1 ## maxlen target ext ## 10 rules FALSE ## ## Algorithmic control: ## filter tree heap memopt load sort verbose ## 0.1 TRUE TRUE FALSE TRUE 2 TRUE ## ## Absolute minimum support count: 0 ## ## set item appearances ...[0 item(s)] done [0.00s]. ## set transactions ...[4 item(s), 10 transaction(s)] done [0.00s]. ## sorting and recoding items ... [4 item(s)] done [0.00s]. ## creating transaction tree ... done [0.00s]. ## checking subsets of size 1 2 3 done [0.00s]. ## writing ... [19 rule(s)] done [0.00s]. ## creating S4 object ... done [0.00s]. |
Widzimy, że powstało 19 reguł. Parametry supp oraz conf mówią o minimalnych wartościach dla Support i Confidence – tutaj dobrane są tak, aby załapały się wszystkie koszyki. Ale przy ogromnych wolumenach danych trzeba je dobrać rozsądnie.
Spójrzmy na wszystkie reguły jakie zostały wyliczone:
|
1 |
inspect(itemsets) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
## lhs rhs support confidence lift ## [1] {} => {Masło} 0.3 0.3000000 1.0000000 ## [2] {} => {Jabłka} 0.4 0.4000000 1.0000000 ## [3] {} => {Mleko} 0.5 0.5000000 1.0000000 ## [4] {} => {Chleb} 0.6 0.6000000 1.0000000 ## [5] {Masło} => {Jabłka} 0.1 0.3333333 0.8333333 ## [6] {Jabłka} => {Masło} 0.1 0.2500000 0.8333333 ## [7] {Masło} => {Mleko} 0.1 0.3333333 0.6666667 ## [8] {Mleko} => {Masło} 0.1 0.2000000 0.6666667 ## [9] {Masło} => {Chleb} 0.2 0.6666667 1.1111111 ## [10] {Chleb} => {Masło} 0.2 0.3333333 1.1111111 ## [11] {Jabłka} => {Mleko} 0.1 0.2500000 0.5000000 ## [12] {Mleko} => {Jabłka} 0.1 0.2000000 0.5000000 ## [13] {Jabłka} => {Chleb} 0.1 0.2500000 0.4166667 ## [14] {Chleb} => {Jabłka} 0.1 0.1666667 0.4166667 ## [15] {Mleko} => {Chleb} 0.3 0.6000000 1.0000000 ## [16] {Chleb} => {Mleko} 0.3 0.5000000 1.0000000 ## [17] {Masło,Mleko} => {Chleb} 0.1 1.0000000 1.6666667 ## [18] {Chleb,Masło} => {Mleko} 0.1 0.5000000 1.0000000 ## [19] {Chleb,Mleko} => {Masło} 0.1 0.3333333 1.1111111 |
Jeśli kolumna lhs jest pusta oznacza to, że w koszyku był tylko jeden produkt. I to się zgadza z tym co policzyliśmy wcześniej (teraz przyda się przypomnienie sobie obrazka) – 3/10 razy masło, 4/10 razy jabłka itd. Można ograniczyć tworzenie reguł do określonej minimalnej liczby produktów – służy do tego parametr minlen.
Ale już jeśli ktoś kupił masło to mógł mieć w koszyku też jabłka (reguła numer 5). Support = 0.1, czyli 1 z 10 transakcji tak właśnie wyglądała. Rzut oka na obrazek i widzimy, że to transakcja numer 5. Oczywiście działa to tak samo w drugą stronę – mając jabłka kupiliśmy masło (reguła 6). Nie znamy kolejności wkładania produktów do koszyka, zatem reguły są symetryczne.
Zobaczmy na Confidence. Wiersz 10 – Chleb => Masło. 2/10 (wartość support) takich transakcji, zgadza się. W koszyku chleb pojawił się 6 razy, z czego razem z masłem 2 razy (transakcje 2 oraz 6). Czyli w 1/3 = 0.333 przypadków. Można więc powiedzieć, że kupienie chleba w 33% oznacza również kupno masła (“33% klientów którzy kupili chleb, kupili też masło”).
Dla sytuacji odwrotnej (Masło => Chleb) mamy confidence na poziomie 66% (3 koszyki z masłem, w tym 2 też z chlebem).
Ostatni współczynnik to Lift.
Interesują nas reguły z lift > 1. Największą wartość lift ma reguła 17 (Masło, Mleko => Chleb). Widzimy, że jeśli ktoś kupił jednocześnie masło i mleko kupił też chleb. Spójrzmy na regułę 19 (Chleb, Mleko => Masło). Chleb i mleko mamy w trzech koszykach (2, 7 i 10), z czego dodatkowo masło jest w koszyku 2 (stąd confidence dla reguły 19 równe 1/3). Lift jest większy od jedynki, co oznacza że prawdopodobne jest kupienie masła jeśli już w koszyku mamy chleb i mleko. Im większy lift tym większe to prawdopodobieństwo.
Pakiet arules pozwala na policzenie jeszcze kilkunastu innych miar – polecam dokumentację dla funkcji interestMeasure().
Uzbrojeni w taką wiedzę możemy przejść do realnego świata. Nie mamy co prawda danych o zakupach (och, jakże bym chciał mieć taki wyciąg z kasy fiskalnej jakiegoś sklepu! Kto podeśle?), ale jest coś analogicznego. Bo transakcjami może być wszystko. W pakiecie arules mamy zaszyte dane Income (transakcje) oraz IncomeESL (to samo w formie data frame). Są to dane demograficzne z 8993 ankiet zawierające 14 cech.
My jednak zajmiemy się czymś innym.
Praktyka – przepisy kulinarne
Każdy przepis składa się z produktów. Zatem jest swego rodzaju koszykiem z zakupami, prawda? Bingo! To znajdźmy sobie dużo przepisów, tak żeby zobaczyć jakie produkty są potrzebne…
Pobranie danych
Skąd wziąć dane? Jest sobie serwis Ugotuj.to (który kiedyś, w jakiejś wcześniejszej wersji projektowałem jako UX desinger) zawierający masę przepisów z jedną bardzo fajną charakterystyczną cechą. W większości przepisów wśród składników znajdziemy linki do strony ze składnikiem podstawowym (za moich czasów w Ugotuju tego nie było). Dzięki temu pozbędziemy się problemu odmiany słów (jedna cebula, dwie cebule, pół cebuli, dwa ziemniaki, jeden ziemniak, pół kilo ziemniaków) – wykorzystamy link do strony składników podstawowych.
Jeśli nie interesują Cię technikalia pobierania danych i całe to programowanie – możesz przeskoczyć do analizy przepisów klikając tutaj
Lista wszystkich przepisów
Najpierw potrzebujemy listy wszystkich przepisów. Tak się znakomicie składa, że Ugotuj.to posiada taką listę! Na kolejnych stronach są kolejne linki do przepisów. Trzeba tylko przejechać przez wszystkie strony i wyciągnąć URLe do pełnych przepisów.
Żeby oszczędzić serwery Ugotuj.to oraz nie narazić się na szybkie zbanowanie wykorzystamy sztuczkę, którą znalazłem na blogu Maëlle (w ślad za rud.is). Cały poniższy kod można zapisać w jednym skrypcie i uruchomić tylko raz.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
library(rvest) library(tidyverse) library(stringr) # taka sztuczka z pakietu purrr - "bezpieczna" (bez wyrzucania błędów) # wersja funkcji read_html safe_read_html <- safely(read_html) # miejsce na URLe przepisów ugotuj_urls_all <- vector() # 751 to liczba stron indeksu z listą przepisów for(i in 1:751) { page_url <- paste0("http://ugotuj.to/ugotuj/", i) page <- safe_read_html(page_url) # safe_read_html w przypadku błędu read_html zwróci wartość błędu w polu error if(is.null(page$error)) { # jeśli nie ma błędu - wartość zwrócona przez read_html znajdzie się w polu result ugotuj_urls <- page$result %>% html_node("div#holder_217") %>% html_node("article.mod_product_index2") %>% html_node("ul") %>% html_nodes("li.entry") %>% html_node("div.content") %>% .[!is.na(.)] %>% html_node("h2") %>% html_node("a") %>% html_attr("href") # doklejamy kolejny url ugotuj_urls_all <- c(ugotuj_urls_all, ugotuj_urls) } # czekamy chwilkę, żeby nie zabić serwerów i nie wzbudzić podejrzeń ;) Sys.sleep(sample(seq(0.25, 1.5, 0.25), 1)) } # nie bierzemy przepisów o ujemnych ID # nie mają tego co potrzebujemy, szkoda na nie prądu ;) ugotuj_urls_all <- ugotuj_urls_all[!grepl("/ugotuj/-", ugotuj_urls_all, fixed = TRUE)] ugotuj_urls_all <- unique(ugotuj_urls_all) saveRDS(ugotuj_urls_all, file = "ugotuj_urls_all.rds") |
Wynik to lista adresów URL do przepisów zapisana w pliku ugotuj_urls_all.rds
Treści przepisów
Skorzystamy teraz z tego pliku i pobierzemy kolejne przepisy. Znowu – skrypt uruchamiamy raz, a w wyniku mamy pliki z danymi
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
library(rvest) library(tidyverse) library(stringr) # lista URLi do przepisów ugotuj_urls_all <- readRDS("ugotuj_urls_all.rds") # ile przepisów musimy pobrać? max_n <- length(ugotuj_urls_all) # bezpieczna wersja read_html safe_read_html <- safely(read_html) # miejsce na pełne dane o przepisach przepisy_all <- data_frame() for(i in 1:max_n) { # dla każdego urla do przepisu page_url <- paste0("http://ugotuj.to", ugotuj_urls_all[i]) # pobieramy stronę page <- safe_read_html(page_url) if(is.null(page$error)) { # jeśli nie ma błędów - wyciągamy potrzebne informacje art <- page$result %>% html_nodes("div#art") %>% html_node("div#artykul") tytul <- art %>% html_node("span.txt_srodtytul") %>% html_node("span") %>% html_text() skladniki <- art %>% html_node("div.recipe") %>% html_node("ul") %>% html_nodes("li") %>% html_node("span") %>% html_node("a") %>% html_attr("href") %>% str_replace_all("/ugotuj/skladniki_podst-", "") skladniki <- skladniki[!is.na(skladniki)] przepisy_all <- bind_rows(przepisy_all, data_frame(n = rep(i, length(skladniki)), tytul = rep(tytul, length(skladniki)), skladniki = skladniki, url = rep(page_url, length(skladniki)))) } # chwilkę czekamy Sys.sleep(sample(seq(0.25, 1.5, 0.25), 1)) } # zapisujemy zebrane dane saveRDS(przepisy_all, file = "przepisy_all.rds") |
Na początek musimy wyczyścić sobie nieco dane (można było to zrobić na etapie ich zbierania). Mamy zapisane pliki, możemy więc zacząć od zera:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
library(tidyverse) library(stringr) library(reshape2) library(arules) library(arulesViz) rm(list = ls()) # wczytujemy nasze przepisy przepisy_all <- readRDS("przepisy_all.rds") # usunięcie duplikatów i śmieci przepisy_all <- przepisy_all %>% # poprawka w nazwach składników mutate(skladniki = gsub("<a href=", "", skladniki, fixed = TRUE)) %>% mutate(skladniki = gsub("+", " ", skladniki, fixed = TRUE)) %>% mutate(skladniki = gsub("?", "", skladniki, fixed = TRUE)) %>% distinct() %>% filter(nchar(skladniki) != 0) |
Teraz możemy zacząć zabawę!
Analiza przepisów
Zaczniemy standardowo, bez wykorzystania narzędzi do analizy koszyków.
Najpopularniejsze składniki w przepisach
Jakie są najpopularniejsze składniki przepisów? Zobaczmy top 30:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
przepisy_all %>% count(skladniki) %>% ungroup() %>% mutate(p = 100 * nn / sum(nn)) %>% top_n(30, wt = p) %>% arrange(p) %>% mutate(skladniki = factor(skladniki, levels = skladniki)) %>% ggplot() + geom_bar(aes(skladniki, p, fill=skladniki), stat="identity", color = "black", show.legend = FALSE) + labs(x = "Składnik", y = "% przepisów", title = "Najpopularniejsze składniki przepisów") + coord_flip() |
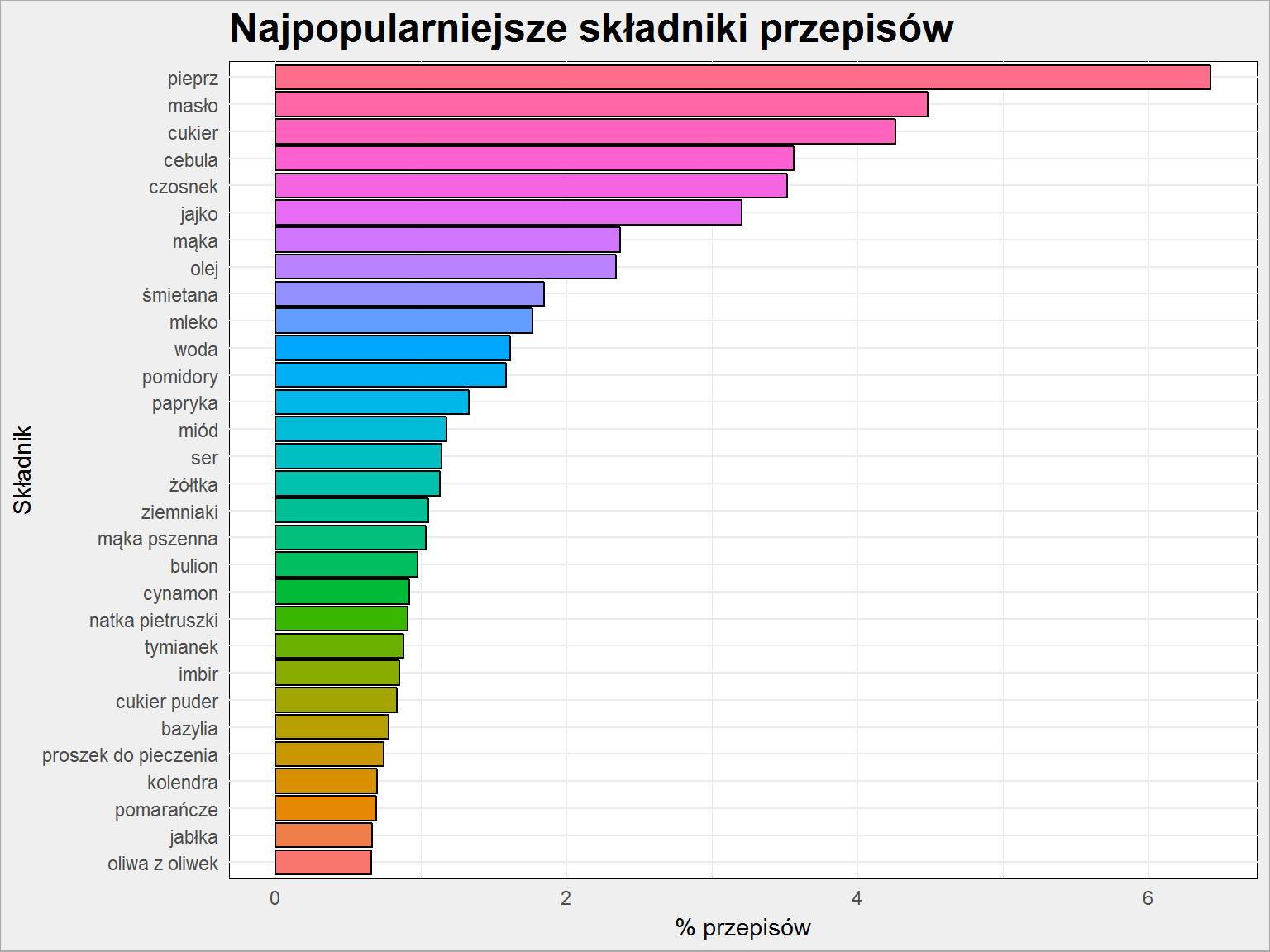
Pieprz jak najbardziej. Soli nie ma, bo nie jest wyróżniona w przepisach jako składnik podstawowy. Szkoda, bo nie dowiemy się tym sposobem czy jest bardziej popularna niż pieprz…
Wysoka pozycja masła nie powinna dziwić: używa się go do smażenia (stąd też wysoko olej) ale też do pieczenia. Podobniej jest z cebulą i czosnkiem: występują właściwie w każdej potrawie obiadowej (ale jak widać tylko w około 3.5% przepisów).
Co się z czym łączy?
Jakie kombinacje składników (dwóch) są najpopularniejsze? Pieprz i sól? Wiemy, że o soli się nie dowiemy…
Najpierw przygotujemy odpowiednią tabelę (układ danych wymaga nieco gimnastyki):
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
skladniki_polaczenia <- przepisy_all %>% select(n, skladniki) %>% # podziel po numerze przepisu slice_rows("n") %>% # dla kazdej grupy macierz kazdy-kazdy by_slice(~ dcast(., formula = skladniki ~ skladniki, fun.aggregate = length, value.var = "skladniki") %>% # pivot macierzy melt(id.vars = "skladniki", value.name = "value") %>% # bez przeciątnej macierzy (bez sam ze sobą) filter(skladniki != variable) %>% mutate(value = 1), .collate = "list") %>% # wynikowe mikrotabelki złącz w jedną dużą bind_rows(.$.out) %>% select(skladniki, variable, value) %>% filter(!is.na(value)) # posumuj pary składników skladniki_polaczenia <- skladniki_polaczenia %>% mutate(prod_a = ifelse(skladniki < variable, skladniki, variable), prod_b = ifelse(skladniki < variable, variable, skladniki)) %>% select(prod_a, prod_b, n = value) %>% group_by(prod_a, prod_b) %>% summarise(n = sum(n)) %>% ungroup() %>% distinct() |
Dla czytelności wykresu weźmy tylko najpopularniejszy 1% połączeń:
|
1 2 3 4 5 6 7 8 9 10 11 |
skladniki_polaczenia %>% filter(n >= quantile(n, 0.99)) %>% ggplot() + geom_tile(aes(prod_a, prod_b, fill=n)) + theme(axis.text.x = element_text(angle = 90, hjust=1, vjust=0)) + scale_fill_gradient2(low = "green", mid = "yellow", high = "red", midpoint = 3000) + labs(x = "", y = "", fill = "Liczba przepisów, w których składniki występują razem", title = "Najpopularniejsze połączenia składników", subtitle = "(1% najpopularniejszych połączeń)") + theme(legend.position = "bottom") |
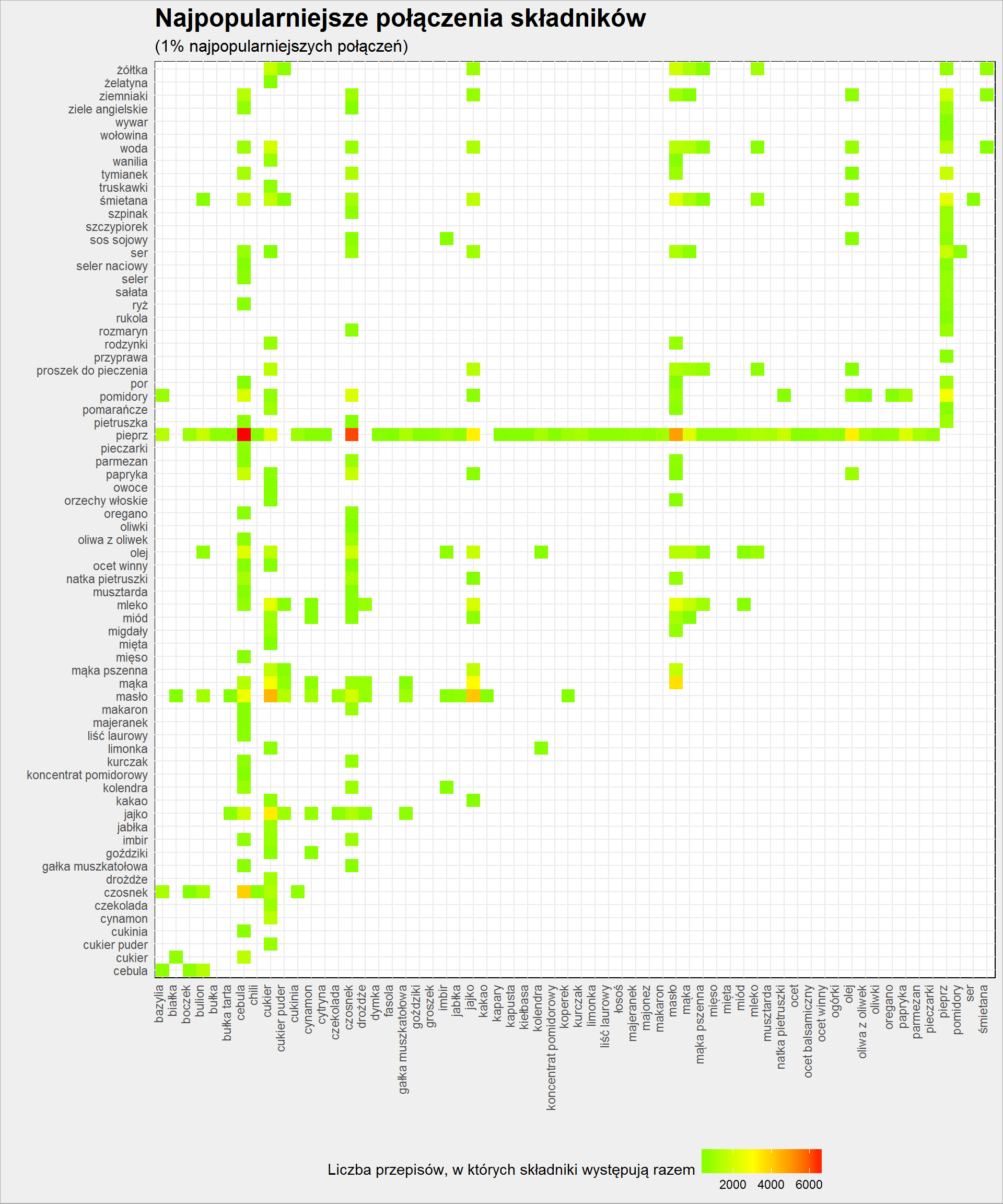
Jak widać pieprz łączy się właściwie ze wszystkim.
Najpopularniejsze połączenia to pieprz z cebulą lub czosnkiem, nieco mniej z masłem lub olejem. Dominują kombinacje pieprz, cebula, czosnek, masło, olej. Do tego dochodzą pomidory, które lubią pieprz, cebulę i czosnek.
Inna kategoria ciekawych i popularnych połączeń to kombinacje jajka, mąki, masła i cukru. Kto wie co to? Myślimy, myślimy i wiemy.
Trzydzieści najpopularniejszych połączeń to:
|
1 2 3 |
skladniki_polaczenia %>% top_n(30, wt = n) %>% arrange(desc(n)) |
| prod_a | prod_b | n |
|---|---|---|
| cebula | pieprz | 6650 |
| czosnek | pieprz | 6234 |
| masło | pieprz | 4862 |
| cukier | masło | 4444 |
| jajko | masło | 4112 |
| cebula | czosnek | 3942 |
| masło | mąka | 3622 |
| cukier | jajko | 3360 |
| olej | pieprz | 3302 |
| jajko | pieprz | 3254 |
| jajko | mąka | 3056 |
| pieprz | pomidory | 2750 |
| cukier | mąka | 2716 |
| cebula | masło | 2592 |
| masło | mleko | 2456 |
| cukier | mleko | 2362 |
| pieprz | śmietana | 2328 |
| masło | śmietana | 2232 |
| mąka | pieprz | 2210 |
| cebula | olej | 2206 |
| cukier | pieprz | 2200 |
| papryka | pieprz | 2178 |
| czosnek | pomidory | 2168 |
| cebula | pomidory | 2050 |
| jajko | mleko | 2046 |
| czosnek | masło | 1960 |
| cukier | woda | 1886 |
| czosnek | olej | 1886 |
| cebula | jajko | 1810 |
| pieprz | ziemniaki | 1806 |
Kiedy popatrzymy na wszystkie połączenia:
|
1 2 3 4 5 6 7 8 9 |
skladniki_polaczenia %>% ggplot() + geom_tile(aes(prod_a, prod_b, fill=n)) + theme(axis.text.x = element_text(angle = 90, hjust=1, vjust=0)) + scale_fill_gradient2(low = "green", mid = "yellow", high = "red", midpoint = 3000) + labs(x = "Składnik A", y = "Składnik B") + theme(axis.text.x = element_blank(), axis.text.y = element_blank(), legend.position = c(0.9, 0.2)) |
Widzimy, że są pewne produkty, które łączą się z prawie wszystkim, ale są też białe plamy.
Mając tak przygotowane dane możemy zobaczyć
z czym najczęściej występuje dany produkt
Weźmy jakiś zakręcony, na przykład ciecierzycę:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# jaki produkt? produkt_a = "ciecierzyca" skladniki_polaczenia %>% filter(prod_a == produkt_a | prod_b == produkt_a) %>% mutate(produkt = ifelse(prod_a == produkt_a, prod_b, prod_a)) %>% top_n(20, wt = n) %>% arrange(n) %>% mutate(produkt = factor(produkt, levels = produkt)) %>% ggplot() + geom_bar(aes(produkt, n, fill=produkt), stat="identity", color = "black", show.legend=FALSE) + coord_flip() + labs(x = "Składnik", y="Liczba przepisów", title = paste0("Z czym najczęściej występuje ", produkt_a, "?"), subtitle = "20 najpopularniejszych składników") |
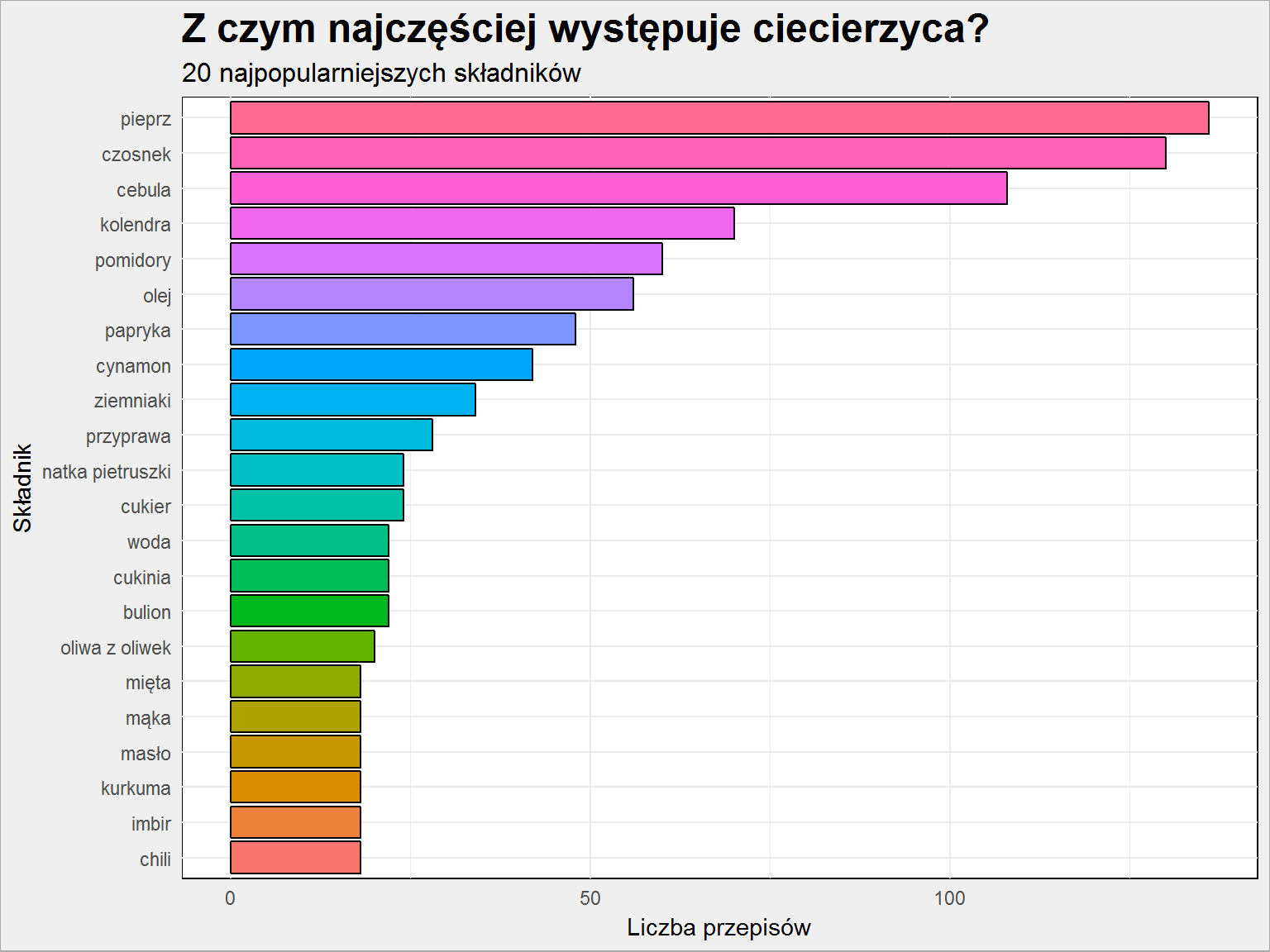
Na początku oczywiście pieprz, czosnek i cebula – te występują prawie zawsze. Ale jak widać ciecierzyca doprawiana jest kolendrą albo cynamonem.
Powyższy fragment kodu jest na tyle uniwersalny, że bardzo łatwo możecie znaleźć najdziwniejsze produkty, wystarczy odpowiednio ustawić wartość zmiennej produkt_a.
Co można ugotować mając…
Zobaczmy co możemy ugotować mając jakieś produkty w lodówce. Odwieczny problem studenta: co zrobić z parówek, żółtego sera i jednego jajka?
Dla całej listy posiadanych składników przejdziemy po kolei listę przepisów zawężając ją do przepisów zawierających dany składnik. Później tę zawężoną listę przechodzimy ponownie i zawężamy dla drugiego składnika. I tak składnik po składniku.
Dla przykładu poszukajmy przepisów, w których występuje limonka, makaron ryżowy oraz sos rybny:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
sklad <- c("limonka", "makaron ryżowy", "sos rybny") # lista wyjściowa - wszystkie przepisy lista_przepisy <- przepisy_all # dla kolejnych składników z listy: for(i in 1:length(sklad)) { # wybierz numery przepisów, gdzie jest i-ty składnik n_lista_przepisy <- lista_przepisy %>% filter(skladniki == sklad[i]) %>% select(n) # z listy przepisów wybierz te z odpowiednimi numerami lista_przepisy <- lista_przepisy %>% filter(n %in% n_lista_przepisy$n) # dalsze operacje rób na tej wybranej liście (kolejne zawężenia) } |
Sprawdźmy co nam zostało?
|
1 2 3 4 5 6 7 8 9 10 11 12 |
lista_przepisy %>% select(-n) %>% # policzmy ile potrzeba składników group_by(url) %>% mutate(n_skladnikow = n()) %>% ungroup() %>% # nie będziemy pokazywać składników select(-skladniki) %>% distinct() %>% # wg ilości składników arrange(n_skladnikow) %>% select(tytuł, url, n_skladnikow) |
Graf
Widzieliśmy, że wśród par składników pojawiają się produkty związane ze smażeniem większości mięs (olej, masło, pieprz, cebula i czosnek) oraz coś co może sugerować wypieki (masło, jajka, mąka, cukier). Spróbujmy używając grafów skategoryzować produkty na grupy.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
library(igraph) # tylko 5% najpopularniejszych połączeń graph_data <- skladniki_polaczenia %>% filter(n >= quantile(n, 0.95)) graph <- graph_from_data_frame(graph_data) # liczba połączeń jako waga krawędzi E(graph)$weigth = graph_data$n # spróbujmy znaleźć grupy wc <- walktrap.community(graph) V(graph)$membership <- wc$membership # metoda rozłożenia węzłów grafu graph_lay <- layout_with_kk(graph) # rysujemy graf plot(graph, # właściwości wyglądu wierzchołków grafu vertex.size = 2, vertex.label.cex = 0.9, # kolor na podstawie grup vertex.color = V(graph)$membership, vertex.label.color = V(graph)$membership, # grubość krawędzi na podstawie popularności połączeń produktów edge.width = 5*E(graph)$weigth/max(E(graph)$weigth), edge.color = "lightgray", edge.arrow.size = 0, layout = graph_lay) |
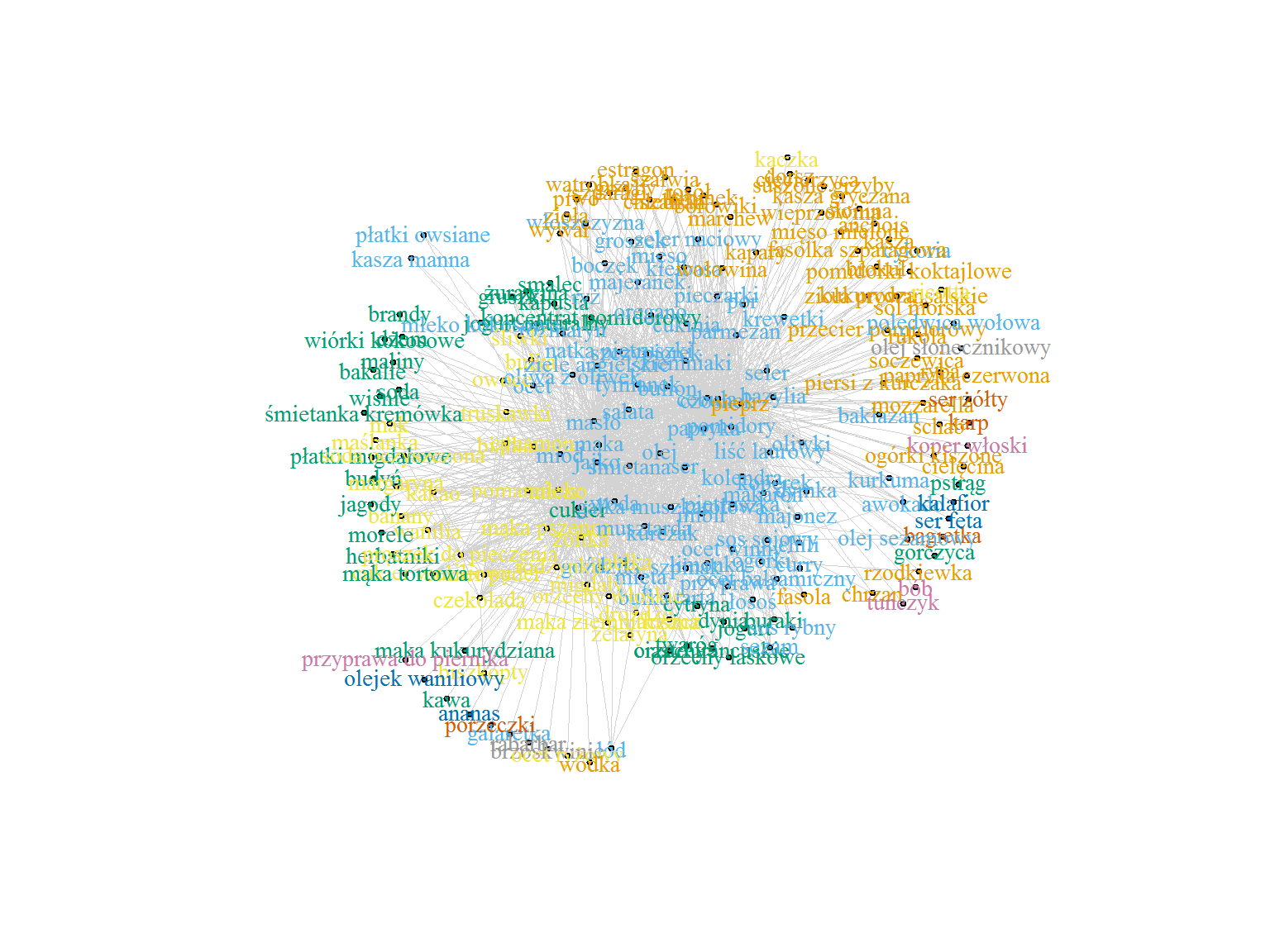
Widać, że jeden kolor to produkty okołoowocowe (lewa strona grafu), inny – mięso (prawa strona), w środku mamy przyprawy, olej, masło i mąkę.
Analiza koszykowa przepisów kulinarnych
Wróćmy do tematu przewodniego dzisiejszego postu – czy podobne informacje uda się uzyskać za pomocą analizy koszykowej?
Na początek potrzebujemy listy transakcji (koszyków). Za koszyk uznamy składniki pojedynczego przepisu.
|
1 2 3 4 5 6 7 |
skladniki_all <- przepisy_all %>% slice_rows("n") %>% by_slice(~ unlist(.$skladniki), .collate="list") %>% .$.out trans <- as(skladniki_all, "transactions") summary(trans) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
## transactions as itemMatrix in sparse format with ## 17123 rows (elements/itemsets/transactions) and ## 394 columns (items) and a density of 0.01831953 ## ## most frequent items: ## pieprz masło cukier cebula czosnek (Other) ## 7944 5540 5263 4400 4343 96102 ## ## element (itemset/transaction) length distribution: ## sizes ## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 ## 160 511 1023 1556 2003 2294 2247 2034 1695 1272 859 522 368 250 148 ## 16 17 18 19 20 21 22 23 24 ## 82 34 32 9 11 5 4 1 3 ## ## Min. 1st Qu. Median Mean 3rd Qu. Max. ## 1.000 5.000 7.000 7.218 9.000 24.000 ## ## includes extended item information - examples: ## labels ## 1 agrest ## 2 algi ## 3 amarantus |
Mamy ponad 17 tysięcy przepisów (zgadza się – tyle było URLi do przepisów), a najpopularniejsze produkty to pieprz, masło, cukier, cebula i czosnek. Widać to też na wykresie (porównajcie go z tym wcześniejszym):
|
1 |
itemFrequencyPlot(trans, topN = 30) |
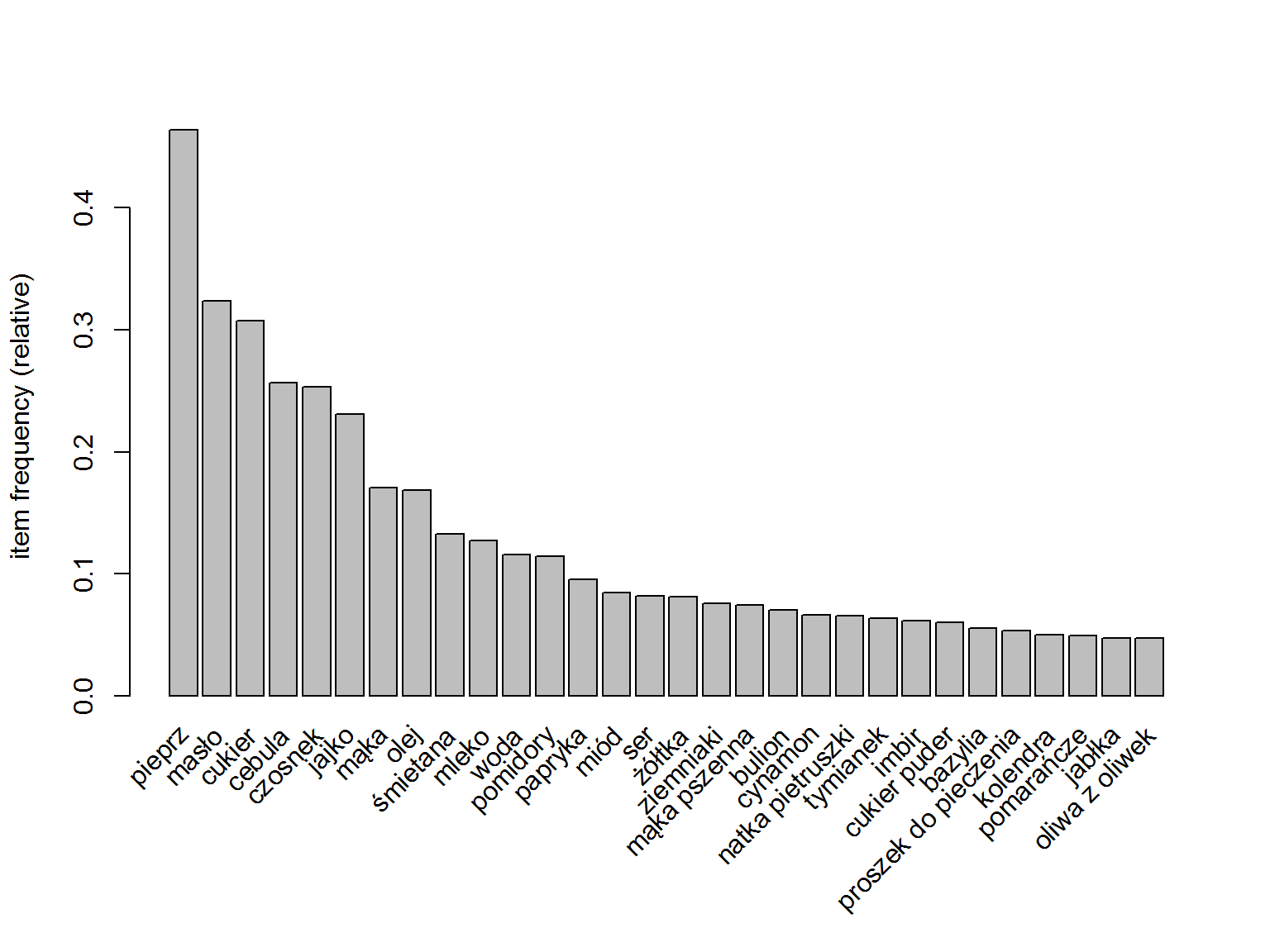
Kolejność produktów jest taka sama jak na wykresie stworzonym wcześniej.
Zobaczmy jeszcze to co robiliśmy na początku – heatmapę reguł i produków:
|
1 |
image(data.matrix(t(trans@data)), col=c("white", "black")) |
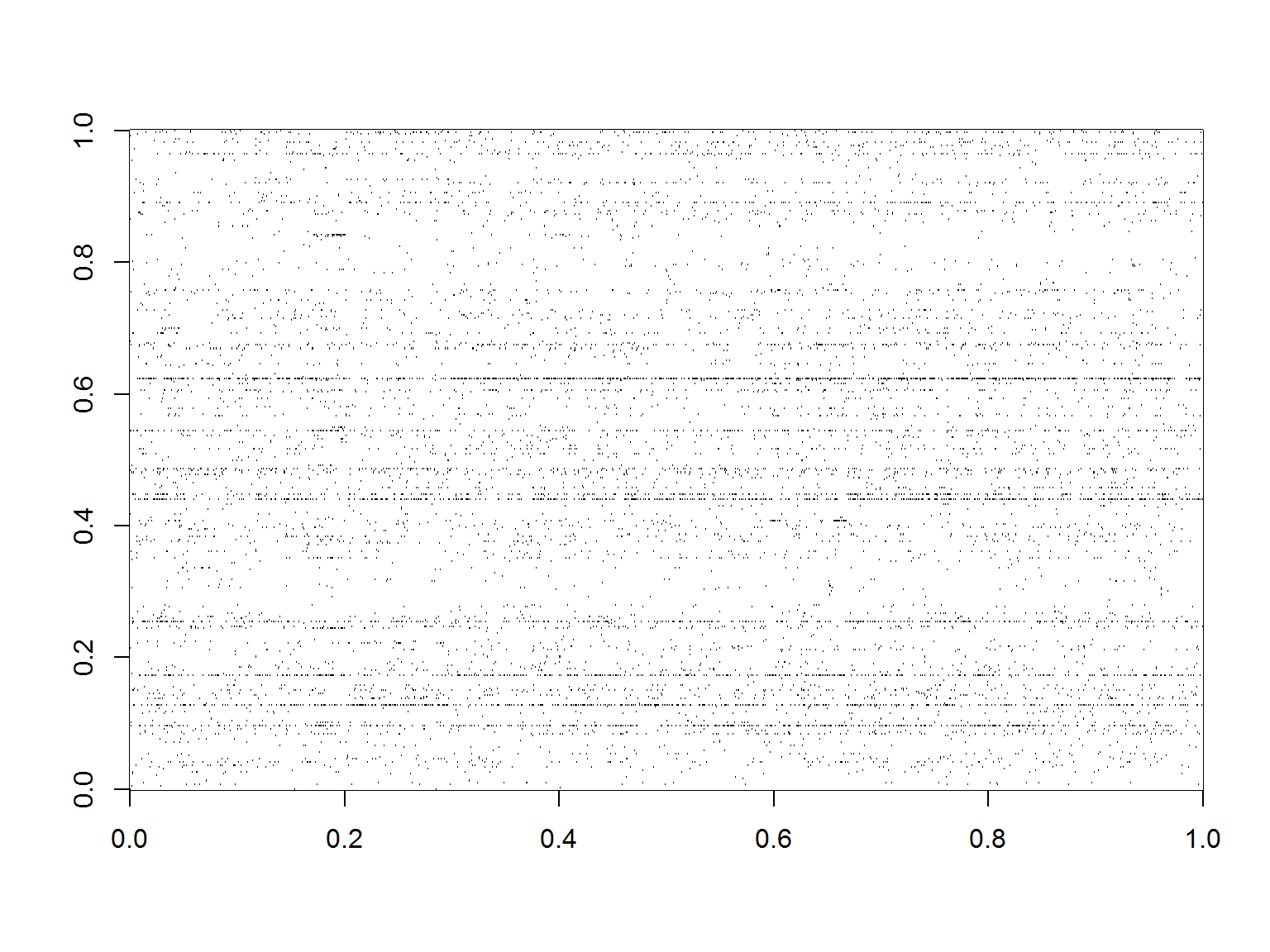
Mówiłem na początku, że to nieczytelne przy większych liczbach produktów i koszyków? No to teraz to widać. Widać też jedną wyróżniającą się linię poziomą, która biegnie przez prawie wszystkie koszyki. To oczywiście najpopularniejszy pieprz.
Przygotujmy zestaw reguł:
|
1 2 3 4 5 |
itemsets <- apriori(trans, parameter = list(supp=0.02, conf=0.2, target="rules", minlen=2)) # żeby nie było reguł z jednym elementem |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
## Apriori ## ## Parameter specification: ## confidence minval smax arem aval originalSupport maxtime support minlen ## 0.2 0.1 1 none FALSE TRUE 5 0.02 2 ## maxlen target ext ## 10 rules FALSE ## ## Algorithmic control: ## filter tree heap memopt load sort verbose ## 0.1 TRUE TRUE FALSE TRUE 2 TRUE ## ## Absolute minimum support count: 342 ## ## set item appearances ...[0 item(s)] done [0.00s]. ## set transactions ...[394 item(s), 17123 transaction(s)] done [0.01s]. ## sorting and recoding items ... [87 item(s)] done [0.00s]. ## creating transaction tree ... done [0.01s]. ## checking subsets of size 1 2 3 4 done [0.01s]. ## writing ... [378 rule(s)] done [0.00s]. ## creating S4 object ... done [0.00s]. |
|
1 |
summary(itemsets) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
## set of 378 rules ## ## rule length distribution (lhs + rhs):sizes ## 2 3 4 ## 174 164 40 ## ## Min. 1st Qu. Median Mean 3rd Qu. Max. ## 2.000 2.000 3.000 2.646 3.000 4.000 ## ## summary of quality measures: ## support confidence lift ## Min. :0.02003 Min. :0.2012 Min. :0.4505 ## 1st Qu.:0.02367 1st Qu.:0.3263 1st Qu.:1.4751 ## Median :0.02961 Median :0.4996 Median :1.7623 ## Mean :0.03935 Mean :0.4949 Mean :1.9082 ## 3rd Qu.:0.04427 3rd Qu.:0.6484 3rd Qu.:2.2421 ## Max. :0.19418 Max. :0.8436 Max. :6.0427 ## ## mining info: ## data ntransactions support confidence ## trans 17123 0.02 0.2 |
Mamy 378 reguł, zobaczmy po 20 z największymi kolejnymi wskaźnikami:
Największy support
|
1 |
inspect(head(sort(itemsets, by="support"), 20)) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
## lhs rhs support confidence lift ## [1] {cebula} => {pieprz} 0.19418326 0.7556818 1.6288444 ## [2] {pieprz} => {cebula} 0.19418326 0.4185549 1.6288444 ## [3] {czosnek} => {pieprz} 0.18203586 0.7177067 1.5469903 ## [4] {pieprz} => {czosnek} 0.18203586 0.3923716 1.5469903 ## [5] {masło} => {pieprz} 0.14197279 0.4388087 0.9458359 ## [6] {pieprz} => {masło} 0.14197279 0.3060171 0.9458359 ## [7] {cukier} => {masło} 0.12976698 0.4221927 1.3049107 ## [8] {masło} => {cukier} 0.12976698 0.4010830 1.3049107 ## [9] {jajko} => {masło} 0.12007242 0.5195855 1.6059320 ## [10] {masło} => {jajko} 0.12007242 0.3711191 1.6059320 ## [11] {czosnek} => {cebula} 0.11510833 0.4538338 1.7661353 ## [12] {cebula} => {czosnek} 0.11510833 0.4479545 1.7661353 ## [13] {mąka} => {masło} 0.10576418 0.6185109 1.9116900 ## [14] {masło} => {mąka} 0.10576418 0.3268953 1.9116900 ## [15] {jajko} => {cukier} 0.09811365 0.4245641 1.3813054 ## [16] {cukier} => {jajko} 0.09811365 0.3192096 1.3813054 ## [17] {olej} => {pieprz} 0.09642002 0.5708852 1.2305221 ## [18] {pieprz} => {olej} 0.09642002 0.2078298 1.2305221 ## [19] {jajko} => {pieprz} 0.09501840 0.4111701 0.8862620 ## [20] {pieprz} => {jajko} 0.09501840 0.2048087 0.8862620 |
Widzimy najpopularniejsze połączenia, które znamy już z wcześniejszej analizy.
Największy confidence
|
1 |
inspect(head(sort(itemsets, by="confidence"), 20)) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
## lhs rhs support confidence ## [1] {mąka,żółtka} => {masło} 0.02645564 0.8435754 ## [2] {majeranek} => {pieprz} 0.02125796 0.8406467 ## [3] {cebula,jajko} => {pieprz} 0.04426794 0.8375691 ## [4] {cebula,czosnek,masło} => {pieprz} 0.02324359 0.8343816 ## [5] {masło,tymianek} => {pieprz} 0.02020674 0.8297362 ## [6] {cebula,tymianek} => {pieprz} 0.02487882 0.8255814 ## [7] {cebula,mąka} => {pieprz} 0.03136133 0.8198473 ## [8] {cebula,natka pietruszki} => {pieprz} 0.02464521 0.8178295 ## [9] {jajko,masło,proszek do pieczenia} => {cukier} 0.02137476 0.8169643 ## [10] {cebula,masło} => {pieprz} 0.06114583 0.8078704 ## [11] {czosnek,śmietana} => {pieprz} 0.02353560 0.8027888 ## [12] {cukier,masło,proszek do pieczenia} => {jajko} 0.02137476 0.8026316 ## [13] {czosnek,tymianek} => {pieprz} 0.02598844 0.8003597 ## [14] {bulion,masło} => {pieprz} 0.02207557 0.7991543 ## [15] {seler} => {pieprz} 0.02137476 0.7991266 ## [16] {czosnek,masło} => {pieprz} 0.04572797 0.7989796 ## [17] {mleko,żółtka} => {cukier} 0.02125796 0.7930283 ## [18] {cebula,śmietana} => {pieprz} 0.03042691 0.7929985 ## [19] {czosnek,jajko} => {pieprz} 0.02814927 0.7927632 ## [20] {wanilia} => {cukier} 0.02184197 0.7857143 ## lift ## [1] 2.607318 ## [2] 1.811983 ## [3] 1.805349 ## [4] 1.798479 ## [5] 1.788466 ## [6] 1.779510 ## [7] 1.767151 ## [8] 1.762801 ## [9] 2.657967 ## [10] 1.741335 ## [11] 1.730382 ## [12] 3.473202 ## [13] 1.725146 ## [14] 1.722548 ## [15] 1.722488 ## [16] 1.722171 ## [17] 2.580092 ## [18] 1.709279 ## [19] 1.708772 ## [20] 2.556296 |
W 84% przepisów z mąką i żółtkiem potrzebne jest też masło. W 81% przypadków gdzie jest jajko, masło i proszek do pieczenia potrzebny jest cukier. To ciasta i desery. Swoją drogą co to za przepisy te pozostałe 9%?
Największy lift
|
1 |
inspect(head(sort(itemsets, by="lift"), 20)) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
## lhs rhs ## [1] {cukier,jajko,masło} => {proszek do pieczenia} ## [2] {cukier,jajko} => {proszek do pieczenia} ## [3] {proszek do pieczenia} => {mąka pszenna} ## [4] {mąka pszenna} => {proszek do pieczenia} ## [5] {drożdże} => {mleko} ## [6] {cukier,mąka} => {proszek do pieczenia} ## [7] {cukier,jajko,masło} => {mąka pszenna} ## [8] {jajko,masło} => {proszek do pieczenia} ## [9] {cukier,jajko} => {mąka pszenna} ## [10] {cukier,masło} => {proszek do pieczenia} ## [11] {cukier,mleko} => {żółtka} ## [12] {drożdże} => {mąka} ## [13] {bazylia} => {pomidory} ## [14] {pomidory} => {bazylia} ## [15] {cukier,żółtka} => {mleko} ## [16] {cukier,masło,proszek do pieczenia} => {jajko} ## [17] {masło,proszek do pieczenia} => {jajko} ## [18] {jajko,masło} => {mąka pszenna} ## [19] {cukier,proszek do pieczenia} => {jajko} ## [20] {cukier,masło} => {mąka pszenna} ## support confidence lift ## [1] 0.02137476 0.3236074 6.042672 ## [2] 0.03036851 0.3095238 5.779691 ## [3] 0.02061555 0.3849509 5.173873 ## [4] 0.02061555 0.2770801 5.173873 ## [5] 0.02108275 0.6087690 4.770687 ## [6] 0.02014834 0.2540501 4.743838 ## [7] 0.02149156 0.3253758 4.373163 ## [8] 0.02616364 0.2178988 4.068791 ## [9] 0.02902529 0.2958333 3.976102 ## [10] 0.02663085 0.2052205 3.832051 ## [11] 0.02125796 0.3082134 3.791335 ## [12] 0.02143316 0.6188870 3.619263 ## [13] 0.02306839 0.4131799 3.613320 ## [14] 0.02306839 0.2017365 3.613320 ## [15] 0.02125796 0.4510533 3.534730 ## [16] 0.02137476 0.8026316 3.473202 ## [17] 0.02616364 0.7671233 3.319548 ## [18] 0.02943409 0.2451362 3.294715 ## [19] 0.03036851 0.7591241 3.284933 ## [20] 0.03095252 0.2385239 3.205843 |
Widzimy, że jeśli w przepisie jest cukier, jajko i masło to bardzo prawdopodobne jest, że potrzebny będzie też proszek do pieczenia. Ma to sens.
Wśród reguł możemy sobie czegoś poszukać, na przykład:
tam gdzie potrzebne jest jajko potrzebne są też…
|
1 2 3 4 5 |
itemsets %>% subset(lhs %in% "jajko") %>% sort(by = "support") %>% head(20) %>% inspect() |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
## lhs rhs support confidence lift ## [1] {jajko} => {masło} 0.12007242 0.5195855 1.6059320 ## [2] {jajko} => {cukier} 0.09811365 0.4245641 1.3813054 ## [3] {jajko} => {pieprz} 0.09501840 0.4111701 0.8862620 ## [4] {jajko} => {mąka} 0.08923670 0.3861511 2.2582192 ## [5] {cukier,jajko} => {masło} 0.06605151 0.6732143 2.0807668 ## [6] {jajko,masło} => {cukier} 0.06605151 0.5500973 1.7897237 ## [7] {jajko} => {mleko} 0.05974420 0.2585292 2.0259933 ## [8] {jajko,mąka} => {masło} 0.05711616 0.6400524 1.9782701 ## [9] {jajko,masło} => {mąka} 0.05711616 0.4756809 2.7817912 ## [10] {jajko} => {cebula} 0.05285289 0.2287086 0.8900404 ## [11] {jajko} => {olej} 0.04899842 0.2120293 1.2553866 ## [12] {jajko,mąka} => {cukier} 0.04613678 0.5170157 1.6820939 ## [13] {cukier,jajko} => {mąka} 0.04613678 0.4702381 2.7499614 ## [14] {cebula,jajko} => {pieprz} 0.04426794 0.8375691 1.8053493 ## [15] {jajko,pieprz} => {cebula} 0.04426794 0.4658881 1.8130460 ## [16] {jajko,mleko} => {masło} 0.03977107 0.6656891 2.0575082 ## [17] {jajko,masło} => {mleko} 0.03977107 0.3312257 2.5956876 ## [18] {jajko,masło} => {pieprz} 0.03725983 0.3103113 0.6688646 ## [19] {jajko,pieprz} => {masło} 0.03725983 0.3921328 1.2120017 ## [20] {jajko,mleko} => {cukier} 0.03661742 0.6129032 1.9940608 |
do których składników potrzebny też cukier?
|
1 2 3 4 5 |
itemsets %>% subset(rhs %in% "cukier") %>% sort(by = "support") %>% head(20) %>% inspect() |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
## lhs rhs support confidence ## [1] {masło} => {cukier} 0.12976698 0.4010830 ## [2] {jajko} => {cukier} 0.09811365 0.4245641 ## [3] {mąka} => {cukier} 0.07930853 0.4637978 ## [4] {mleko} => {cukier} 0.06897156 0.5405034 ## [5] {jajko,masło} => {cukier} 0.06605151 0.5500973 ## [6] {masło,mąka} => {cukier} 0.05594814 0.5289895 ## [7] {woda} => {cukier} 0.05507213 0.4741076 ## [8] {żółtka} => {cukier} 0.04712959 0.5797414 ## [9] {jajko,mąka} => {cukier} 0.04613678 0.5170157 ## [10] {śmietana} => {cukier} 0.04561117 0.3426942 ## [11] {olej} => {cukier} 0.04374233 0.2589903 ## [12] {mąka pszenna} => {cukier} 0.04309992 0.5792779 ## [13] {masło,mleko} => {cukier} 0.04280792 0.5969055 ## [14] {cynamon} => {cukier} 0.04128949 0.6218118 ## [15] {proszek do pieczenia} => {cukier} 0.04000467 0.7470011 ## [16] {jajko,mleko} => {cukier} 0.03661742 0.6129032 ## [17] {jajko,masło,mąka} => {cukier} 0.03387257 0.5930470 ## [18] {masło,żółtka} => {cukier} 0.03141973 0.5971143 ## [19] {masło,mąka pszenna} => {cukier} 0.03095252 0.6487148 ## [20] {jajko,proszek do pieczenia} => {cukier} 0.03036851 0.7726597 ## lift ## [1] 1.3049107 ## [2] 1.3813054 ## [3] 1.5089512 ## [4] 1.7585104 ## [5] 1.7897237 ## [6] 1.7210502 ## [7] 1.5424937 ## [8] 1.8861698 ## [9] 1.6820939 ## [10] 1.1149444 ## [11] 0.8426166 ## [12] 1.8846618 ## [13] 1.9420128 ## [14] 2.0230445 ## [15] 2.4303438 ## [16] 1.9940608 ## [17] 1.9294593 ## [18] 1.9426921 ## [19] 2.1105726 ## [20] 2.5138234 |
Te dwa przykłady można przełożyć na normalne zakupy. Z czym kupowane są chipsy? A jak ktoś kupuje pieluchy to co kupuje jeszcze? W powyższych przykładach dane posortowane zostały po kolumnie support, ale na przykład planując promocje można oprzeć się na lift. O co chodzi?
Wiedząc, że zakup piwa bardzo często powiązany jest z zakupem chipsów (powinien być wysoki lift) możemy zrobić kilka rzeczy w samym sklepie:
- postawić obok siebie te produkty – bo jak już wziąłem piwo z półki to wezmę chipsy – tym bardziej, że są pod ręką
- przygotować ofertę kupując 6 piw chipsy gratis – bo często produkty te są kupowane razem, więc podnosząc ceną piwa możemy zrekompensować “stratę” na gratisowych chipsach. Oczywiście jak nie skorzystasz z promocji to owe 6 piw kosztuje nieco więcej
Dodatkowo mając pełne listy koszyków na przykład z całego tygodnia, godzina po godzinie, możemy przeanalizować schematy zakupów. Czy wieczorem kupowane jest coś innego? I czy w innych kombinacjach? Dodając dane o pogodzie wiemy jeszcze więcej. A dodając informacje o kliencie (na podstawie numeru karty kredytowej czy karty lojalnościowego) możemy wręcz prognozować co i kiedy kupi. I odpowiednio kierować do niego promocje i reklamy.
Pingback: Analiza tekstów z wiadomości | Łukasz Prokulski
Mały probelm przy generowaniu połączeń
skladniki_polaczenia %
select(n, skladniki) %>%
# podziel po numerze przepisu
slice_rows(„n”) %>%
# dla kazdej grupy macierz kazdy-kazdy
by_slice(~ dcast(., formula = skladniki ~ skladniki,
fun.aggregate = length, value.var = „skladniki”) %>%
# pivot macierzy
melt(id.vars = „skladniki”, value.name = „value”) %>%
# bez przeciątnej macierzy (bez sam ze sobą)
filter(skladniki != variable) %>%
mutate(value = 1),
.collate = „list”) %>%
# wynikowe mikrotabelki złącz w jedną dużą
bind_rows(.$.out) %>%
select(skladniki, variable, value) %>%
filter(!is.na(value))
# posumuj pary składników
skladniki_polaczenia %
mutate(prod_a = ifelse(skladniki < variable, skladniki, variable),
prod_b = ifelse(skladniki %
select(prod_a, prod_b, n = value) %>%
group_by(prod_a, prod_b) %>%
summarise(n = sum(n)) %>%
ungroup() %>%
distinct()
Error in skladniki_polaczenia %>% mutate(prod_a = ifelse(skladniki %”
A ten błąd to?… Bo to co najbardziej istotne nie pojawił się w Twoim komentarzu
np.
Error in trans@data %>% t() %>% data.matrix() %>% as.data.frame() %>% :
could not find function „%>%”
Okej zainstalowałam jeszcze kilka paczek i poszło ;)
Hej, jeszcze szukasz wyciagu z kasy fiskalnej?
https://archive.ics.uci.edu/ml/datasets/Online+Retail
pzdr