Dzisiaj trochę nadrabiana statystyki za pomogą R. Zobaczymy jak przetestować czy rozkład jest normalny, jak przetestować hipotezy i jak zbudować prosty model.
|
1 2 3 4 |
library(tidyverse) library(broom) library(knitr) library(kableExtra) |
Za dane przykładowe posłużą nam dane o wzroście i wadze w podziale na płeć. Wczytujemy dane – użyjemy zestawu danych z Kaggle (ściągnąłem je wcześniej na dysk):
|
1 2 3 4 5 6 7 8 9 10 |
data <- read_csv("weight-height.csv") # szybki rzut oka w dane glimpse(data) ## Observations: 10,000 ## Variables: 3 ## $ Gender <chr> "Male", "Male", "Male", "Male", "Male", "Male", "Male", "… ## $ Height <dbl> 73.84702, 68.78190, 74.11011, 71.73098, 69.88180, 67.2530… ## $ Weight <dbl> 241.8936, 162.3105, 212.7409, 220.0425, 206.3498, 152.212… |
Dziwne te liczby: wzrost w okolicach 70? Waga blisko 200? Dane są amerykańskie, więc wzrost mamy w calach, a wagę w funtach. Nie musimy, ale możemy przeliczyć to na jednostki metryczne – będzie nam łatwiej interpretować wyniki.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
data <- data %>% mutate(Height = Height * 2.54, # 1 cal = 2.54 cm Weight = Weight * 0.45359237) # 1 funt to 0.45 kg # znowu patrzymy w dane glimpse(data) ## Observations: 10,000 ## Variables: 3 ## $ Gender <chr> "Male", "Male", "Male", "Male", "Male", "Male", "Male", "… ## $ Height <dbl> 187.5714, 174.7060, 188.2397, 182.1967, 177.4998, 170.822… ## $ Weight <dbl> 109.72107, 73.62279, 96.49763, 99.80959, 93.59870, 69.042… |
Teraz wygląda to normlanie. Zobaczmy kilka rozkładów, od razu w podziale na płeć.
Zaleźność wagi od wzrostu:
|
1 2 3 4 |
ggplot(data) + geom_point(aes(Height, Weight, color = Gender), size = 0.1, alpha = 0.25) + scale_color_manual(values = c("Male" = "blue", "Female" = "red")) |
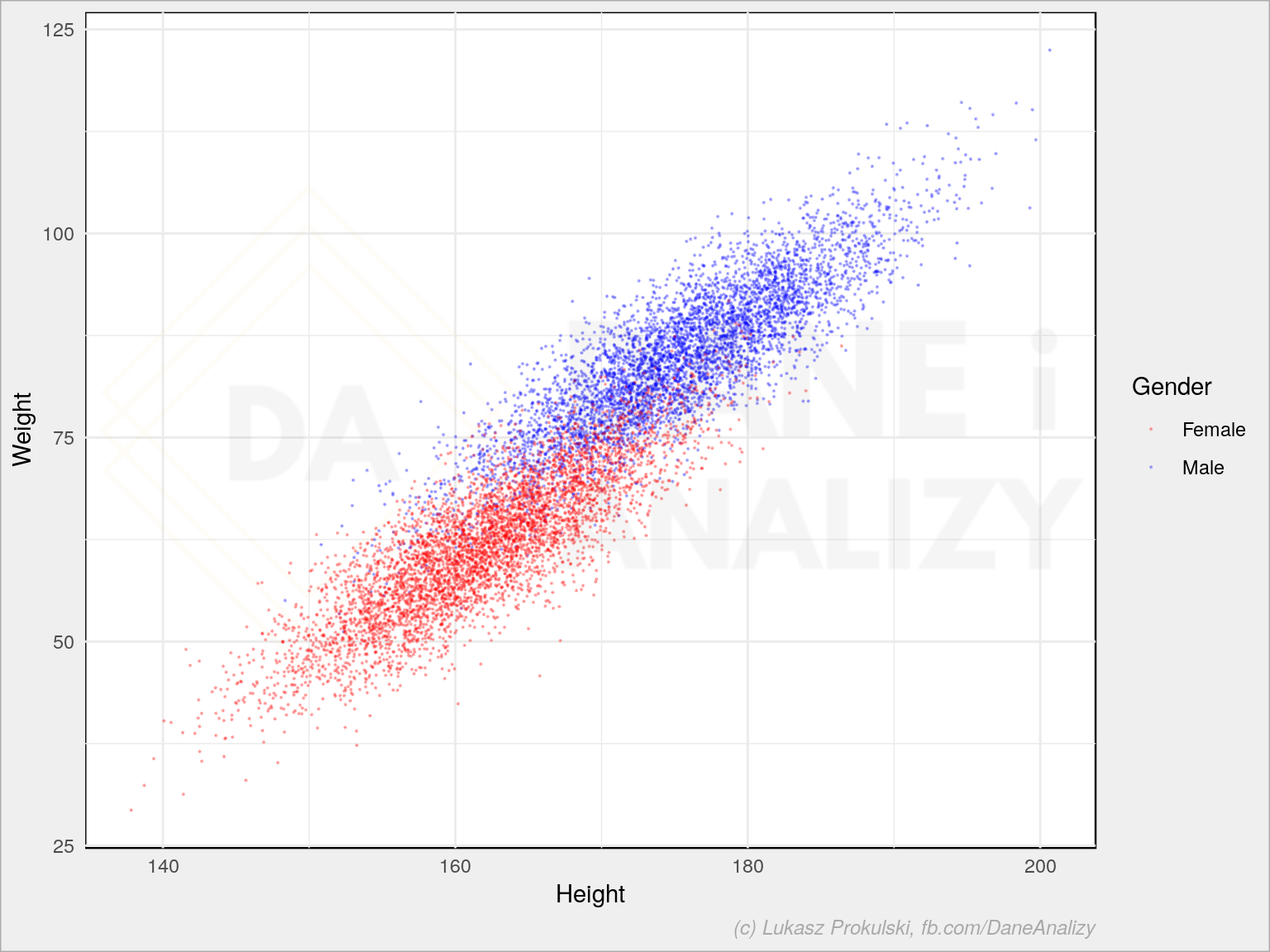
Rozkład wagi:
|
1 2 3 |
ggplot(data) + geom_density(aes(Weight, fill = Gender), alpha = 0.5) + scale_fill_manual(values = c("Male" = "blue", "Female" = "red")) |
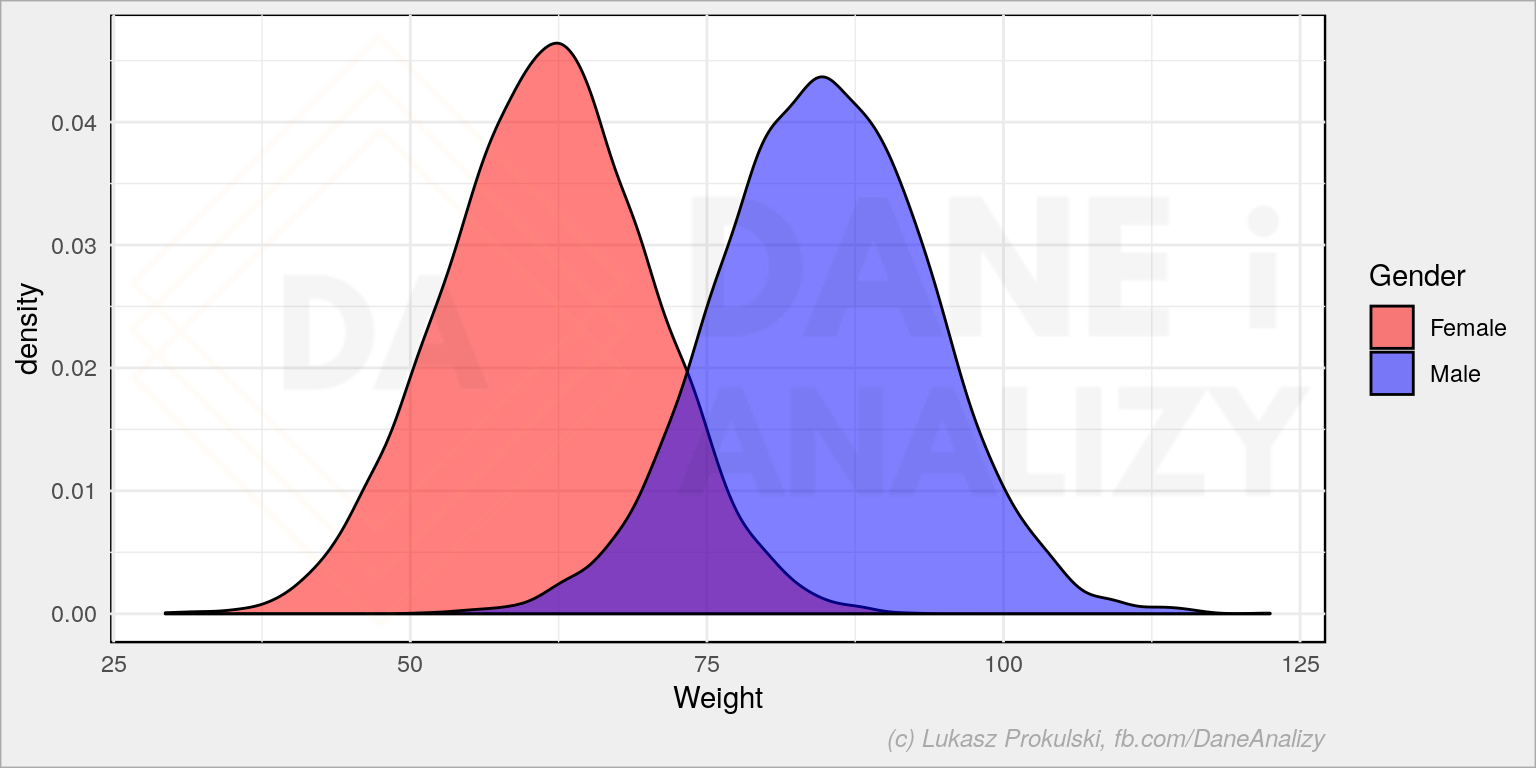
Rozkład wzrostu:
|
1 2 3 |
ggplot(data) + geom_density(aes(Height, fill = Gender), alpha = 0.5) + scale_fill_manual(values = c("Male" = "blue", "Female" = "red")) |
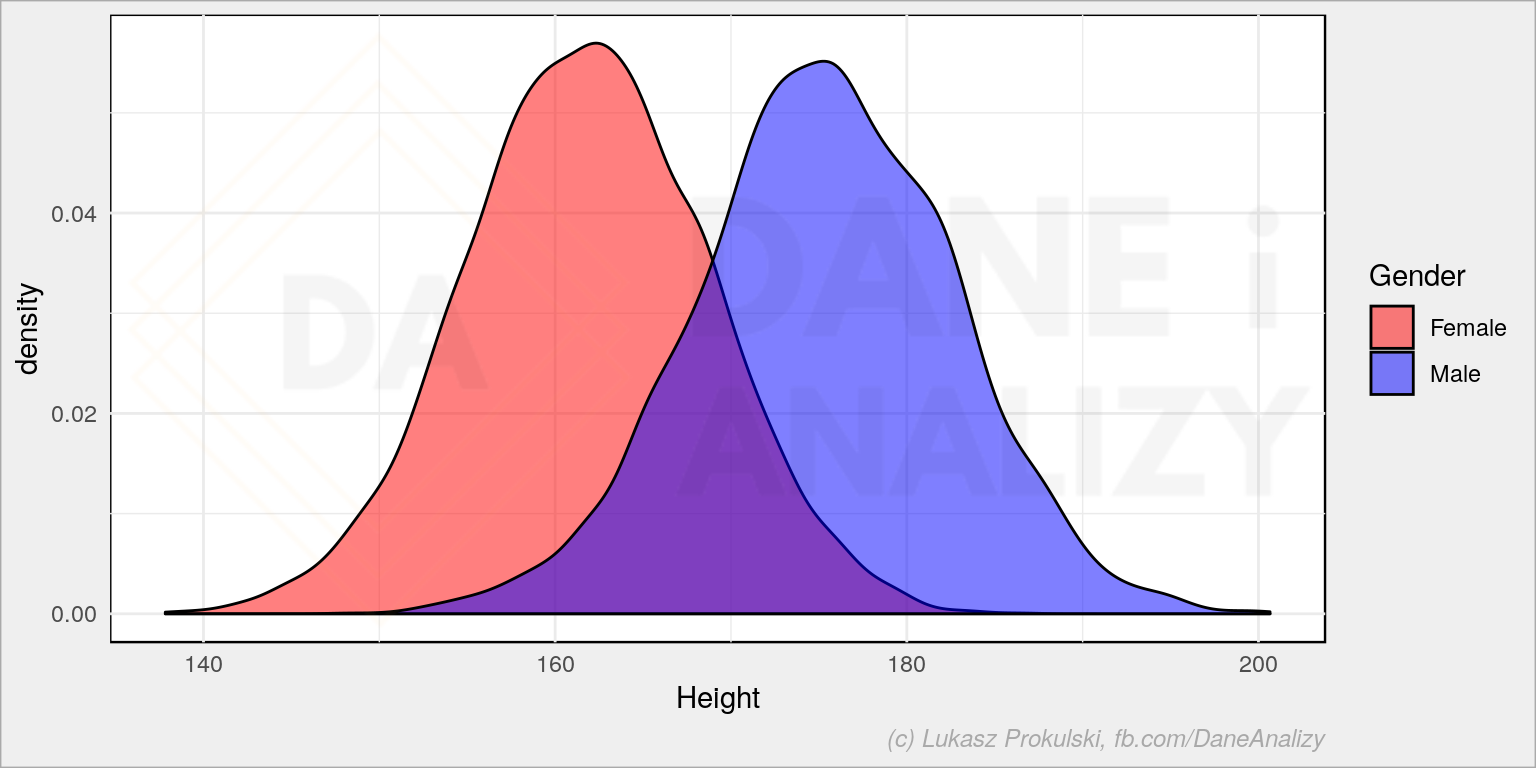
Zobaczmy teraz jakie właściwości mają te rozkłady. Jaka jest średnia, jakie są kwartyle, jakie jest odchylenie standardowe
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
# obliczmy statystyki opisowe dla wzrostu stats_Height <- data %>% select(Gender, Height) %>% # budujemy zagnieżdzone DF per płeć nest(-Gender) %>% # liczymy statystyki opisowe dla obu parametrów w zagnieżdzonych tabelkach mutate(stats = map(data, ~map_dfc(lst(min, mean, median, max, sd), function(.fun) .fun(.x$Height)))) %>% # nie potrzebujemy danych select(-data) %>% # rozgnieżdzamy tabele unnest() %>% mutate(Feature = "Height") %>% gather("Param", "Value", -Feature, -Gender) %>% spread(Gender, Value) # to samo robimy dla wagi stats_Weight <- data %>% select(Gender, Weight) %>% nest(-Gender) %>% mutate(stats = map(data, ~map_dfc(lst(min, mean, median, max, sd), function(.fun) .fun(.x$Weight)))) %>% select(-data) %>% unnest() %>% mutate(Feature = "Weight") %>% gather("Param", "Value", -Feature, -Gender) %>% spread(Gender, Value) # łączymy obie tabele stats <- bind_rows(stats_Weight, stats_Height) %>% # cechy zmieniamy na faktory i ustalamy ich kolejność (do sortowania) mutate(Param = factor(Param, levels = c("min", "mean", "median", "max", "sd"), labels = c("Minimum", "Mean", "Median", "Maximum", "Std. dev."))) %>% # sortujemy tabelkę w odpowiedni sposób arrange(Feature, Param) # tabelka: stats %>% # to co jest kolumną liczbową zaokrąglamy do 1 miejsca po przecinku mutate_if(is.numeric, ~ round(.x, 1)) %>% kable(format = "html") %>% kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive")) |
| Feature | Param | Female | Male |
|---|---|---|---|
| Height | Minimum | 137.8 | 148.4 |
| Height | Mean | 161.8 | 175.3 |
| Height | Median | 161.9 | 175.3 |
| Height | Maximum | 186.4 | 200.7 |
| Height | Std. dev. | 6.8 | 7.3 |
| Weight | Minimum | 29.3 | 51.2 |
| Weight | Mean | 61.6 | 84.8 |
| Weight | Median | 61.7 | 84.8 |
| Weight | Maximum | 91.7 | 122.5 |
| Weight | Std. dev. | 8.6 | 9.0 |
Ciekawe nie ma wiekich ciekawostek, ale warto zwrócić uwagę na dwie liczby, które za chwilę będziemy porównywać (nie wprost) – średni wzrost kobiet to około 162 cm, a mężczyzn – 175 cm.
Test normalności
Widać to co prawda od razu, ale sprawdźmy czy rozkład wzrostu i wagi jest rozkładem normalnym. Przy zastosowaniu wielu metod statystycznych ważne jest, aby zbiór był zbiorem podlegającym rozkładowi normalnemu. Szczegóły w podręcznikach ;)
Hipotezy zerowa oraz alternatywna są następującej postaci:
- H0: Rozkład badanej cechy jest rozkładem normalnym.
- H1: Rozkład badanej cechy nie jest rozkładem normalnym.
Test Shapiro-Wilka
To jeden z najbardziej popularnych testów i najczęściej wykorzystywanych. Funkcja shapiro.test() z pakietu stats (wbudowany w R, nie trzeba go instalować) pozwala na przetestowania od 3 do 5000 próbek. Na szczęście mamy po 5000 pomiarów dla każdej z płci.
|
1 2 3 4 5 6 7 8 |
data %>% group_by(Gender) %>% summarise(shapiro_Height = shapiro.test(Height)$p.value, shapiro_Weight = shapiro.test(Weight)$p.value) %>% ungroup() %>% mutate_if(is.numeric, ~ round(.x, 4)) %>% kable(format = "html") %>% kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive")) |
| Gender | shapiro_Height | shapiro_Weight |
|---|---|---|
| Female | 0.9022 | 0.9134 |
| Male | 0.1402 | 0.3828 |
Za chwilę omówimy wyniki, ale prosta znajomość zasad testowania hipotez już pozwala rozpoznać odpowiedź.
Test Kołmogorowa-Smirnowa
Drugi test jest również często spotykany, nad testem Shapiro-Wilka ma tą przewagę, że pozwala porównać dwa rozkłady (czyli sprawdzić czy dana próbka ma rozkład jaki znamy). Tutaj jednak wcześniej potrzebne jest skalowanie zmiennych, bez którego wartość zwracana w $p.value funkcji ks.test() jest równa zero (mimo że wynik wyświetlany na ekranie jest taki sam).
|
1 2 3 4 5 6 7 8 |
data %>% group_by(Gender) %>% summarise(ks_Height = ks.test(scale(Height), "pnorm")$p.value, ks_Weight = ks.test(scale(Weight), "pnorm")$p.value) %>% ungroup() %>% mutate_if(is.numeric, ~ round(.x, 4)) %>% kable(format = "html") %>% kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive")) |
| Gender | ks_Height | ks_Weight |
|---|---|---|
| Female | 0.9127 | 0.9525 |
| Male | 0.6088 | 0.9834 |
We wszystkich przypadkach (dla każdej płci, obu cech i w obu testach) wartość p-value jest większa od naszego (standardowo zakładanego) przedziału ufności 0.05, zatem nie możemy odrzucić hipotezy H0, czyli – mamy do czynienia z rozkładami normalnymi.
Więcej (z opisem i matematyką za nimi stojącą) o testach na normalność rozkładu znajdziecie na blogu SmarterPoland.pl.
Czy mężczyźni są wyżsi od kobiet?
To wiemy z doświadczenia, z powyższych wykresów z rozkładem oraz tabelki z podstawowymi liczbami opisującymi statystykę: średnie wzrostu są różne. Ale jak to zbadać w R? Użyjemy testu t-Studenta. Hipotezy tym razem wyglądają następująco:
- H0: kobiety i mężczyźni są średnio tego samego wzrostu
- H1: średni wzrost różni się pomiędzy płciami
Do testu użyjemy funkcji t.test():
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
t.test(data %>% filter(Gender == "Male") %>% pull(Height), # wzrost mężczyzn data %>% filter(Gender == "Female") %>% pull(Height)) # wzrost kobiet ## ## Welch Two Sample t-test ## ## data: data %>% filter(Gender == "Male") %>% pull(Height) and data %>% filter(Gender == "Female") %>% pull(Height) ## t = 95.603, df = 9962.1, p-value < 2.2e-16 ## alternative hypothesis: true difference in means is not equal to 0 ## 95 percent confidence interval: ## 13.22970 13.78357 ## sample estimates: ## mean of x mean of y ## 175.3269 161.8203 |
p-value jest dużo mniejsze od 0.05, zatem na 95% możemy odrzucić H0 i przyznać, że średni wzrost różni się między płciami.
Ale czy kobiety są wyższe czy niższe? Ponownie użyjemy tego samego testu z jednym dodatkowym parametrem alternative. Tutaj hipotezy mamy następujące:
- H0: mężczyźni są wyższi od kobiet
- H1: mężczyźni nie są wyżsi od kobiet
Zatem porównujemy czy pierwszy zbiór (wzrost mężczyzn) ma średnią większą od średniej drugiego zbioru (wzrost kobiet):
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
t.test(data %>% filter(Gender == "Male") %>% pull(Height), # wzrost mężczyzn data %>% filter(Gender == "Female") %>% pull(Height), # wzrost kobiet alternative = "greater") # pierwsza średnia większa od drugiej średniej ## ## Welch Two Sample t-test ## ## data: data %>% filter(Gender == "Male") %>% pull(Height) and data %>% filter(Gender == "Female") %>% pull(Height) ## t = 95.603, df = 9962.1, p-value < 2.2e-16 ## alternative hypothesis: true difference in means is greater than 0 ## 95 percent confidence interval: ## 13.27423 Inf ## sample estimates: ## mean of x mean of y ## 175.3269 161.8203 |
p-value < 0.05 więc na 95% nie możemy odrzucić H0 co oznacza, że średnio mężczyźni są wyżsi od kobiet.
Model – regresja logistyczna
Czy na podstawie wzrostu i wagi możemy określić płeć? Spróbujmy zbudować stosowny, prosty, model.
Do wyboru mamy wynik będący jedną z dwóch płci, zatem zastosujemy regresję logistyczną.
W pierwszym kroku jednak podzielmy dane na uczące train i testowe test na których zbadany dokładność działania modelu.
|
1 2 3 4 5 6 |
# losujemu 80% wierszy - ich ID ids <- sample(1:nrow(data), 0.80*nrow(data)) # dane treningowe: train <- data[ids, ] # pozostałe dane będą testem: test <- data[-ids, ] |
Teraz zbudujemy prosty model. Odpowiedź musi być factorem:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
model_glm <- glm(as.factor(Gender) ~ Weight + Height, data = train, family = "binomial") model_glm ## ## Call: glm(formula = as.factor(Gender) ~ Weight + Height, family = "binomial", ## data = train) ## ## Coefficients: ## (Intercept) Weight Height ## 1.2985 0.4394 -0.1986 ## ## Degrees of Freedom: 7999 Total (i.e. Null); 7997 Residual ## Null Deviance: 11090 ## Residual Deviance: 3373 AIC: 3379 |
Mając model możemy dokonać predykcji na danych testowych:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# predykcja test$pred <- predict(model_glm, newdata = test) # jeśli wynik predykcji jest mniejszy od zera to płeć będzie pierwszym faktorem # (a liczą się one zgodnie z alfabetem, bo nie zmieniliśmy tego) test$pred_Gender <- if_else(test$pred < 0, "Female", "Male") # zobaczmy rozkład odpowiedzi modelu na dane testowe ggplot(test) + geom_violin(aes(Gender, pred, fill = Gender)) + scale_fill_manual(values = c("Male" = "blue", "Female" = "red")) |
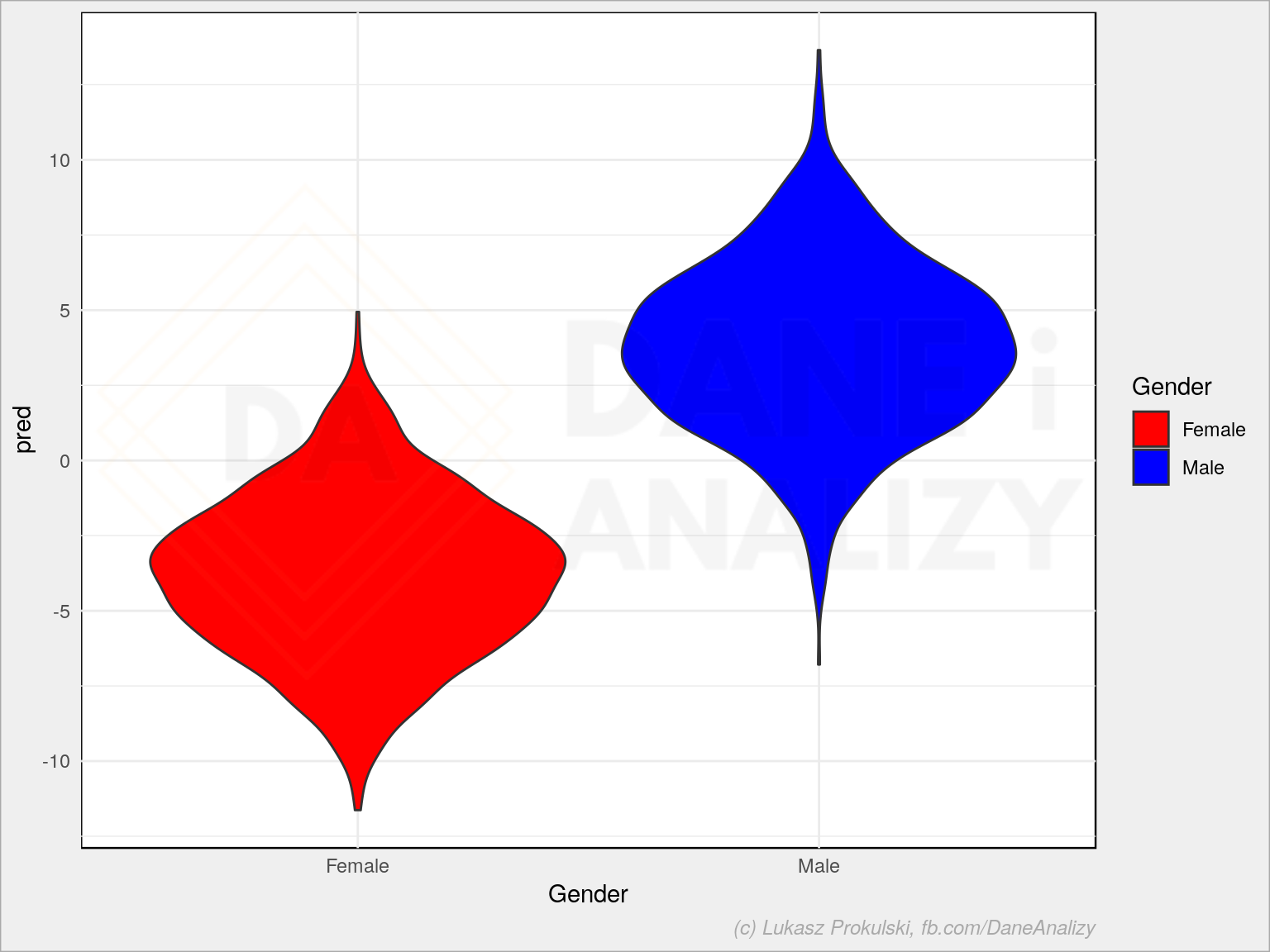
Sprwadźmy wynik:
|
1 2 3 4 5 6 |
table(test$Gender, test$pred_Gender) ## ## Female Male ## Female 912 72 ## Male 84 932 |
I skuteczność dopasowania:
|
1 2 3 |
sum(diag(table(test$Gender, test$pred_Gender))) / sum(table(test$Gender, test$pred_Gender)) ## [1] 0.922 |
W 92.2 procentach model przewidział trafnie wynik.
Model – las losowy
Spróbujmy z innym modelem – na przykład z lasem losowym.
|
1 2 3 4 5 6 7 8 9 |
library(randomForest) # budujemy model oparty na 100 drzewach model_rf <- randomForest(as.factor(Gender) ~ Weight + Height, data = train, ntree = 100) # przewidujemy wyniki test$pred_Gender_rf <- predict(model_rf, newdata = test) |
Wynik:
|
1 2 3 4 5 6 |
table(test$Gender, test$pred_Gender_rf) ## ## Female Male ## Female 906 78 ## Male 100 916 |
W tym przypadku poprawdność przewidywań to 91.1 procent, a zatem gorzej niż regresja logistyczna.
Nie zawsze więc wielki kombajn (jakim są lasy losowe) jest nam potrzebny.
Panie Łukaszu,
niepoprawnie odczytuje Pan wyniki testów statystycznych.
1. Przy testach na normalność rozkładu „zatem nie możemy odrzucić hipotezy alternatywnej H1” – nie jest to prawda. W tamtym wypadku „nie możemy odrzucić hipotezy zerowej H0”
2. Ma Pan również złe założenia przy teście t studenta z „greater = TRUE”. Tutaj hipoteza zerowa zostaje ta sama, zmienia się tylko hipoteza alternatywna (jedno większe niż drugie).
3. Nie można „pozostać przy” H0 (co najwyżej można jej nie odrzucić)
Pozdrawiam,
DK
Dzięki za komentarz. W 1. i 3. to faktycznie prawda – poprawiłem w tekście.
Co do 2 – nie bardzo rozumiem? Jak powinny zatem wyglądać te hipotezy?
(tak, ze statystyki zawsze byłem cieniasem ;))
> Ad2. Powinno to wyglądać mniej więcej tak:
H0: kobiety i mężczyźni są średnio tego samego wzrostu
H1: mężczyźni są średnio wyżsi od kobiet
> „p-value < 0.05 więc na 95% nie możemy odrzucić H0 co oznacza, że średnio mężczyźni są wyżsi od kobiet."
Zamiast tego można (powinno się) napisać "p-value Nie powinno się też mówić, że na „95%” odrzucamy coś. (Co to znaczy!?).
Ucięło mi część komentarza:
– „p-value < 0.05 więc na 95% nie możemy odrzucić H0 co oznacza, że średnio mężczyźni są wyżsi od kobiet."
Zamiast tego można (powinno się) napisać "p-value < 0.05 więc odrzucamy H0 i przyjmujemy HA co oznacza, że średnio mężczyźni są wyżsi od kobiet."
– Nie powinno się też mówić, że na „95%” odrzucamy coś. (Co to znaczy!?)
Witam,
Zgadzam się całkowicie z dk, zawsze odrzucamy H0 na korzyść HA, gdy p-value < 0.05. Warto jeszcze dodać, że w H0 w zasadzie zawsze mamy znak równości i nie możemy zakładać czegoś innego.
Natomiast taka rzecz jeszcze przyszła mi do głowy: skoro porównujemy dwie tylko grupy i test t-Studenta wykazał między nimi różnice statystycznie istotne, to nie potrzebujemy już dodatkowego testowania typu „która płeć jest tą wyższą”. Skoro są tylko dwie i się różnią, to wystarczy spojrzeć na średnie arytmetyczne i już to wiemy. Oczywiście dla udzielenia szczegółowej odpowiedzi profesjonalnej jest mieć HA jednostronną, czyli „większe” lub „mniejsze” niż dwustronną, czyli „różne”.