Tym razem przygotujemy środowisko do pracy z Keras i rozpoznamy kilka liczb (ponownie jak poprzednio).
Instalacja Keras
Zaczniemy od instalacji. Potrzebujemy zainstalowanego Pythona na maszynie. W unixach (w tym odcinku korzystam z serwera EC2 w AWS) nie jest to problem, pod Windowsem można zainstalować go na przykład instalując Anacondę.
Kolejny krok to przygotowanie R do pracy z Keras. Najpierw instalujemy bibliotekę keras:
|
1 |
install.packages("keras") |
a następnie sam silnik:
|
1 2 |
library(keras) install_keras() |
Ta ostatnia funkcja ma trochę parametrów – między innymi odpowiedzialnych z zainstalowanie TensorFlow skompilowanego pod korzystanie z GPU (wykorzystanie kart graficznych do obliczeń – znacznie przyspiesza to cały proces, ale potrzebny jest stosowny sprzęt). Odpowiedni ich opis znajdziecie w dokumentacji. Szczegółową dokumentację Keras znajdziecie na stronie Keras.io.
Proces instalacji nieco trwa za pierwszym razem, później jest już z górki. Przy instalacji na Windowsie może się coś pogryźć w Anacondzie (mi powstało drugie środowisko i trochę z tym trzeba powalczyć). Na maszynie EC2 (szczególnie t2.micro) może być okazać, że zabraknie pamięci (tak się stało dla sieci opisywanych poniżej). Rozwiązaniem jest zwiększenie wielkości tzw. swapu czyli wirtualnej pamięci, która tak na prawdę jest miejscem na dysku. Znalazłem odpowiednie obejście na niezastąpionym Stackoverflow. Stosujemy więc zwiększenie swapu, po resecie maszyny wszystko wraca do normy (chyba, że potrzebujemy pozostać przy powiększonym miejscu – odpowiednia zmiana opisana jest też na SO).
Przygotowanie danych
Pierwszy krok to przygotowanie danych – podobnie jak poprzednio wykorzystamy pliki CSV z Kaggle.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
library(keras) library(tidyverse) library(gridExtra) # parametry trenowania sieci VERBOSE = 1 EPOCHS = 15 BATCH_SIZE = 128 # ścieżki do plikow z danymi train_data_path <- "data/train.csv" test_data_path <- "data/test.csv" # wczytujemy dane treningowe train <- read_csv(train_data_path) |
Mamy dane. Dla każdego wiersza danych pierwsza kolumna opisuje nam co widzimy w danych zapisanych w kolejnych 784 kolumnach. Widzimy liczbę od 0 do 9. Keras potrzebuje tej informacji w formie binarnej macierzy: każdy wiersz to jedna liczba (ta z obrazka), a w odpowiedniej kolumnie mamy 1 jeśli to właśnie ta liczba lub zero jeśli to nie ona. Czyli dla czwórki w kolumnie 5 (liczymy od 0) będzie 1, a w pozostałych zera – widać to w czwartym wierszu poniższej tabeli. To one-hot-encoding – rozsmarowanie cech kategorycznych (czyli takich, które można wylistować czy też zesłownikować) na kolumny i umieszczenie w odpowiednich kolumnach jedynki.
Spójrzmy zresztą na wynik:
|
1 2 3 |
y_train <- to_categorical(train$label) head(y_train) |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Pozostałe dane to cechy (784 punktów dla każdej ręcznie pisanej liczby). Przekształcamy data frame jaki mamy z wczytania CSV na macierz (Keras/TensorFlow operuje na macierzach; właściwie cały deep learning to operacje na macierzach).
|
1 |
x_train <- train[, -1] %>% as.matrix() |
Mamy więc macierz odpowiedzi (10 kolumn z 1 lub 0 w 42000 wierszach – tyle ile liczb w zbiorze treningowym) oraz 784 cech (macierz 28×28 pikseli rozciągniętych na wektor).
Tutaj ważna sprawa: podobnie jak poprzednio dane opisujące liczbę traktujemy jako wektor czyli ciąg 784 wartości, a nie jak obrazek (macierz). To ważne założenie i ma wpływ na sposób budowania sieci neuronowych. W kolejnym odcinku obraz potraktujemy już jak obraz.
Zbudujemy pierwszy model – 10 neuronów w jednej warstwie. W poprzednim odcinku dla pełnych danych z użyciem sieci zbudowanej przy pomocy pakietu nnet udało się uzyskać dokładność rozpoznania liczb na poziomie 63.4% – to będzie nasz punkt odniesienia.
Model 1
Jak wygląda budowanie modelu w Keras? Bardzo prosto (a operator %>% pipe jeszcze bardziej to upraszcza). Pierwszy element to rodzaj modelu – w naszym przypadku będzie to model sekwencyjny (jedna warstwa za drugą). Do takiej informacji dodajemy kolejne warstwy.
W pierwszej warstwie musimy określić rozmiar danych wejściowych (długość wektora, wielkość macierzy i liczbę jej wymiarów itd), w ostatniej – liczbę wyjść. Tutaj mamy 10 wyjść, bo tyle mamy klas.
Po zbudowaniu architektury musimy ją skompilować (czyli wysłać do Kerasa w Pythonie, bo wszystko dzieje się tak na prawdę w Pythonie, R jest tutaj opakowaniem).
|
1 2 3 4 5 6 7 8 9 10 11 |
model <- keras_model_sequential() %>% # architektura sieci layer_dense(units = 10, activation = 'softmax', input_shape = c(784)) %>% # kompilacja modelu: compile( loss = 'categorical_crossentropy', optimizer = optimizer_rmsprop(), metrics = c('accuracy') ) summary(model) |
|
1 2 3 4 5 6 7 8 9 |
## ___________________________________________________________________________ ## Layer (type) Output Shape Param # ## =========================================================================== ## dense_1 (Dense) (None, 10) 7850 ## =========================================================================== ## Total params: 7,850 ## Trainable params: 7,850 ## Non-trainable params: 0 ## ___________________________________________________________________________ |
Widzimy, że nasz prosty model składa się z jednej warstwy w której powstaje 7850 parametrów. Dlaczego tyle? Mamy 10 neuronów i 784 cechy. To już po przemnożeniu daje 7840, gdzie brakujące 10? To wolne parametry, niezwiązane z wejściem (bias) dla każdej z klas.
Mając architekturę – czas na wytrenowanie modelu. To właśnie tutaj dzieją się obliczenia polegające na znalezieniu odpowiednich parametrów:
|
1 2 3 4 5 6 7 8 9 10 11 |
history <- model %>% fit( x_train, y_train, batch_size = BATCH_SIZE, epochs = EPOCHS, verbose = VERBOSE, validation_split = 0.2 ) plot(history) |
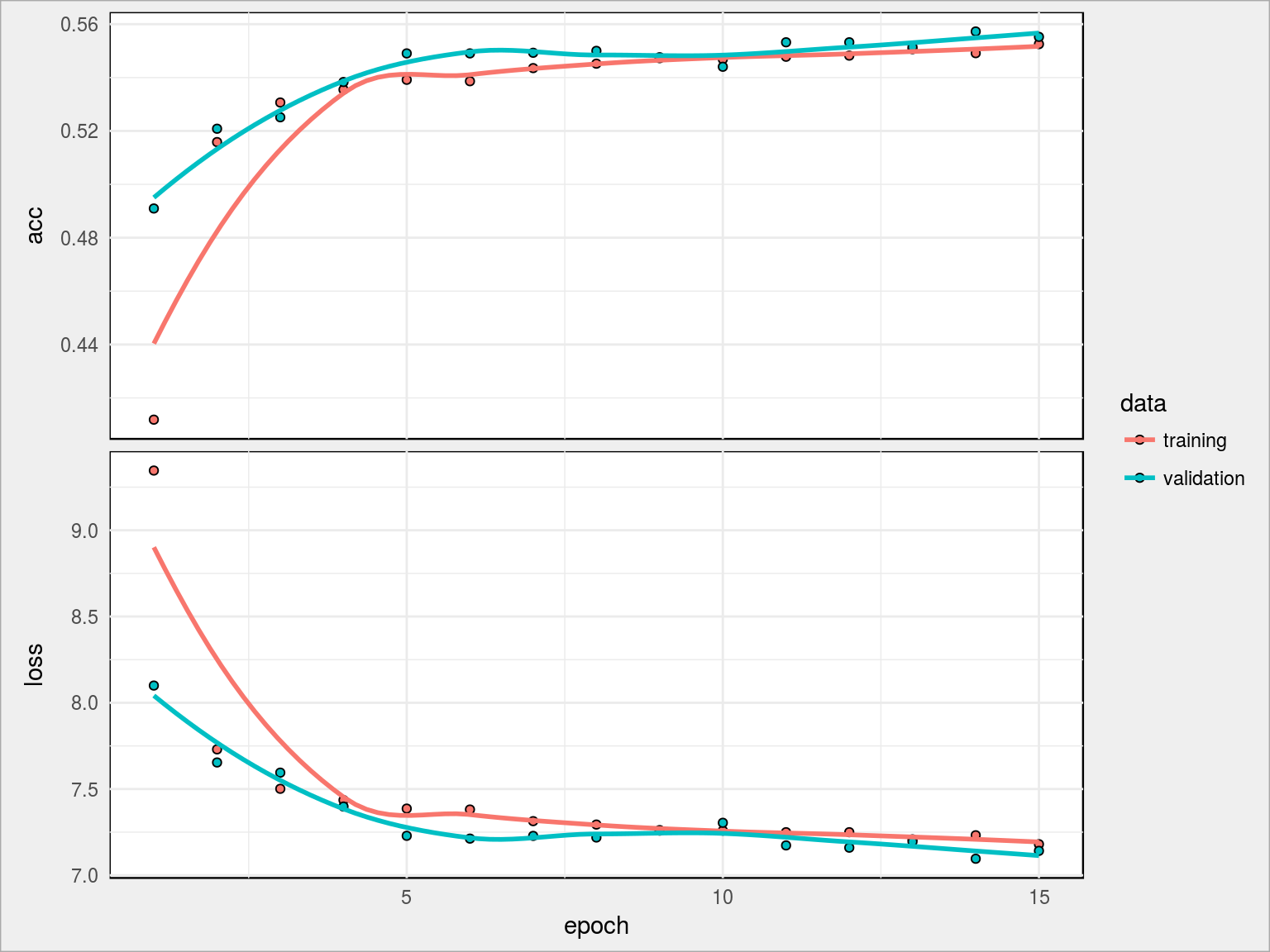
Wykresy obrazują uzyskane współczynniki określające jakość modelu w kolejnych krokach epoch. Co oznaczają te współczynniki?
- loss – błąd uczenia sieci, im mniejszy tym lepiej
- acc – poprawność modelu w przypisaniu klas na danych treningowych
- val_loss oraz val_acc są analogiczne do powyższych, z tą zasadniczą różnicą, że val_ to miara na części sprawdzającej danych treningowych, czyli tej która nie była wykorzystana do uczenia (Keras sam sobie to dzieli, nie musimy robić tego wprost).
Której miary użyć? Jeżeli chcemy sprawdzić poprawność działania modelu na nowych danych (po to robi się modele: uczymy na czymś co znamy, a nieznane wrzucamy do modelu i oczekujemy wyników) powinniśmy patrzyć na wartość val_acc.
Po co zatem acc i val_acc? Ano po to, ze w sytuacji kiedy acc rośnie, a val_acc maleje mamy do czynienia z overfittingiem czyli nadmiernym dopasowaniem modelu do danych, co w dużym uproszczeniu można wytłumaczyć tym że sieć zapamiętuje odpowiedzi a nie uczy się.
W powyższym modelu widzimy, że po 10 epochach wyniki stabilizują się i acc podąża mniej więcej równo z val_acc. Otrzymany wynik to 55.52% dokładności rozpoznania liczby co już zachęca do dalszych działań (to ponad 10 punktów procentowych lepiej niż wynik otrzymany z użyciem nnet).
Model 2
W drugim modelu dodamy jedną warstwę z 5 neuronami. Ścieżka jest taka sama, zatem:
Architektura sieci:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
model <- keras_model_sequential() %>% # architektura sieci: layer_dense(units = 5, activation = 'relu', input_shape = c(784)) %>% layer_dense(units = 10, activation = 'softmax') %>% # kompilacja modelu: compile( loss = 'categorical_crossentropy', optimizer = optimizer_rmsprop(), metrics = c('accuracy') ) summary(model) |
|
1 2 3 4 5 6 7 8 9 10 11 |
## ___________________________________________________________________________ ## Layer (type) Output Shape Param # ## =========================================================================== ## dense_2 (Dense) (None, 5) 3925 ## ___________________________________________________________________________ ## dense_3 (Dense) (None, 10) 60 ## =========================================================================== ## Total params: 3,985 ## Trainable params: 3,985 ## Non-trainable params: 0 ## ___________________________________________________________________________ |
Trening modelu:
|
1 2 3 4 5 6 7 8 9 10 11 |
history <- model %>% fit( x_train, y_train, batch_size = BATCH_SIZE, epochs = EPOCHS, verbose = VERBOSE, validation_split = 0.2 ) plot(history) |
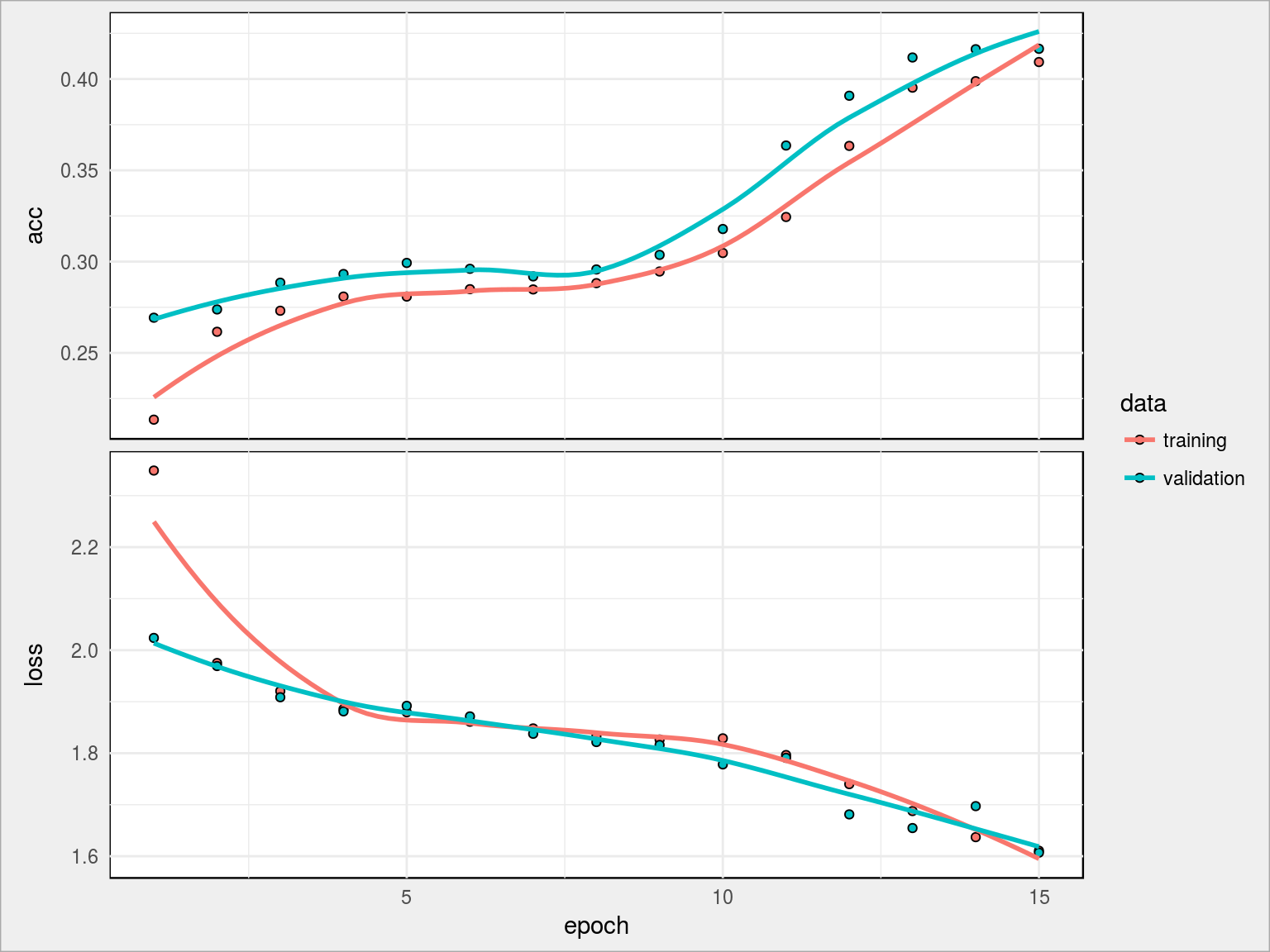
Tutaj z kolei widać, że 15 epochów to jeszcze trochę mało (krzywe nie wypłaszczyły się w całości, widać potencjał dla kolejnych kilku epochów). Osiągnęliśmy tym razem 41.65% dokładności. Wynik jest gorszy, ale zwróćcie uwagę że mniejsza była liczba możliwych do obliczenia parametrów.
Model 3
Dodajemy zatem jeszcze jedną warstwę i zwiększamy znacznie liczbę neuronów:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
model <- keras_model_sequential() %>% # architektura sieci: layer_dense(units = 32, activation = 'relu', input_shape = c(784)) %>% layer_dense(units = 64, activation = 'relu') %>% layer_dense(units = 10, activation = 'softmax') %>% # kompilacja modelu: compile( loss = 'categorical_crossentropy', optimizer = optimizer_rmsprop(), metrics = c('accuracy') ) summary(model) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
## ___________________________________________________________________________ ## Layer (type) Output Shape Param # ## =========================================================================== ## dense_4 (Dense) (None, 32) 25120 ## ___________________________________________________________________________ ## dense_5 (Dense) (None, 64) 2112 ## ___________________________________________________________________________ ## dense_6 (Dense) (None, 10) 650 ## =========================================================================== ## Total params: 27,882 ## Trainable params: 27,882 ## Non-trainable params: 0 ## ___________________________________________________________________________ |
|
1 2 3 4 5 6 7 8 9 10 11 |
history <- model %>% fit( x_train, y_train, batch_size = BATCH_SIZE, epochs = EPOCHS, verbose = VERBOSE, validation_split = 0.2 ) plot(history) |
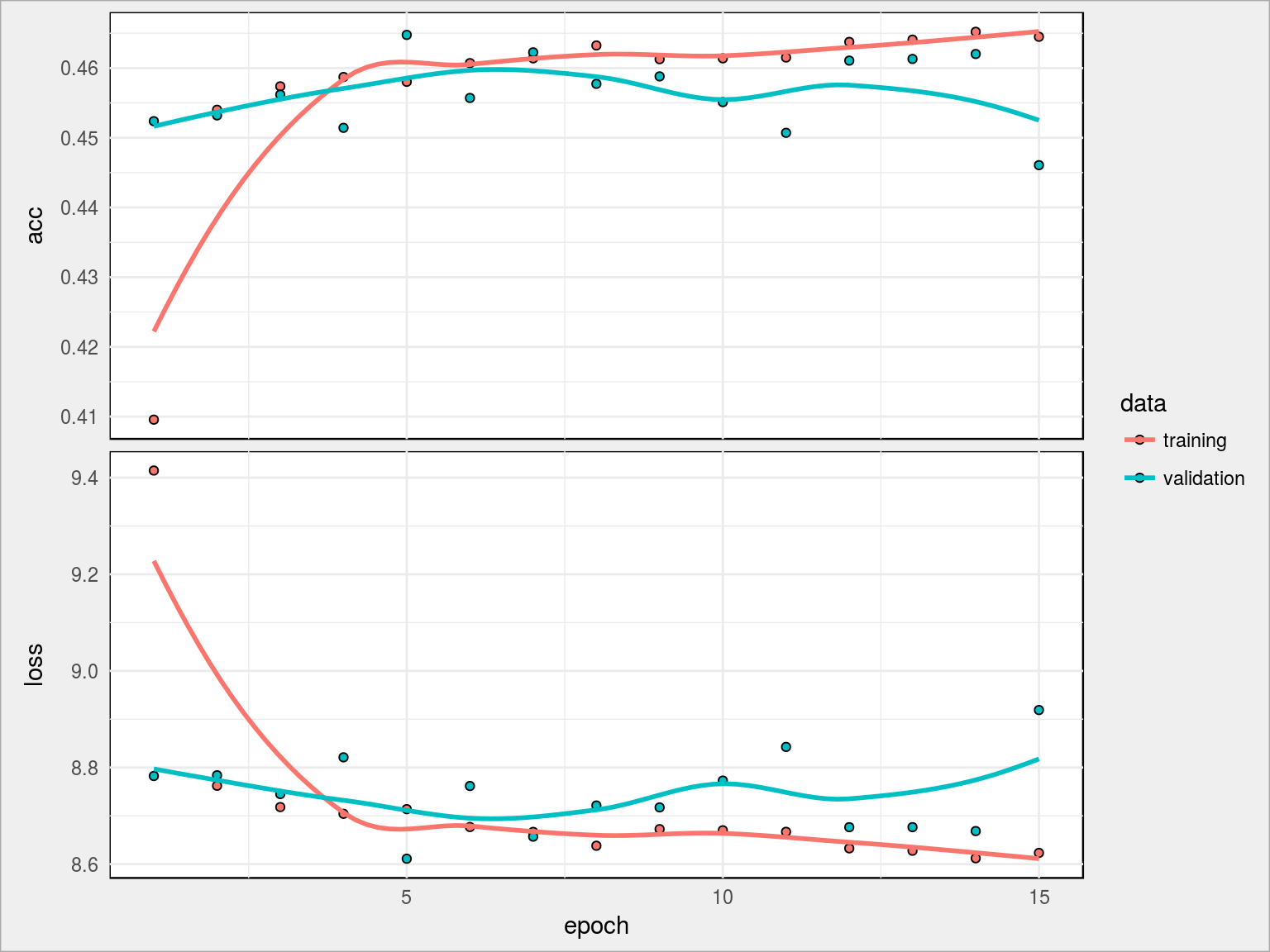
Tym razem widzimy ciekawostkę – krzywe acc od początku są na podobnym poziomie, kolejne iteracje nie przynoszą widocznej poprawy wyniku. Sam wynik też jest mało zadowalający – 44.61%. Mamy do czynienia z sytuacją opisaną wyżej (overfitting): acc rośnie, val_acc maleje. Trzeba zatem coś zrobić z siecią.
Dodamy warstwy dropout, które przepuszczają tylko część danych (wskazany procent). Jest to dobry sposób na unikniecie przeuczenia sieci. Czy zadziała w naszej architekturze?
Model 4
Trzy warstwy neuronów, przeplatane warstwami dropout:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
model <- keras_model_sequential() %>% # architektura sieci: layer_dense(units = 128, activation = 'relu', input_shape = c(784)) %>% layer_dropout(rate = 0.5) %>% layer_dense(units = 64, activation = 'relu') %>% layer_dropout(rate = 0.5) %>% layer_dense(units = 32, activation = 'relu') %>% layer_dropout(rate = 0.5) %>% layer_dense(units = 10, activation = 'softmax') %>% # kompilacja modelu: compile( loss = 'categorical_crossentropy', optimizer = optimizer_rmsprop(), metrics = c('accuracy') ) summary(model) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
## ___________________________________________________________________________ ## Layer (type) Output Shape Param # ## =========================================================================== ## dense_7 (Dense) (None, 128) 100480 ## ___________________________________________________________________________ ## dropout_1 (Dropout) (None, 128) 0 ## ___________________________________________________________________________ ## dense_8 (Dense) (None, 64) 8256 ## ___________________________________________________________________________ ## dropout_2 (Dropout) (None, 64) 0 ## ___________________________________________________________________________ ## dense_9 (Dense) (None, 32) 2080 ## ___________________________________________________________________________ ## dropout_3 (Dropout) (None, 32) 0 ## ___________________________________________________________________________ ## dense_10 (Dense) (None, 10) 330 ## =========================================================================== ## Total params: 111,146 ## Trainable params: 111,146 ## Non-trainable params: 0 ## ___________________________________________________________________________ |
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# trening modelu history <- model %>% fit( x_train, y_train, batch_size = BATCH_SIZE, epochs = EPOCHS, verbose = VERBOSE, validation_split = 0.2 ) plot(history) |
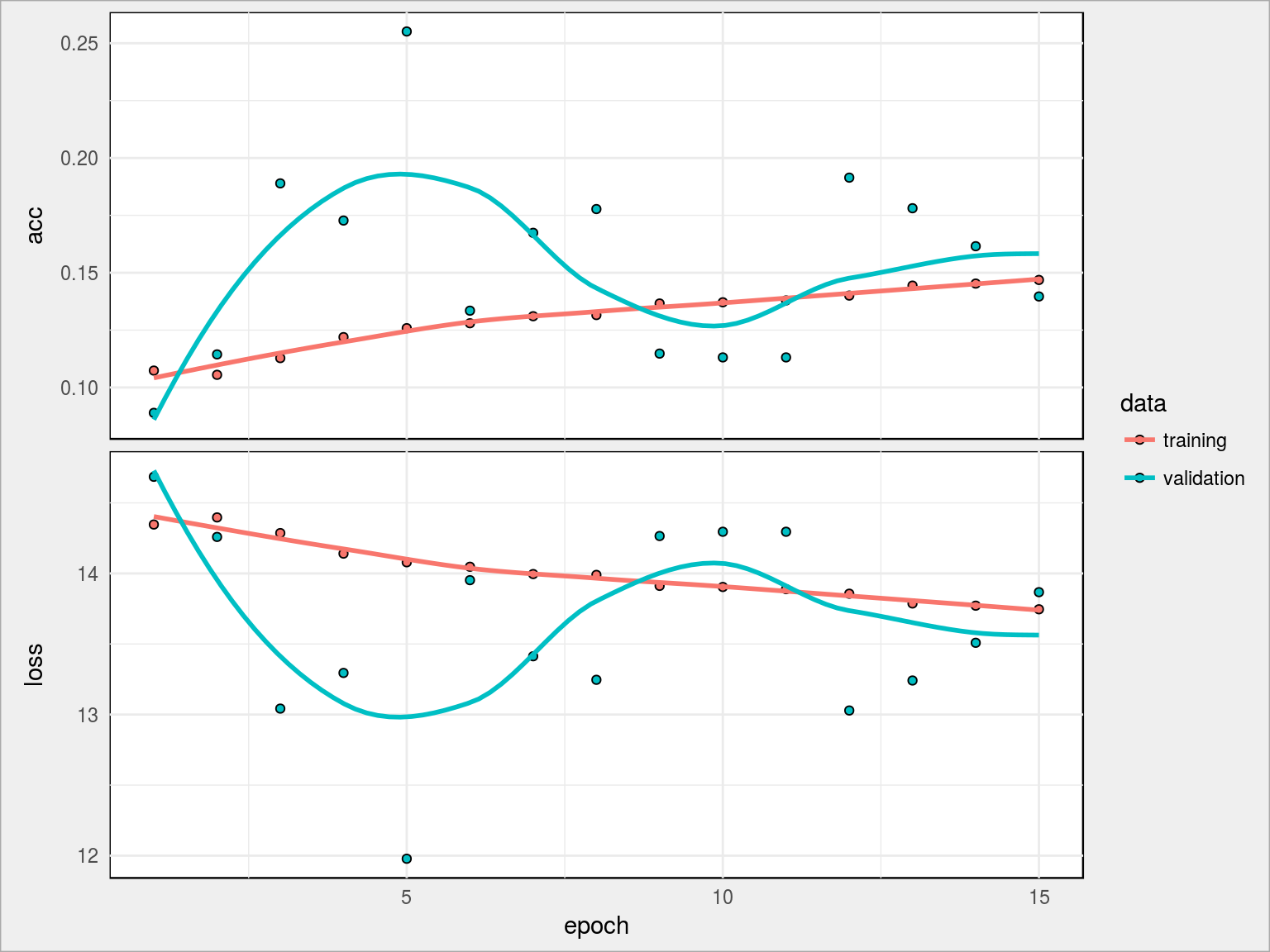
Po 15 epochach trudno powiedzieć, czy pomogło – osiągnęliśmy jeszcze gorszy wynik (13.96%), ale widać że krzywe się nie wypłaszczyły. Co ciekawe – zarówno krzywe acc jaki i loss są od siebie sporo oddalone, co nie jest zdrowe. Mamy ponad 111 tysięcy parametrów, którymi można kręcić i na nic to… Jak krew w piach.
Spróbujmy jednak czego innego – z wartości opisujących każdy punkt z zakresu 0-255 przejdźmy na zakres 0-1. Zwykłe przeskalowanie danych źródłowych. W zasadzie nie powinno niczego zmienić, prawda?
Model 4b
Dane znormalizowane do przedziału [0, 1], architektura sieci jak w modelu 4.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
x_train <- x_train / 255 model <- keras_model_sequential() %>% # architektura sieci: layer_dense(units = 128, activation = 'relu', input_shape = c(784)) %>% layer_dropout(rate = 0.5) %>% layer_dense(units = 64, activation = 'relu') %>% layer_dropout(rate = 0.5) %>% layer_dense(units = 32, activation = 'relu') %>% layer_dropout(rate = 0.5) %>% layer_dense(units = 10, activation = 'softmax') %>% # kompilacja modelu: compile( loss = 'categorical_crossentropy', optimizer = optimizer_rmsprop(), metrics = c('accuracy') ) summary(model) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
## ___________________________________________________________________________ ## Layer (type) Output Shape Param # ## =========================================================================== ## dense_11 (Dense) (None, 128) 100480 ## ___________________________________________________________________________ ## dropout_4 (Dropout) (None, 128) 0 ## ___________________________________________________________________________ ## dense_12 (Dense) (None, 64) 8256 ## ___________________________________________________________________________ ## dropout_5 (Dropout) (None, 64) 0 ## ___________________________________________________________________________ ## dense_13 (Dense) (None, 32) 2080 ## ___________________________________________________________________________ ## dropout_6 (Dropout) (None, 32) 0 ## ___________________________________________________________________________ ## dense_14 (Dense) (None, 10) 330 ## =========================================================================== ## Total params: 111,146 ## Trainable params: 111,146 ## Non-trainable params: 0 ## ___________________________________________________________________________ |
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# trening modelu history <- model %>% fit( x_train, y_train, batch_size = BATCH_SIZE, epochs = EPOCHS, verbose = VERBOSE, validation_split = 0.2 ) plot(history) |
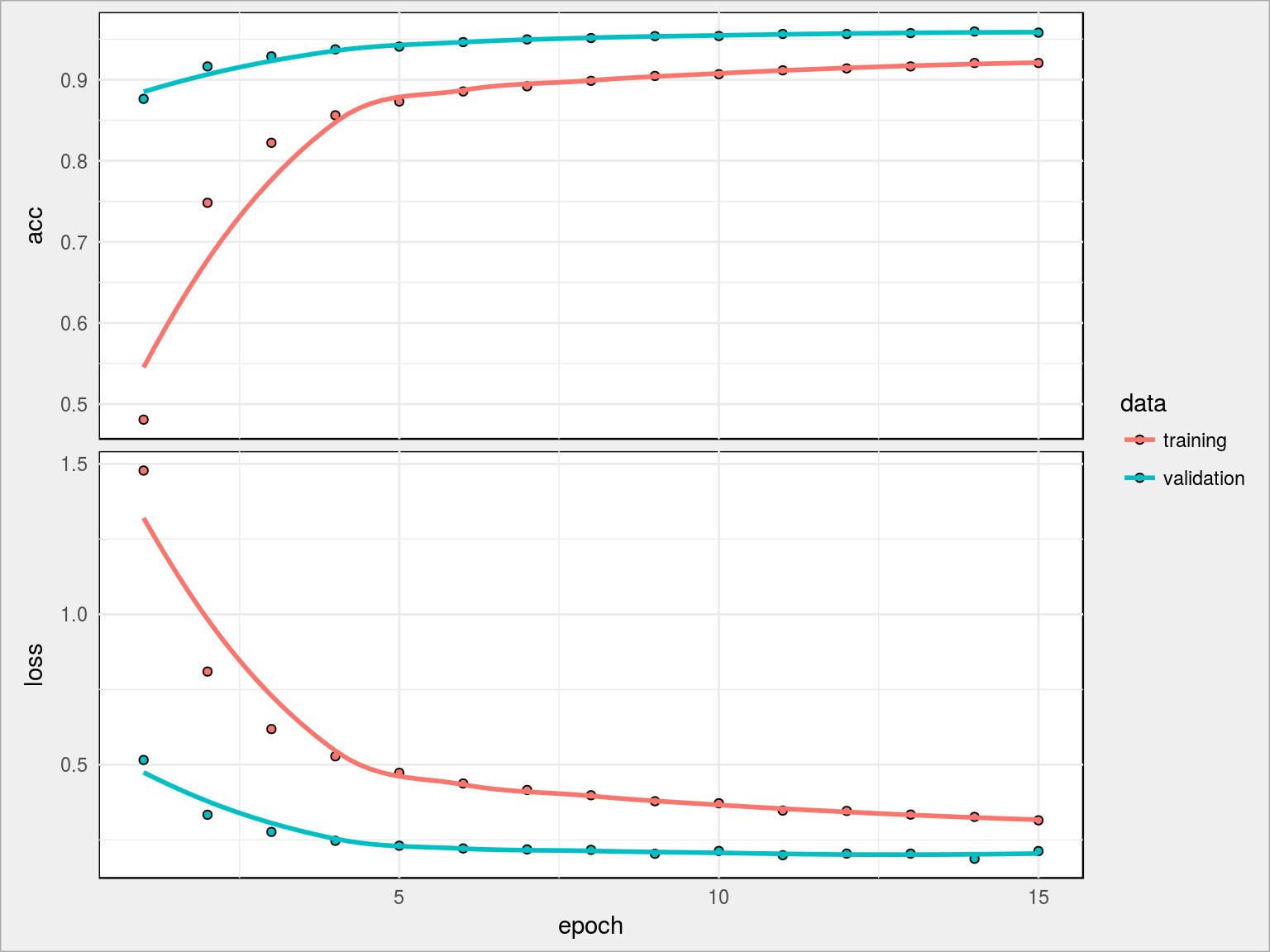
Architektura pozostała bez zmian, zmienione zostały (tylko przeskalowane!) wartości cech. Uzysk jest jak widać olbrzymi, mamy najlepszy dotychczasowy wynik – val_acc rzędu 95.81%, acc 92.07%. Szok i niedowierzanie!
Zwiększmy zatem dwukrotnie wielkość wszystkich warstw:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
model <- keras_model_sequential() %>% # architektura sieci: layer_dense(units = 256, activation = 'relu', input_shape = c(784)) %>% layer_dropout(rate = 0.5) %>% layer_dense(units = 128, activation = 'relu') %>% layer_dropout(rate = 0.5) %>% layer_dense(units = 64, activation = 'relu') %>% layer_dropout(rate = 0.5) %>% layer_dense(units = 10, activation = 'softmax') %>% # kompilacja modelu: compile( loss = 'categorical_crossentropy', optimizer = optimizer_rmsprop(), metrics = c('accuracy') ) summary(model) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
## ___________________________________________________________________________ ## Layer (type) Output Shape Param # ## =========================================================================== ## dense_15 (Dense) (None, 256) 200960 ## ___________________________________________________________________________ ## dropout_7 (Dropout) (None, 256) 0 ## ___________________________________________________________________________ ## dense_16 (Dense) (None, 128) 32896 ## ___________________________________________________________________________ ## dropout_8 (Dropout) (None, 128) 0 ## ___________________________________________________________________________ ## dense_17 (Dense) (None, 64) 8256 ## ___________________________________________________________________________ ## dropout_9 (Dropout) (None, 64) 0 ## ___________________________________________________________________________ ## dense_18 (Dense) (None, 10) 650 ## =========================================================================== ## Total params: 242,762 ## Trainable params: 242,762 ## Non-trainable params: 0 ## ___________________________________________________________________________ |
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# trening modelu history <- model %>% fit( x_train, y_train, batch_size = BATCH_SIZE, epochs = EPOCHS, verbose = VERBOSE, validation_split = 0.2 ) plot(history) |
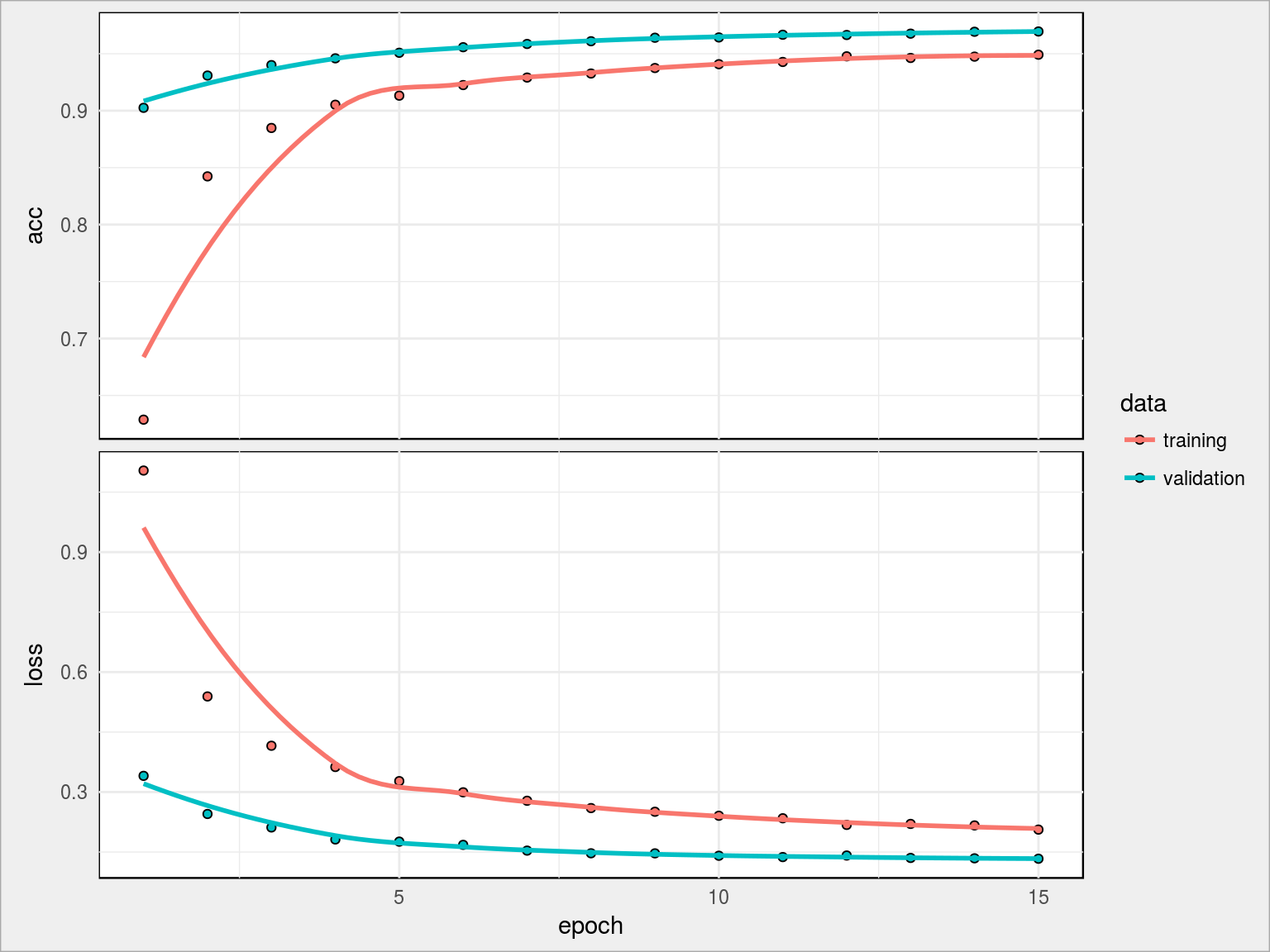
Już pierwsze epoch-i dały wynik ponad 90% dokładności. Po 15 skończyliśmy na prawie 96.95% val_acc i 94.91% acc. Można tak jeszcze trochę, na przykład dodając kolejne warstwy i zwiększając liczbę neuronów w nich, a przede wszystkim trenując sieć dłużej (dopóki rośnie val_acc). Nie da się tak jednak w nieskończoność, gdzieś jest granica (dla tego typu sieci).
Model 5
W ostatnim modelu dodajmy jeszcze jedną warstwę i dwukrornie zwiększmy liczbę neuronów w warstwach znanych z modelu 4b oraz wydłużmy dwukrotnie czas treningu. Usuniemy też jedną warstwę dropout:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
model2 <- keras_model_sequential() %>% # architektura sieci: layer_dense(units = 512, activation = 'relu', input_shape = c(784)) %>% layer_dense(units = 64, activation = 'relu') %>% layer_dropout(rate = 0.5) %>% layer_dense(units = 256, activation = 'relu') %>% layer_dropout(rate = 0.5) %>% layer_dense(units = 128, activation = 'relu') %>% layer_dropout(rate = 0.5) %>% layer_dense(units = 10, activation = 'softmax') %>% # kompilacja modelu: compile( loss = 'categorical_crossentropy', optimizer = optimizer_rmsprop(), metrics = c('accuracy') ) summary(model) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
## ___________________________________________________________________________ ## Layer (type) Output Shape Param # ## =========================================================================== ## dense_15 (Dense) (None, 256) 200960 ## ___________________________________________________________________________ ## dropout_7 (Dropout) (None, 256) 0 ## ___________________________________________________________________________ ## dense_16 (Dense) (None, 128) 32896 ## ___________________________________________________________________________ ## dropout_8 (Dropout) (None, 128) 0 ## ___________________________________________________________________________ ## dense_17 (Dense) (None, 64) 8256 ## ___________________________________________________________________________ ## dropout_9 (Dropout) (None, 64) 0 ## ___________________________________________________________________________ ## dense_18 (Dense) (None, 10) 650 ## =========================================================================== ## Total params: 242,762 ## Trainable params: 242,762 ## Non-trainable params: 0 ## ___________________________________________________________________________ |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# zwiększmy liczbę epochów EPOCHS2 <- EPOCHS * 2 # trening modelu history2 <- model2 %>% fit( x_train, y_train, batch_size = BATCH_SIZE, epochs = EPOCHS2, verbose = VERBOSE, validation_split = 0.2 ) plot(history2) |
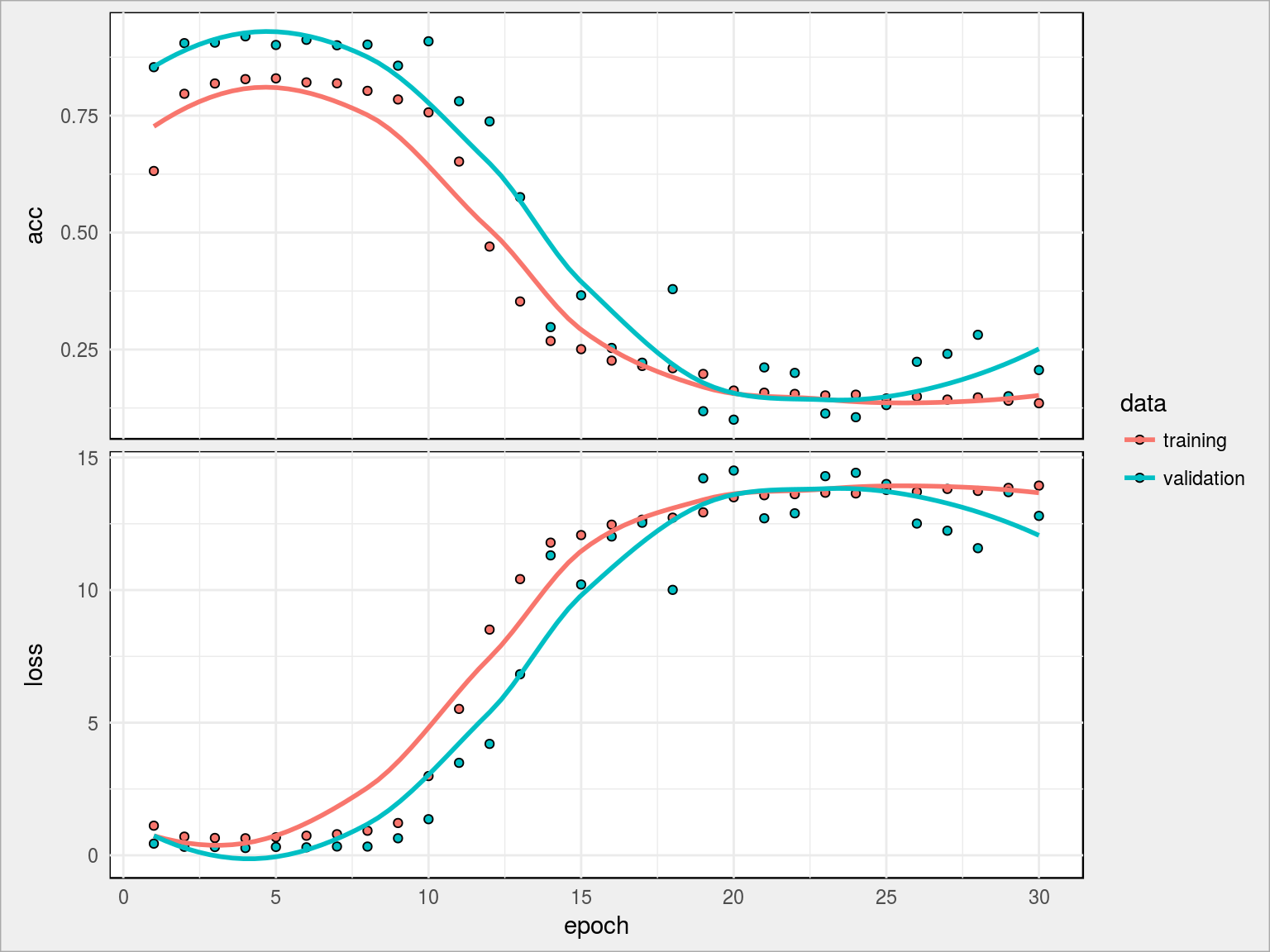
Przedobrzyliśmy. Żarło, żarło, ale zdechło. 20.61% val_acc i 13.51% acc. Może to wina zrezygnowania z jednej warstwy dropout, może sieć miała za dużo neuronów? To niestety trzeba sprawdzać empirycznie.
Warto też pokręcić parametrami compile() – przede wszystkim dobierając inny optimizer.
W kolejnych krokach użyjemy modelu 4b (dał najlepsze wyniki).
Wykorzystanie modelu
Dobrze, mamy wytrenowany model, a jak teraz mając nowe dane użyć modelu do (w tym przypadku) rozpoznawania liczb pisanych ręcznie? Dość prosto:
|
1 2 3 4 5 6 7 8 |
# wczytujemy dane testowe test <- read_csv(test_data_path) # przekształcamy je na maierz x_test <- test %>% as.matrix() # transformujemy identycznie jak dane uczące x_test <- x_test / 255 |
Mając przygotowane dane testowe (nieznane) możemy przepuścić je przez model i sprawdzić co dostaniemy na wyjściu. A dostać możemy albo konkretną klasę albo prawdopodobieństwo przypisania do niej:
|
1 2 3 4 |
pred_probs <- predict_proba(model, x_test, batch_size = 32, verbose = 1) |
Zobaczmy jak wygląda prawdopodobieństwo dla kolejnych liczb (danyych testowych):
|
1 |
head(pred_probs) |
| 0.0000000 | 0.00e+00 | 1.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 |
| 1.0000000 | 0.00e+00 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 |
| 0.0000000 | 0.00e+00 | 0.0000000 | 0.0000647 | 0.0043258 | 0.0000055 | 0.0000000 | 0.0005651 | 0.0000617 | 0.9949772 |
| 0.0006655 | 6.46e-05 | 0.0005053 | 0.0011611 | 0.3349387 | 0.0009262 | 0.0001943 | 0.0225850 | 0.0026711 | 0.6362880 |
| 0.0000000 | 1.00e-07 | 0.0000257 | 0.9998727 | 0.0000000 | 0.0000119 | 0.0000000 | 0.0000005 | 0.0000882 | 0.0000007 |
| 0.0000000 | 1.00e-07 | 0.0000332 | 0.0000402 | 0.0000003 | 0.0000000 | 0.0000000 | 0.9899057 | 0.0000031 | 0.0100174 |
No dużo liczb. Wykres poproszę! Na przykład dla szóstej w kolejności liczby:
|
1 2 3 4 5 6 7 8 |
pred_probs[6,] %>% as.data.frame() %>% gather() %>% mutate(n = row_number()-1) %>% ggplot() + geom_col(aes(as.factor(n), value), fill = "lightgreen") + geom_text(aes(as.factor(n), value, label = sprintf("%.2f%%", 100*value))) + labs(x = "Liczba", y = "Prawdopodobieństwo") |
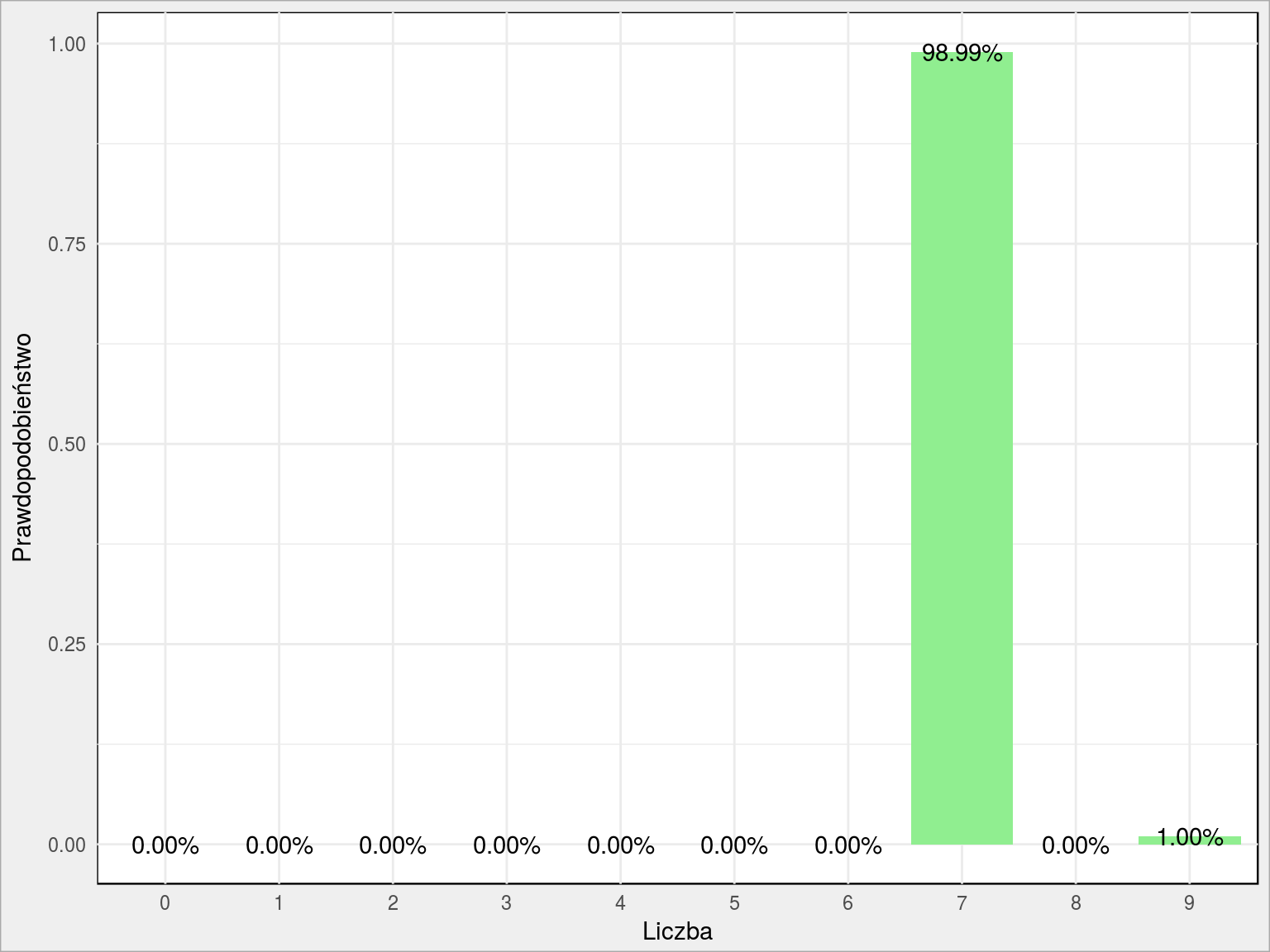
Wygląda na to, że w 98.99% jest to siódemka, a w 1.00% dziewiątka. Sama liczba wygląda tak (ta funkcja już była):
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# pokazanie wybranego wiersza (liczba) showDigit <- function(dataset=train, digit_number) { matrix1 <- dataset[digit_number, 1:dim(dataset)[2]] %>% as.numeric() %>% matrix(ncol = 28, byrow = T) matrix2 <- matrix(rep(0, 28*28), 28, 28) # odwrócenie osi Y (punkt 0,0 na górze, a nie na dole) for(i in 1:28) for(j in 1:28) matrix2[28-i, j] <- matrix1[i, j] image(t(matrix2), col = topo.colors(255), axes = FALSE) } showDigit(test, 6) |
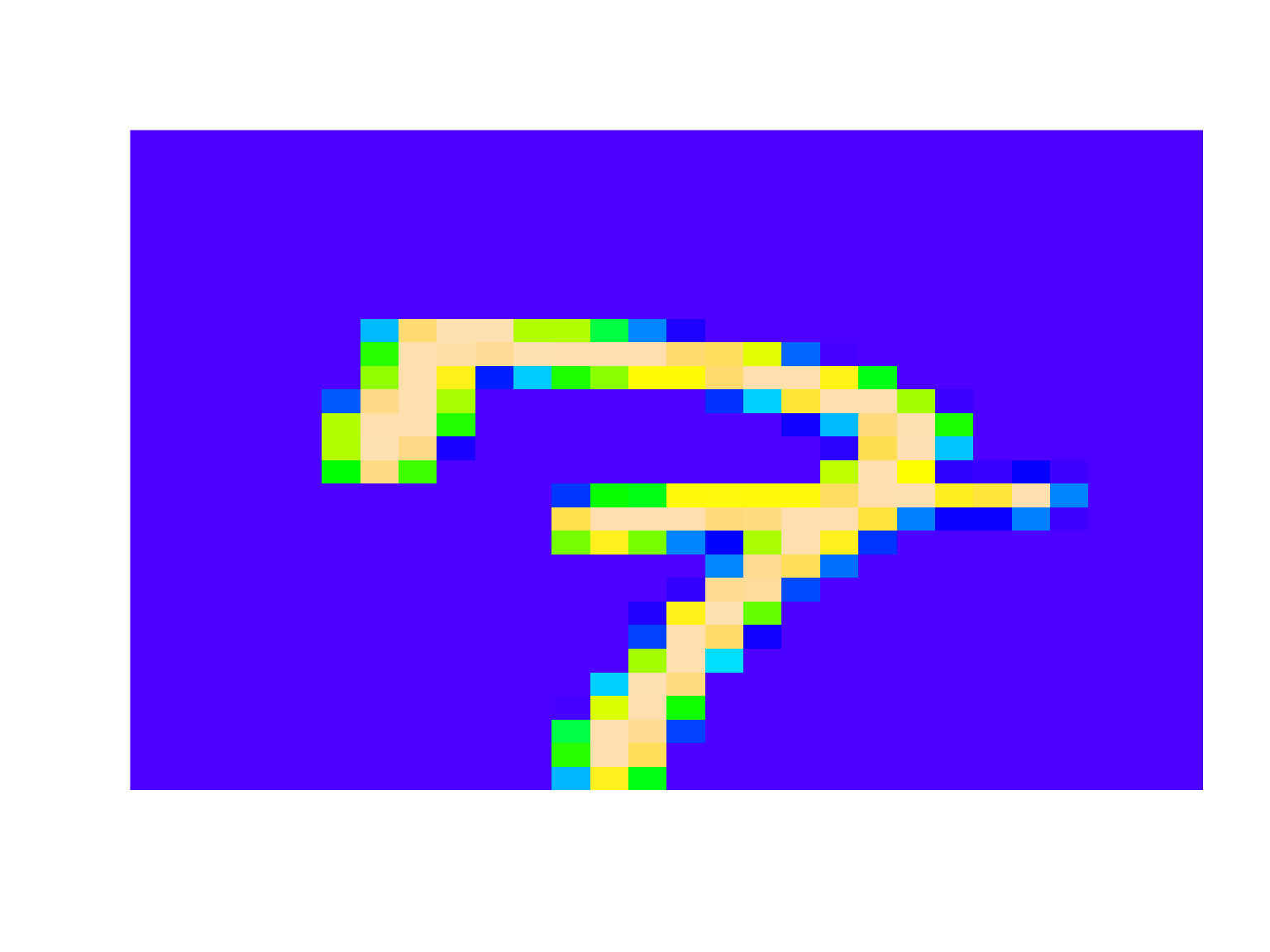
Świetnie! Jest to siódemka, ale kreseczka przecinająca nóżkę (jak to inaczej nazwać?) może zasugerować, że to niedokończona dziewiątka.
Predykcja klasy
Zamiast liczenia prawdopodobieństwa przypisania do każdej z klas możemy po prostu wybrać najbardziej prawdopodobną klasę:
|
1 2 3 4 |
pred_class <- predict_classes(model, x_test, batch_size = 32, verbose = 1) |
Jaki jest wynik dla poprzednio badanej liczby?
|
1 |
pred_class[6] |
|
1 |
## [1] 7 |
Spróbujmy poszukać liczb, z którymi był największy problem. Możemy to zrobić tylko w danych treningowych – w testowych nie mamy odpowiedzi.
|
1 2 3 4 5 6 7 8 9 10 11 |
# przewidujemy klasę dla danych treningowych pred_class <- predict_classes(model, x_train, batch_size = 32, verbose = 1) # budujemy data frame z prawdziwą i przewidzianą klasą train_df <- tibble(y_train = apply(y_train, 1, which.max) - 1, pred_class) # macierz poprawności table(train_df) |
| y_train | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 4096 | 0 | 1 | 1 | 3 | 1 | 18 | 0 | 9 | 3 |
| 1 | 0 | 4625 | 20 | 3 | 8 | 1 | 3 | 7 | 14 | 3 |
| 2 | 8 | 2 | 4083 | 12 | 8 | 0 | 7 | 22 | 30 | 5 |
| 3 | 5 | 0 | 37 | 4162 | 0 | 29 | 2 | 21 | 76 | 19 |
| 4 | 4 | 5 | 3 | 0 | 3985 | 2 | 18 | 2 | 8 | 45 |
| 5 | 10 | 2 | 3 | 29 | 4 | 3672 | 30 | 0 | 30 | 15 |
| 6 | 14 | 2 | 0 | 0 | 5 | 8 | 4102 | 0 | 6 | 0 |
| 7 | 7 | 11 | 22 | 2 | 10 | 1 | 0 | 4274 | 6 | 68 |
| 8 | 7 | 16 | 11 | 11 | 3 | 11 | 17 | 2 | 3970 | 15 |
| 9 | 9 | 3 | 1 | 16 | 42 | 8 | 1 | 26 | 11 | 4071 |
Usuńmy dobre wyniki (zaciemnią nam obraz) i zobaczmy na diagramie które liczby są ze sobą najbardziej mylone:
|
1 2 3 4 5 6 7 8 |
train_df %>% count(y_train, pred_class) %>% ungroup() %>% filter(y_train != pred_class) %>% ggplot() + geom_tile(aes(as.factor(y_train), as.factor(pred_class), fill = n)) + scale_fill_distiller(palette = "RdYlGn") + labs(x = "Liczba prawdziwa", y = "Liczba odgadnięta") |
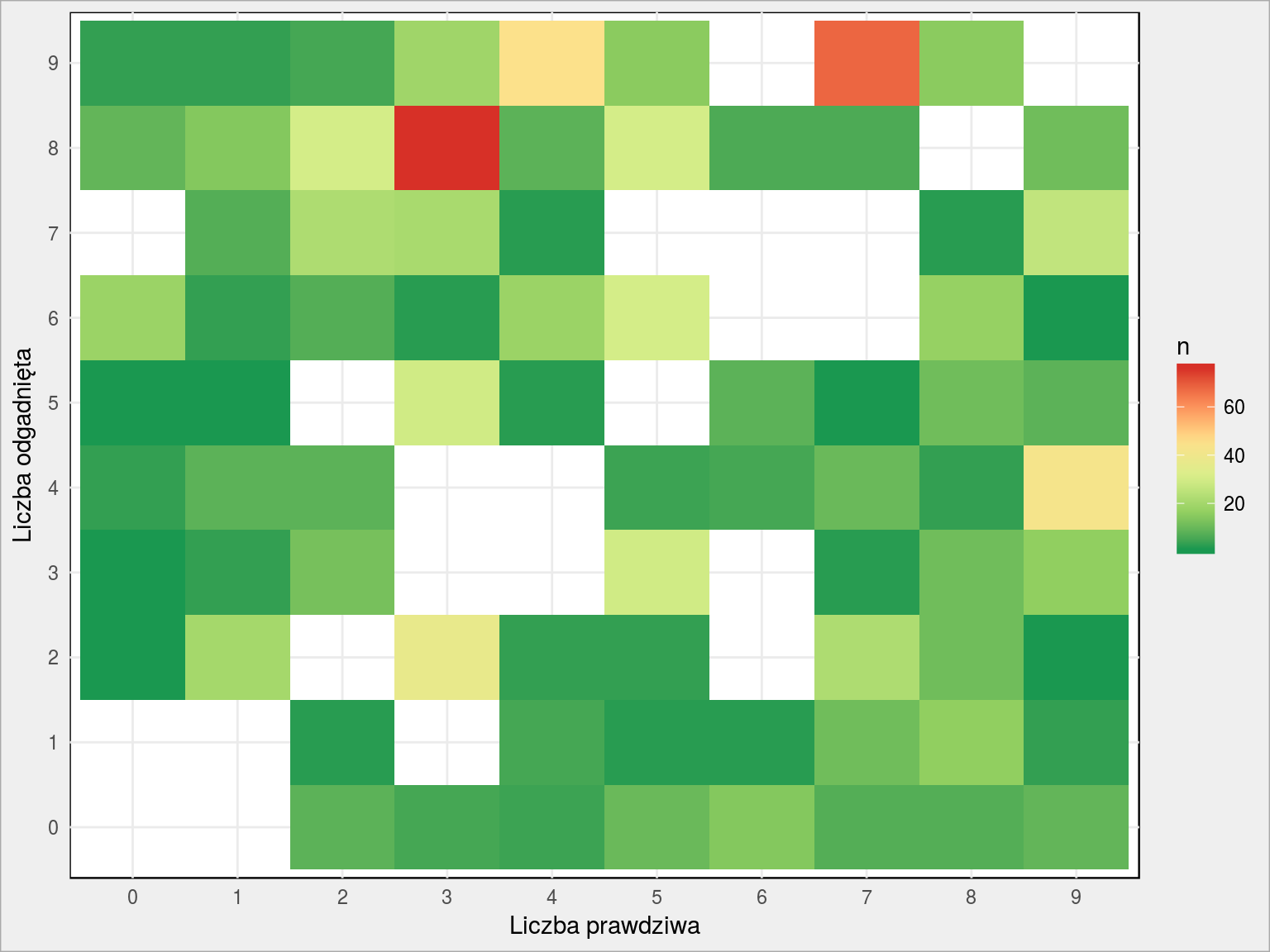
Dużo pomyłek jest pomiędzy 4 (prawdziwa liczba) i 9 (liczba rozpoznana przez sieć). Zobaczmy więc różne czwórki:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# wybieramy numery wierszy (numery kolejnych liczb) gdzie prawdziwa byla czowrka, a rozpoznano dziewiatke wybrane <- train_df %>% mutate(n = row_number()) %>% filter(y_train == 4, pred_class == 9) %>% # wystarczy nam 12 losowych probek sample_n(12) %>% pull(n) # rysujemy wszystkie te liczby plots <- list() for(i in seq_along(wybrane)) { mens <- x_train[wybrane[i], ] %>% as.data.frame() plots[[i]] <- mens %>% gather() %>% mutate(row = row_number()-1) %>% mutate(col = row%%28, row = row %/% 28) %>% ggplot() + geom_tile(aes(col, 28-row, fill=value), show.legend = FALSE) + scale_fill_gradient(low = "white", high = "black") + coord_equal() + theme_void() } do.call(grid.arrange, plots) |
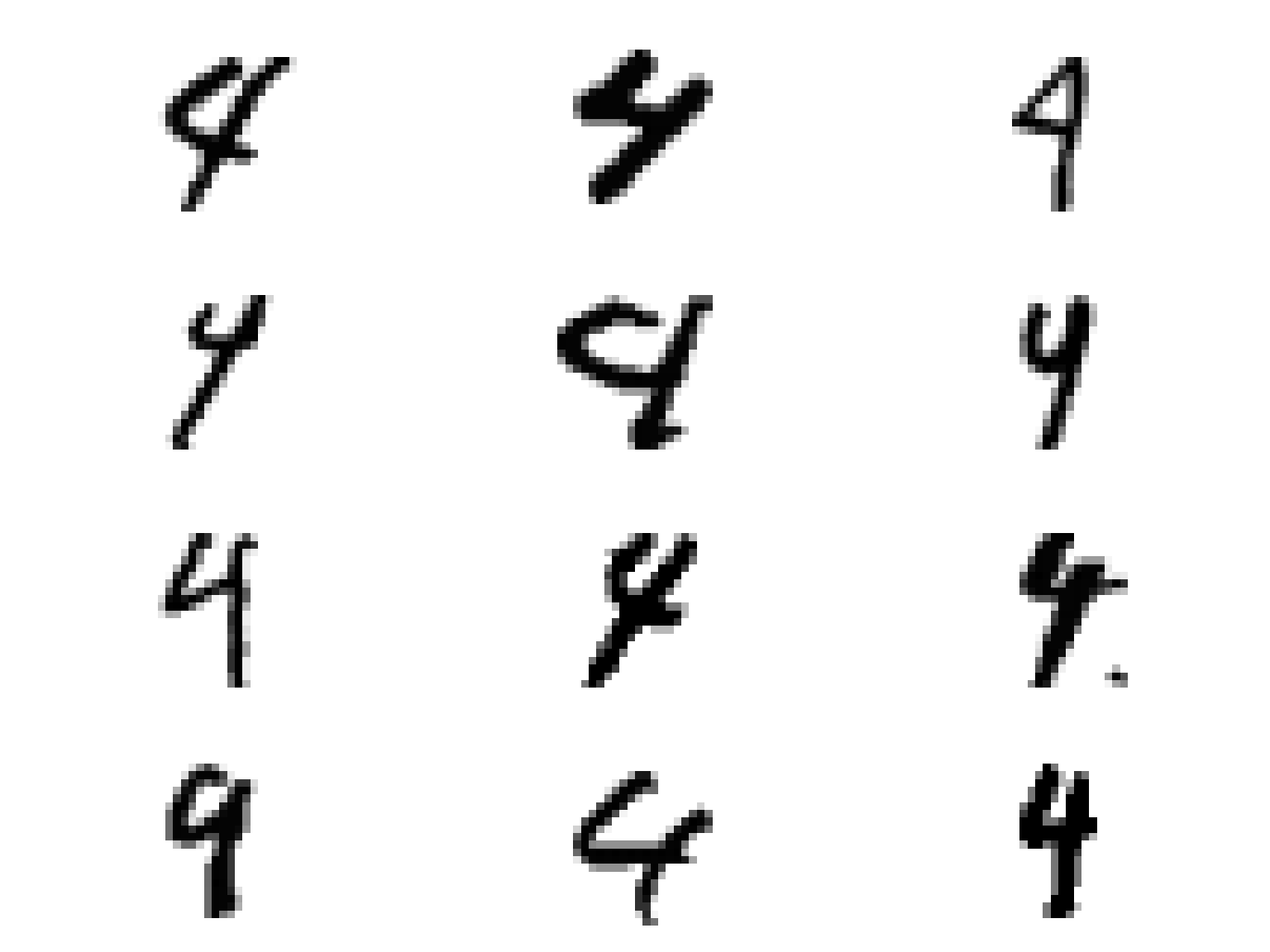
Jak widać kilka z czwórek można pomylić z dziewiątkami… wszystko się zgadza!
Podsumowanie
- zainstalowaliśmy bibliotekę Keras, która z poziomu R pozwala na budowanie sieci neuronowych opartych o TensorFlow
- zbudowaliśmy kilka modeli sieci – z różną liczbą warstw oraz neuronów w tych warstwach
- dowiedzieliśmy się co oznaczają wskaźniki acc, val_acc, loss oraz val_loss i jak na nie patrzyć
- udało nam się dość szybko zbudować sieć dającą dokładność rozpoznawania liczb na poziomie około 97%
W następnej części spróbujemy podejść do tego samego problemu traktując liczby jako obrazki (czyli macierz 28×28) a nie jako wektor liczb. Za punkt wyjścia weźmiemy 97% dokładności – rekord to zdaje się około 99.7% (co oznaczałoby jakieś 120 źle rozpoznanych liczb z naszego zbioru treningowego liczącego 42 tysiące…).