Dzisiaj trochę o grafach. Po drodze na nie się powoływałem, czasem nawet jakieś można było zobaczyć.
Ale co to są te grafy? Był wpis “edukacyjny” o metodach klasyfikacji, czas na kolejny.
Grafy to stwory matematyczne, które przydatne są na przykład w analizie sieci społecznych (wykrywanie “grup wzajemnej adoracji” albo ważnych osób wokół których skupiają się inni), logistyce (planowanie tras transportu). My zajmiemy się warszawskimi tramwajami. Bo to sieć, jakby nie było.
Dane o trasach pobrałem ze strony Warszawa.wikia.com ręcznie przepisując (Ctrl-C + Ctrl-V plus trochę Ctrl-H oraz USUŃ.ZBĘDNE.ODSTĘPY() w Excelu) do tabeli, w której w pierwszej kolumnie jest numer linii, a w drugiej – kolejne przystanki na tej linii (ich nazwy).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
library(tidyverse) library(igraph) # dane o trasach tram_routes <- read_csv2("tram_routes.csv") # dane o położeniu przystanków tram_stops <- read_csv2("tram_stops.csv") # wyznaczenie krawędzi grafu - połączeń między punktami edges <- tram_routes %>% group_by(line) %>% mutate(tram_stop_2 = lag(tram_stop)) %>% filter(!is.na(tram_stop_2), tram_stop != tram_stop_2) %>% select(from=tram_stop, to=tram_stop_2, line) # zbudowanie grafu graph_undir <- graph_from_data_frame(edges, vertices = tram_stops, directed = FALSE) |
Mamy przygotowany graf, możemy go teraz narysować. Na początek wybierzemy jeden z “layoutów” – czyli algorytmów (konkretnie Fruchterman-Reingold) do ustawiana węzłów na obrazku:
|
1 2 3 4 5 6 7 8 9 |
layout <- layout_with_fr(graph_undir) plot(graph_undir, layout = layout, vertex.label = gsub(" ", "\n", V(graph_undir)$name), vertex.size = 1, vertex.label.color = "darkgray", vertex.label.cex = 0.5, edge.color = E(graph_undir)$line) |
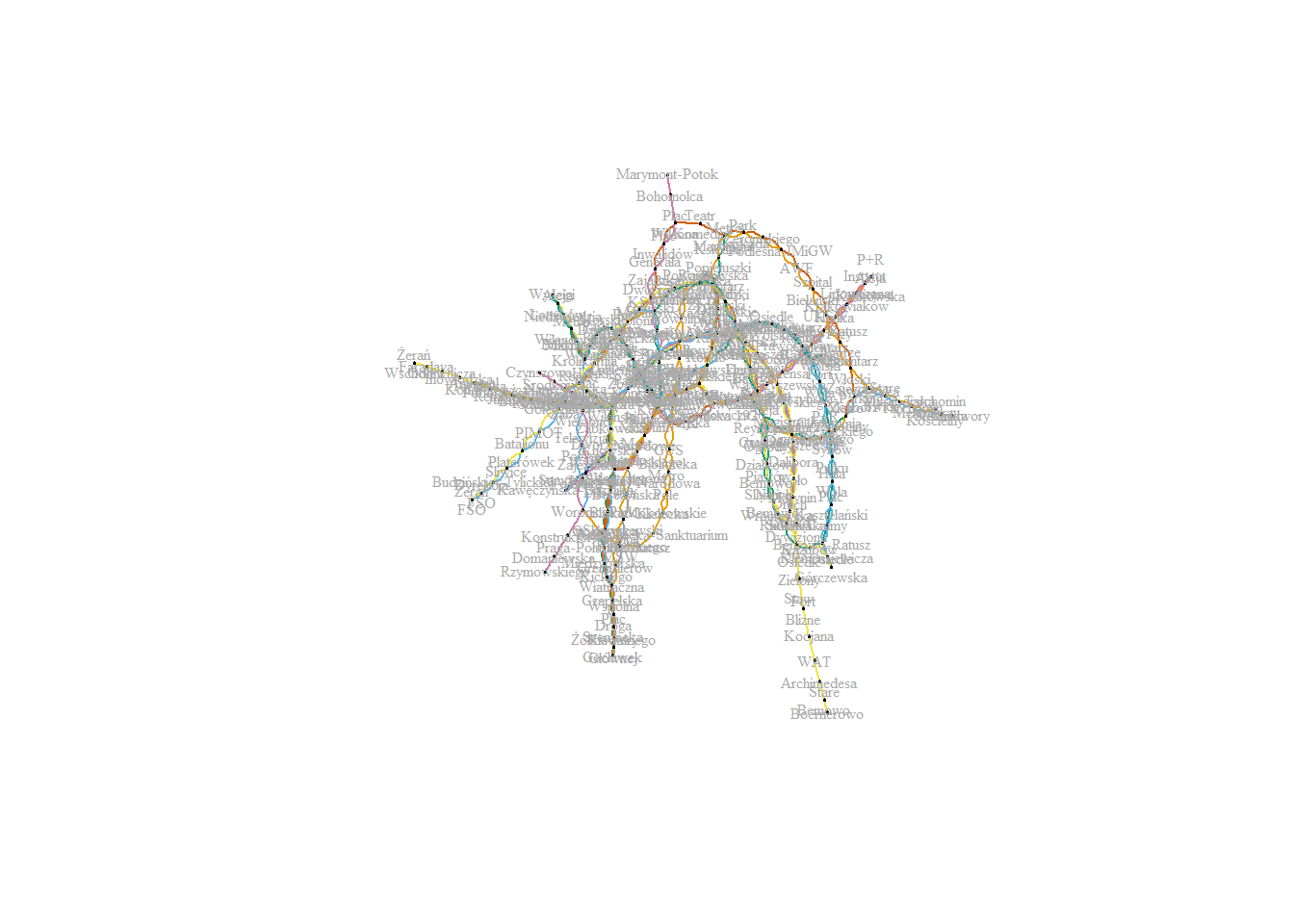
A teraz zastąpimy punkty w których zostały umieszczone węzły prawdziwym położeniem przystanków.
Dane o położeniu przystanków pobrałem ze plików wystawionych przez Zarząd Transportu Miejskiego w Warszawie, tutaj obróbka była trudniejsza, wynikowe dane to uśrednione współrzędne wszystkich przystanków o takiej samej nazwie (bo może być kilka przystanków o tej samej nazwie – w dwóch kierunkach, autobusowe i tramwajowe itp.). Pod uwagę brałem tylko przystanki występujące na liniach tramwajowych. Te dane nie są konieczne, ale pomogą w poprawnym (zgodnym z geografią) narysowaniu grafu.
|
1 2 3 4 5 6 7 8 9 10 |
layout <- as.matrix(tram_stops[,2:3]) plot(graph_undir, layout = layout, vertex.label = gsub(" ", "\n", V(graph_undir)$name), vertex.size = 1, vertex.frame.color = "black", vertex.label.color = "gray", vertex.label.cex = 0.5, edge.color = E(graph_undir)$line) |
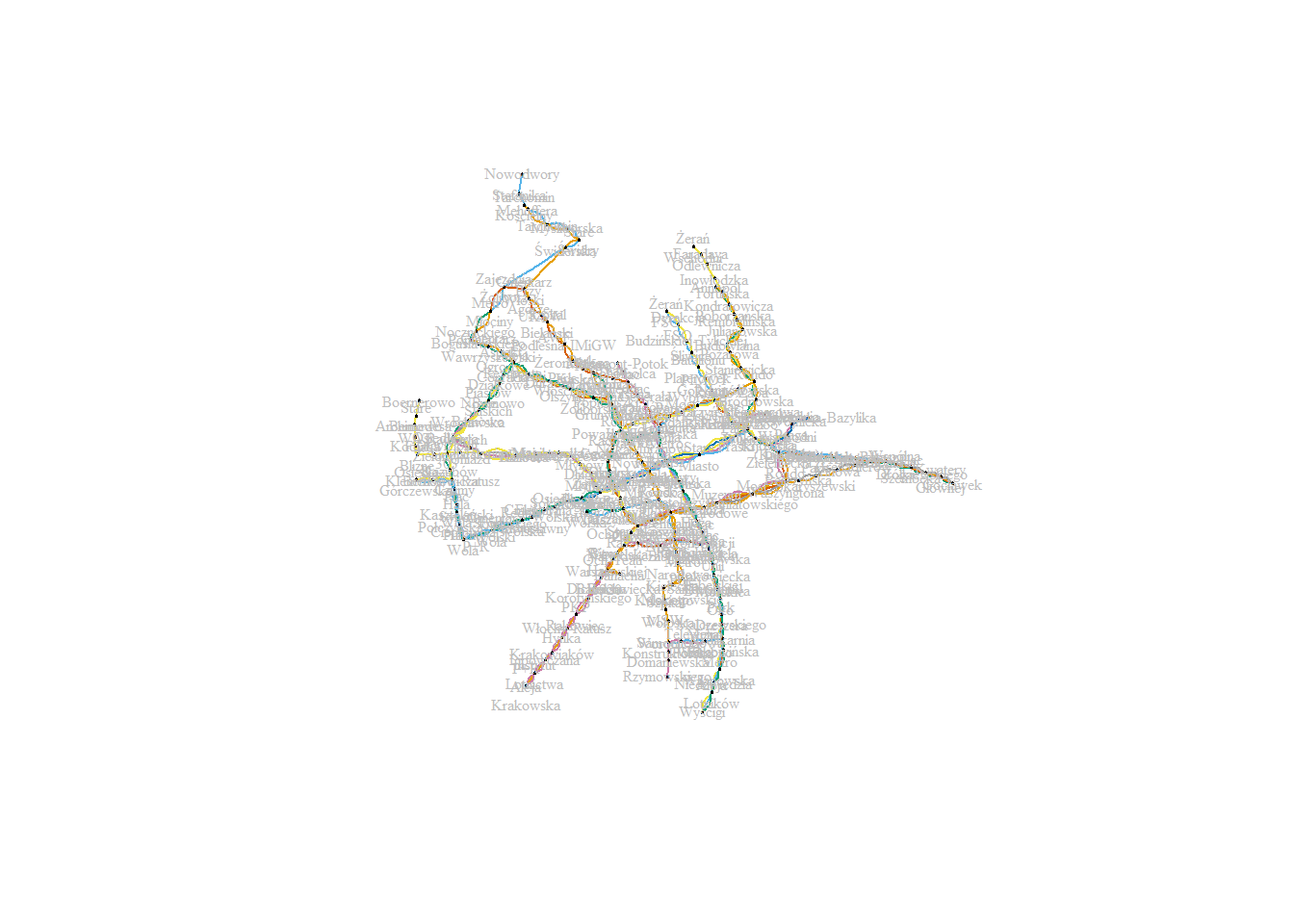
Prawda, że od razu można rozpoznać co to za miasto?
Centrality
Centrality opisuje liczbę krawędzi, które są przychodzące lub wychodzące z/do węzłów. Sieć o wysokiej koncentracji ma kilka węzłów z wieloma połączeniami, sieć o niskiej koncentracji ma wiele węzłów o podobnej liczbie krawędzi.
|
1 2 3 4 5 6 7 8 |
centr_degree(graph_undir, mode = "total")$centralization ## [1] 0.04954922 centr_clo(graph_undir, mode = "total")$centralization ## [1] 0.06612639 centr_eigen(graph_undir, directed = FALSE)$centralization ## [1] 0.925995 |
Stopień węzła
Stopień Węzła lub stopień koncentracji opisuje, jak bardzo “centralny” jest węzeł sieci, czyli ile ma wchodzących i wychodzących krawędzi, albo inaczej mówiąc – ile innych węzłów jest z nim bezpośrednio połączonych (za pośrednictwem jednej krawędzi).
|
1 2 3 4 5 6 7 8 9 10 11 12 |
graph_undir_degree <- degree(graph_undir, mode = "total") graph_undir_degree_std <- graph_undir_degree / (vcount(graph_undir) - 1) node_degree <- data.frame(degree = graph_undir_degree, degree_std = graph_undir_degree_std) %>% tibble::rownames_to_column() tram_stops <- left_join(tram_stops, node_degree, by = c("name" = "rowname")) node_degree %>% arrange(desc(degree)) %>% head(10) |
| rowname | degree | degree_std |
|---|---|---|
| Okopowa | 18 | 0.0765957 |
| Dworzec Wileński | 18 | 0.0765957 |
| Centrum | 18 | 0.0765957 |
| Metro Ratusz Arsenał | 16 | 0.0680851 |
| Dworzec Centralny | 16 | 0.0680851 |
| Rondo Radosława | 14 | 0.0595745 |
| Plac Zawiszy | 14 | 0.0595745 |
| Kijowska | 14 | 0.0595745 |
| Zajezdnia Wola | 14 | 0.0595745 |
| Plac Narutowicza | 13 | 0.0553191 |
Okopowa, Dworzec Wileński, Centrum – to przystanki, przez które przechodzi najwięcej linii tramwajowych. Jest ich po 9.
Bliskość
Bliskość węzła opisuje jego odległość do wszystkich innych węzłów. Węzeł o najwyższej bliskości jest bardziej centralny i może rozprzestrzeniać informacje na wiele innych węzłów.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
closeness <- closeness(graph_undir, mode = "total") closeness_std <- closeness / (vcount(graph_undir) - 1) node_closeness <- data.frame(closeness = closeness, closeness_std = closeness_std) %>% tibble::rownames_to_column() tram_stops <- left_join(tram_stops, node_closeness, by = c("name" = "rowname")) node_closeness %>% arrange(desc(closeness)) %>% head(10) |
| rowname | closeness | closeness_std |
|---|---|---|
| Kino Femina | 0.0004148 | 1.8e-06 |
| Metro Ratusz Arsenał | 0.0004049 | 1.7e-06 |
| Hala Mirowska | 0.0004018 | 1.7e-06 |
| Wola-Ratusz | 0.0003992 | 1.7e-06 |
| Rondo ONZ | 0.0003922 | 1.7e-06 |
| Okopowa | 0.0003915 | 1.7e-06 |
| Nowolipki | 0.0003912 | 1.7e-06 |
| Stare Miasto | 0.0003867 | 1.6e-06 |
| Muranów | 0.0003867 | 1.6e-06 |
| Plac Bankowy | 0.0003839 | 1.6e-06 |
Kino Femina to węzeł o największej “bliskości”, pozostałe są w niedalekiej okolicy. To środek miasta, a precyzyjniej – środek sieci tramwajowej. Co ciekawe, przez ten przystanek przechodzi tylko 6 linii.
Centralność
Centralność (ang. betweenness) opisuje liczbę najkrótszych ścieżek między węzłami. Węzły o dużej koncentracji znajdują się na ścieżce między wieloma innymi węzłami. W naszym przypadku znaczy to, że przystanki te są kluczowymi połączeniami między różnymi grupami węzłów, dogodne miejsca przesiadek. W sieciach społecznościowych te węzły byłyby bardzo ważne, ponieważ dzięki nim informacje mogą przechodzić do szerokiego grona odbiorców, z jednej grupy do drugiej. To w przypadku węzłów.
W przypadku krawędzi – są to te najbardziej istotne połączenia, “mosty” przenoszące informacje, łączące grupy.
Najpierw węzły:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
betweenness <- betweenness(graph_undir, directed = FALSE) betweenness_std <- betweenness / ((vcount(graph_undir) - 1) * (vcount(graph_undir) - 2) / 2) node_betweenness <- data.frame(betweenness = betweenness, betweenness_std = betweenness_std) %>% tibble::rownames_to_column() tram_stops <- left_join(tram_stops, node_betweenness, by = c("name" = "rowname")) node_betweenness %>% arrange(desc(betweenness)) %>% head(10) |
| rowname | betweenness | betweenness_std |
|---|---|---|
| Okopowa | 50269.76 | 1.828324 |
| Dworzec Centralny | 47927.15 | 1.743122 |
| Centrum | 47845.63 | 1.740158 |
| Zajezdnia Wola | 46459.45 | 1.689742 |
| Plac Zbawiciela | 45267.84 | 1.646403 |
| Hoża | 45264.19 | 1.646270 |
| Plac Konstytucji | 45083.44 | 1.639696 |
| Trasa Łazienkowska | 44979.42 | 1.635913 |
| Plac Unii Lubelskiej | 44784.34 | 1.628818 |
| Rakowiecka | 44588.58 | 1.621698 |
A teraz krawędzie:
|
1 2 3 4 5 6 7 8 9 |
edge_betweenness <- edge_betweenness(graph_undir, directed = FALSE) data.frame(edge = attr(E(graph_undir), "vnames"), betweenness = edge_betweenness) %>% tibble::rownames_to_column() %>% select(-rowname) %>% distinct() %>% arrange(desc(betweenness)) %>% head(10) |
| edge | betweenness |
|---|---|
| Reduta Wolska|Elekcyjna | 22339.624 |
| Centrum|Hoża | 11369.797 |
| Hoża|Plac Konstytucji | 11321.047 |
| Plac Konstytucji|Plac Zbawiciela | 11279.424 |
| Okopowa|Muzeum Powstania Warszawskiego | 10445.831 |
| Muzeum Powstania Warszawskiego|Rondo Daszyńskiego | 10427.894 |
| Rondo Daszyńskiego|Plac Zawiszy | 10366.649 |
| Plac Zbawiciela|Trasa Łazienkowska | 9038.885 |
| Trasa Łazienkowska|Plac Unii Lubelskiej | 8999.884 |
| Plac Unii Lubelskiej|Rakowiecka | 8960.852 |
Przez odcinek Reduta Wolska – Elekcyjna (z przystankiem Cmentarz Prawosławny po środku) przejeżdża w sumie pięć linii.
Narysujmy to. Wielkość punktu i grubość krawędzi określają ważność węzła/krawędzi:
|
1 2 3 4 5 6 7 |
plot(graph_undir, layout = layout, vertex.label = NA, vertex.size = betweenness / 10000, vertex.frame.color = "black", edge.width = edge_betweenness / 1000, edge.color = E(graph_undir)$line) |
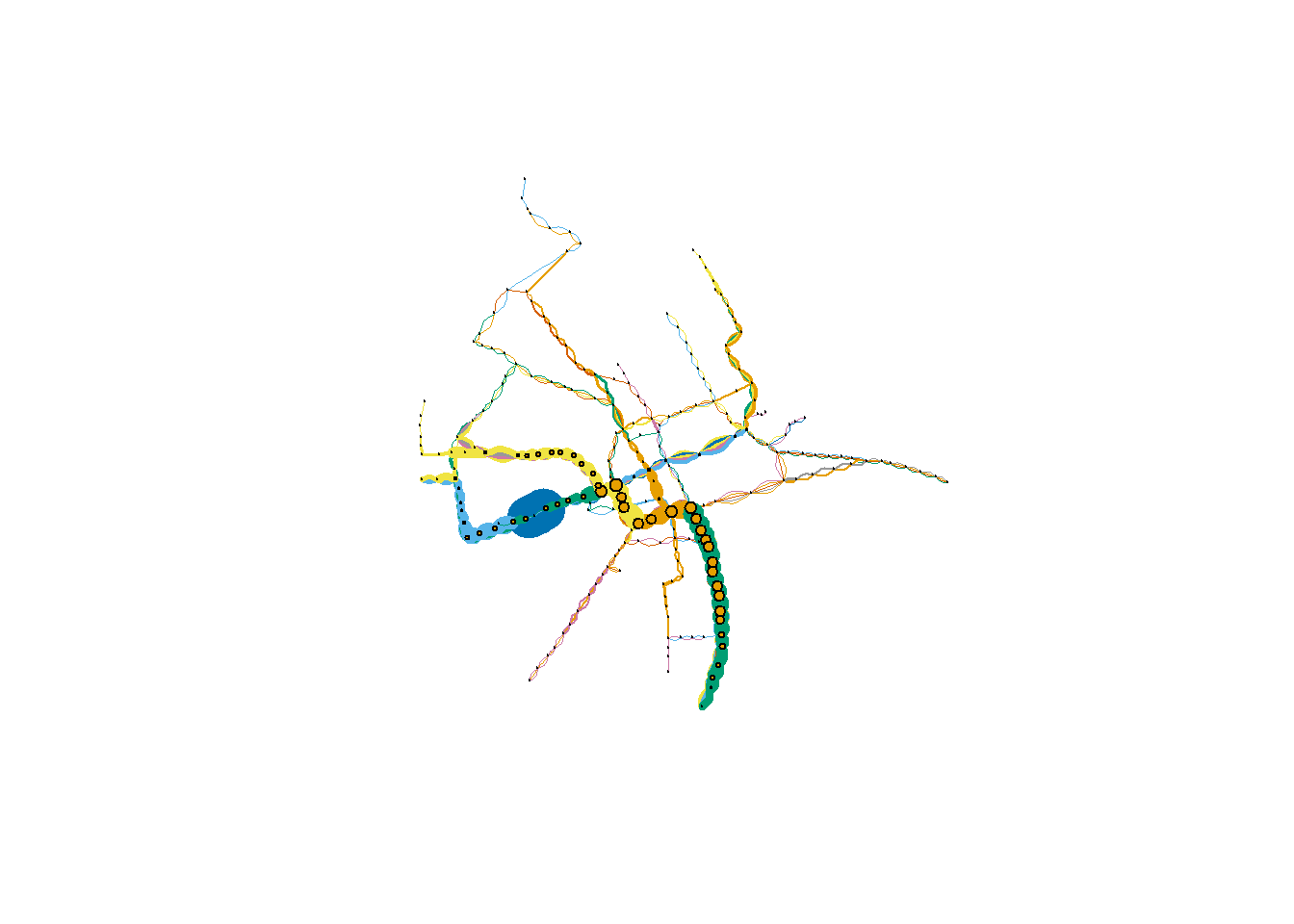
Średnica
Możemy też obliczyć najdłuższą ścieżkę pomiędzy węzłami – czyli średnicę grafu:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
diameter(graph_undir, directed = FALSE) ## [1] 42 # kopia grafu graph_undir_diameter <- graph_undir # przekątna node_diameter <- get.diameter(graph_undir_diameter, directed = FALSE) # wszystkie wierzchołki i krawędzie na szaro V(graph_undir_diameter)$color <- "grey" V(graph_undir_diameter)$size <- 2 E(graph_undir_diameter)$color <- "grey" E(graph_undir_diameter)$width <- 1 # wierzchołki i krawędzie na przekątnej - czerwone i większe V(graph_undir_diameter)[node_diameter]$color <- "red" V(graph_undir_diameter)[node_diameter]$size <- 5 E(graph_undir_diameter, path = node_diameter)$color <- "red" E(graph_undir_diameter, path = node_diameter)$width <- 5 # wierzchołki nie będące na przekątnej dostają pustą nazwę V(graph_undir_diameter)$name <- ifelse(V(graph_undir_diameter)$size == 5, V(graph_undir_diameter)$name, "") plot(graph_undir_diameter, layout = layout, vertex.label = gsub(" ", "\n", V(graph_undir_diameter)$name), vertex.size = 1, vertex.label.color = "black", vertex.label.cex = 0.8) |
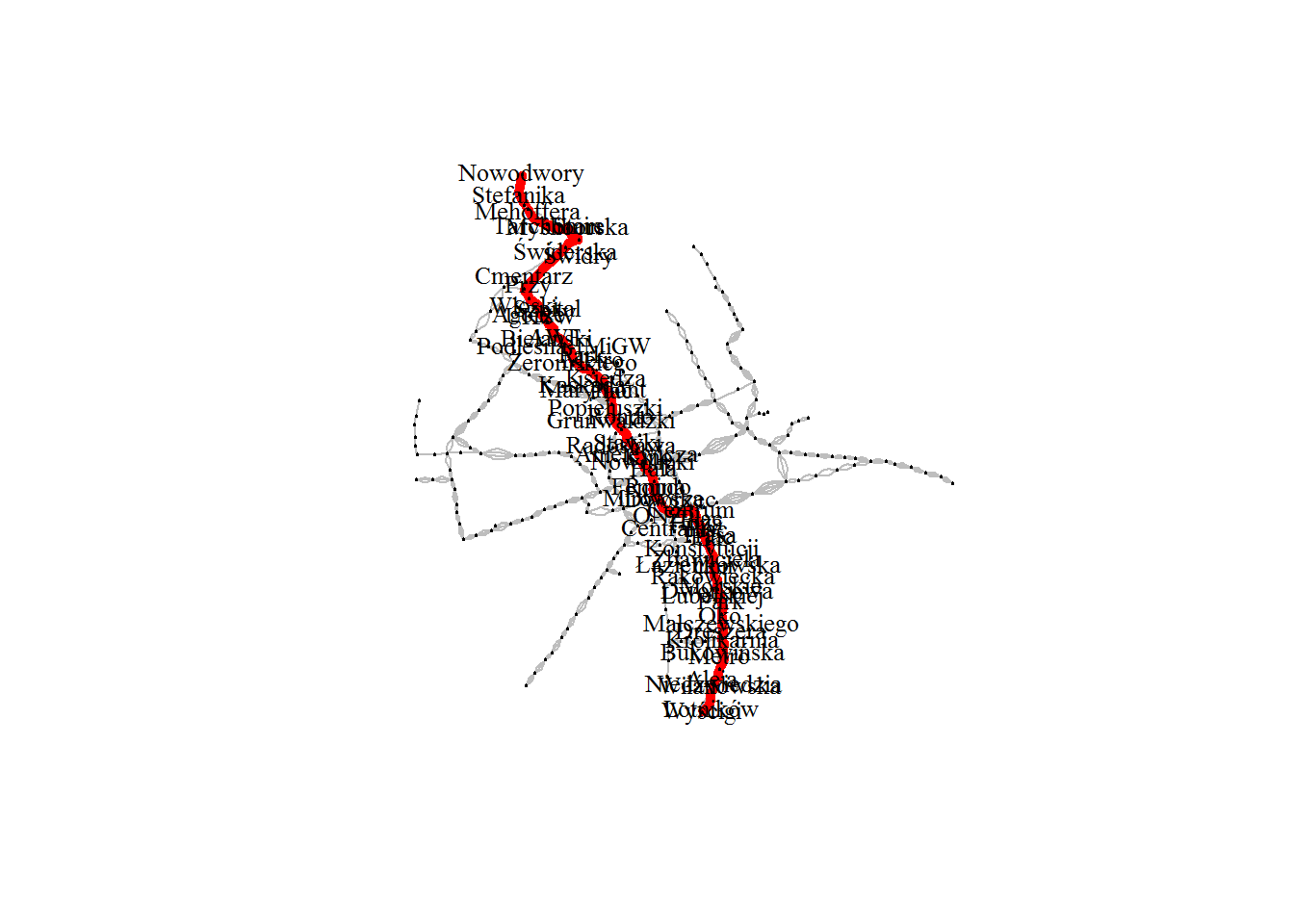
Są to połączone trasy – dwójką z Nowodworów do np. Tarchomina, przesiadka w 17, podróż na przykład do Rondo Radosława, a na koniec przesiadka w 35 i jazda do Wyścigów. Moje dziecko starsze, kochające jazdę tramwajami, byłoby szczęśliwe!
Przejście
Przejście (ang. transitivity) to miara prawdopodobieństwa że sąsiednie wierzchołki (węzły) danego węzła są połączone ze sobą. Czasami nazywa się to również współczynnikiem klastrowania.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
transitivity(graph_undir, type = "global") ## [1] 0.05660377 transitivity <- data.frame(name = V(graph_undir)$name, transitivity = transitivity(graph_undir, type = "local")) %>% mutate(name = as.character(name)) tram_stops <- left_join(tram_stops, transitivity, by = "name") transitivity %>% arrange(desc(transitivity)) %>% head(10) |
| name | transitivity |
|---|---|
| KS Polonia | 0.3333333 |
| Zajezdnia Żoliborz | 0.1666667 |
| Świderska | 0.1666667 |
| Cmentarz Włoski | 0.1666667 |
| Ratuszowa | 0.1666667 |
| Dzielna | 0.1333333 |
| Żytnia | 0.1333333 |
| Dworzec Gdański | 0.0714286 |
| Cmentarz Żydowski | 0.0666667 |
| Ratuszowa-Zoo | 0.0666667 |
Czyli 1/3 sąsiadów przystanku “KS Polonia” jest ze sobą połączona. Sąsiedzi tego przystanku to: Dworzec Gdański, Park Traugutta i Muranowska. Mamy więc trzy możliwe połączenia. Muranowska połączona jest z Dworcem Gdańskim, tak samo jak Park Traugutta – czyli mamy dwa z trzech na tak. Park Traugutta i Muranowska nie są połączone – zatem jedno na nie.
Klastrowanie (ang. clustering)
Możemy poszukać grup w naszej sieci poprzez grupowanie węzłów w zależności od centralności (ang. betweenness) ich krawędzi:
|
1 2 3 4 5 6 7 8 9 10 11 |
ceb <- cluster_edge_betweenness(graph_undir) modularity(ceb) ## [1] 0.807952 plot(ceb, graph_undir, layout = layout, vertex.label = NA, vertex.size = 1, vertex.frame.color = "black", edge.color = E(graph_undir)$line) |
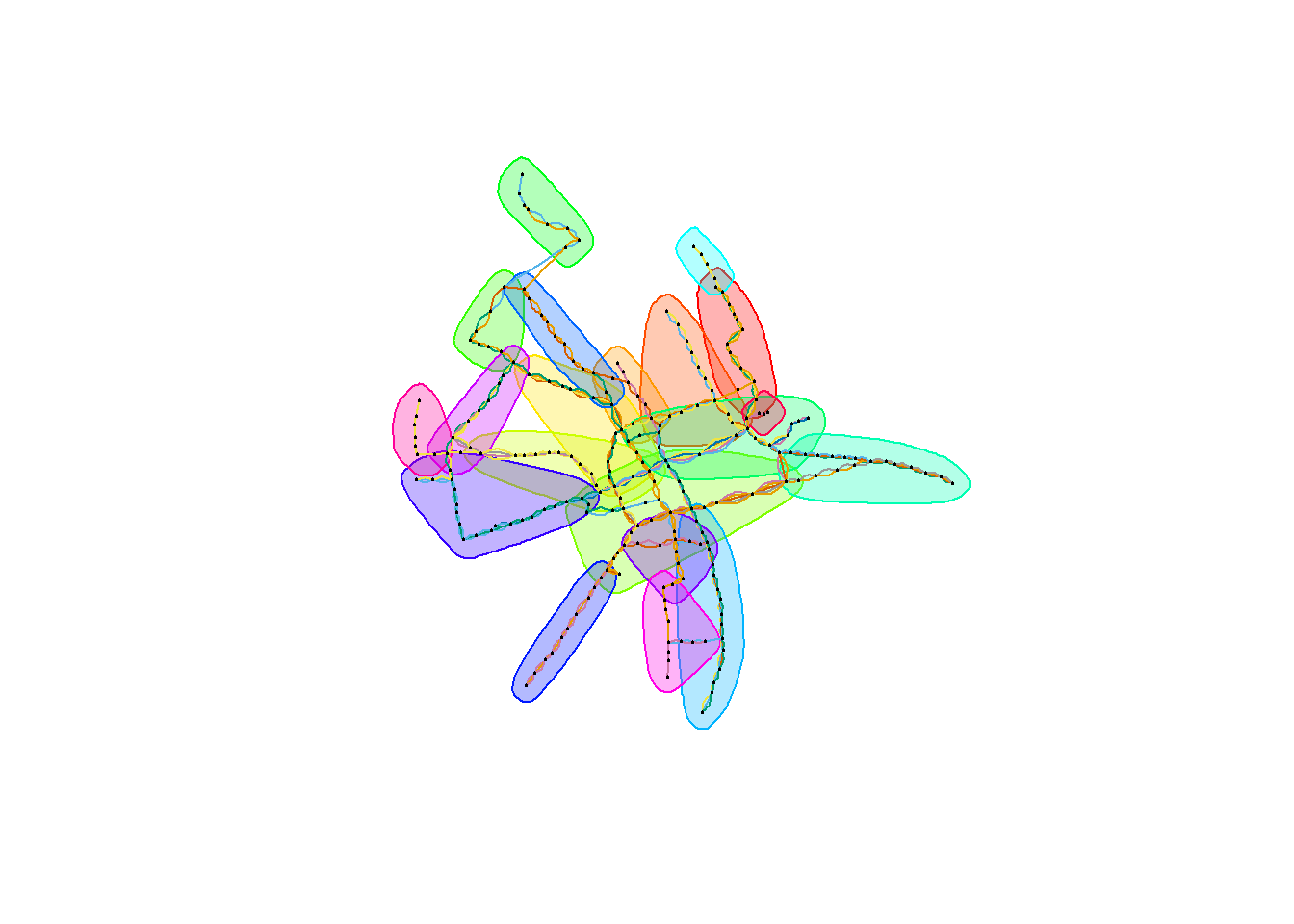
lub na podstawie propagujących etykiet (czymkolwiek by to nie było):
|
1 2 3 4 5 6 7 8 9 |
clp <- cluster_label_prop(graph_undir) plot(clp, graph_undir, layout = layout, vertex.label = NA, vertex.size = 1, vertex.frame.color = "gray", edge.color = E(graph_undir)$line) |
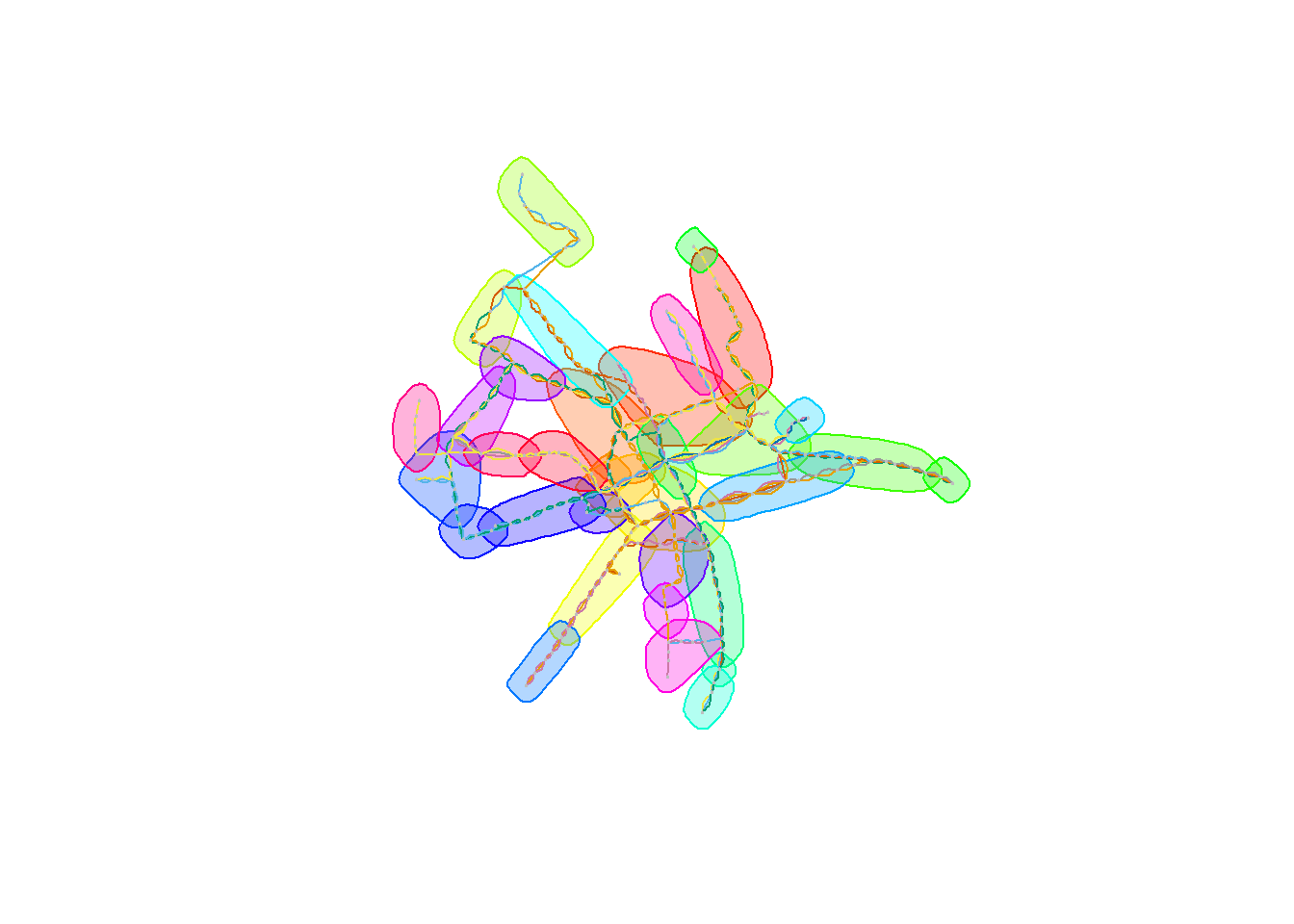
Inne metody klastrowania (albo inaczej: “wykrywania klik”“) to cluster_fast_greedy, który nie działa dla grafów, gdzie dwa węzły łączy więcej niż jedna krawędź – nie zobaczymy zatem wyniku.
Kolejna metoda to cluster_walktrap:
|
1 2 3 4 5 6 7 8 9 |
clwt <- cluster_walktrap(graph_undir) plot(clwt, graph_undir, layout = layout, vertex.label = NA, vertex.size = 1, vertex.frame.color = "gray", edge.color = E(graph_undir)$line) |
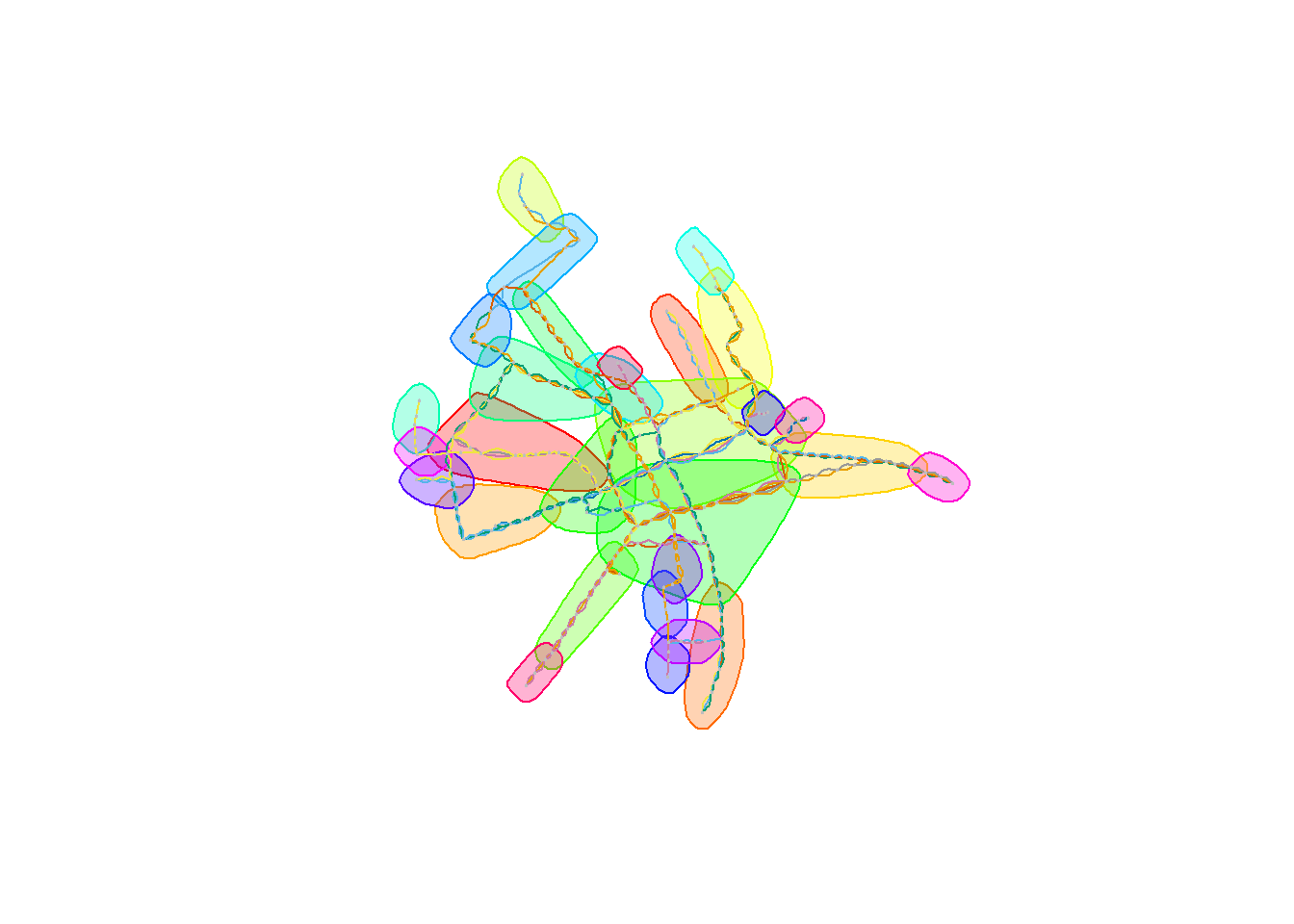
Na koniec cluster_spinglass:
|
1 2 3 4 5 6 7 8 9 |
clspg <- cluster_spinglass(graph_undir) plot(clspg, graph_undir, layout = layout, vertex.label = NA, vertex.size = 1, vertex.frame.color = "gray", edge.color = E(graph_undir)$line) |
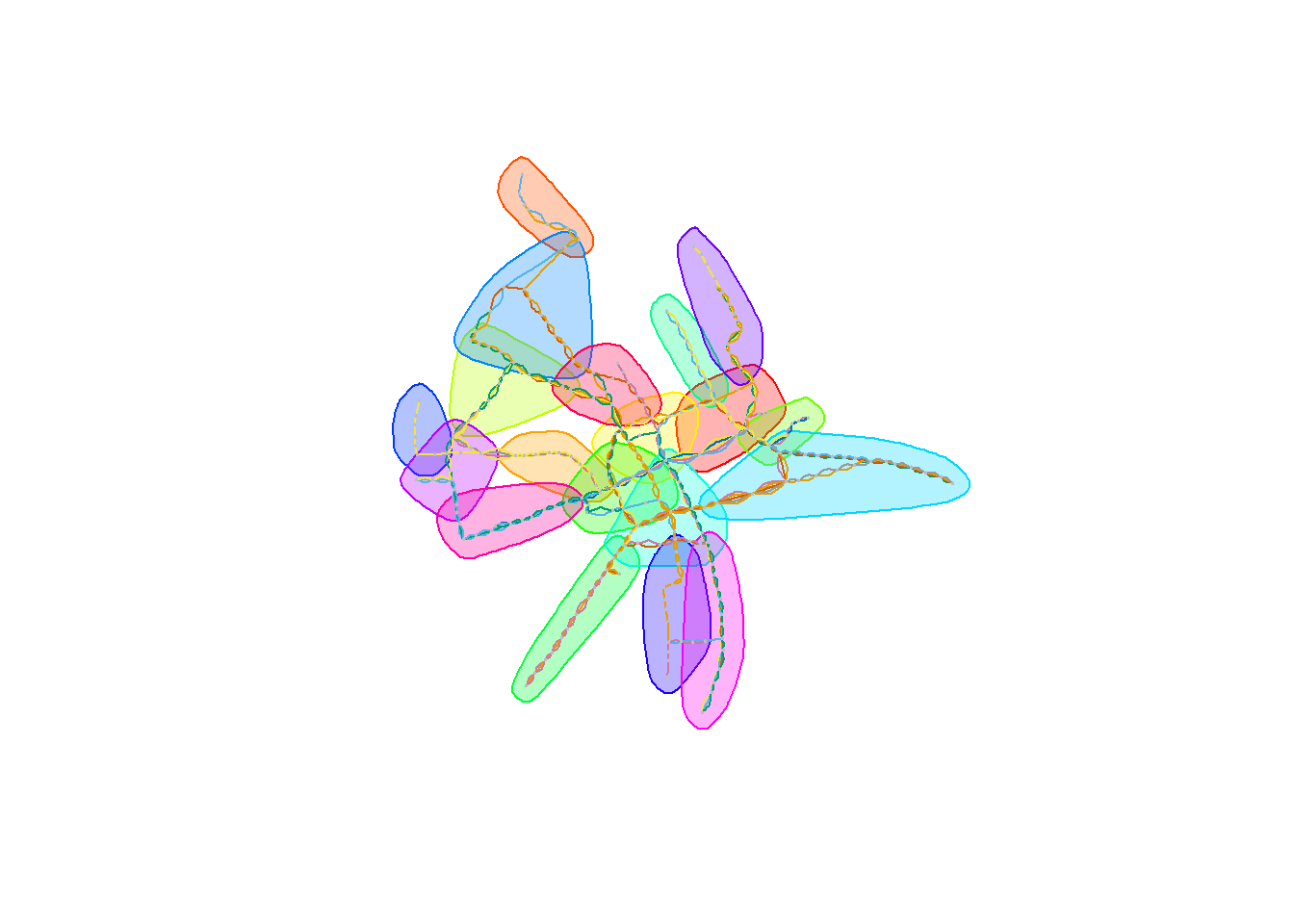
Szczegóły poszczególnych algorytmów można znaleźć w dokumentacji igraph oraz w artykułach, do których ta dokumentacja odsyła.
Wyznaczenie najkrótszej trasy
Grafy to najprostszy sposób wyznaczania najkrótszej trasy. Wagi poszczególnych krawędzi mogą określać na przykład czas przejazdu lub odległość pomiędzy wierzchołkami. Jeśli mamy grafy skierowane to krawędź A->B może mieć inną wagę niż B->A, wówczas może się okazać, że najkrótsza (albo najszybsza) droga pomiędzy dwoma wierzchołkami wydaje się być naokoło. Z tego typu algorytmów korzystają wszelakie nawigacje. Ale też inne systemy – na przykład w sieci społecznej (mając bardzo duży graf) możemy policzyć wszystkie odległości każdy z każdym i sprawdzić czy zasada “sześciu uścisków dłoni” jest prawdziwa. Jakiś czas temu Facebook opublikował tekst o tym, że owe “sześć uścisków dłoni” to obecnie coś w okolicach 2.3… ale oni mają wielki graf.
My poszukamy najkrótszej (w rozumieniu najmniejszej ilości przystanków – nie mamy czasów przejazdu pomiędzy przystankami) drogi z jednego przystanku na drugi. Wybierzmy trasę z jednego końca miasta na drugi, ale nie jakąś prostą – na przykład z przystanku Kondratowicza na Czumy:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
# kopia grafu graph_undir_path <- graph_undir # szukamy najkrótszej drogi short_path <- shortest_paths(graph_undir_path, "Kondratowicza", "Czumy") # wszystkie wierzchołki i krawędzie na szaro V(graph_undir_path)$color <- "grey" V(graph_undir_path)$size <- 2 E(graph_undir_path)$color <- "grey" E(graph_undir_path)$width <- 1 # wierzchołki i krawędzie na przekątnej - czerwone i większe V(graph_undir_path)[short_path$vpath[[1]]]$color <- "red" V(graph_undir_path)[short_path$vpath[[1]]]$size <- 5 E(graph_undir_path, path = short_path$vpath[[1]])$color <- "red" E(graph_undir_path, path = short_path$vpath[[1]])$width <- 5 # wierzchołki nie będące na trasie dostają pustą nazwę V(graph_undir_path)$name <- ifelse(V(graph_undir_path)$size == 5, V(graph_undir_path)$name, "") plot(graph_undir_path, layout = layout, vertex.label = gsub(" ", "\n", V(graph_undir_path)$name), vertex.size = 2, vertex.frame.color = "gray", vertex.label.color = "black", vertex.label.cex = 0.6, edge.color = E(graph_undir_path)$color) |
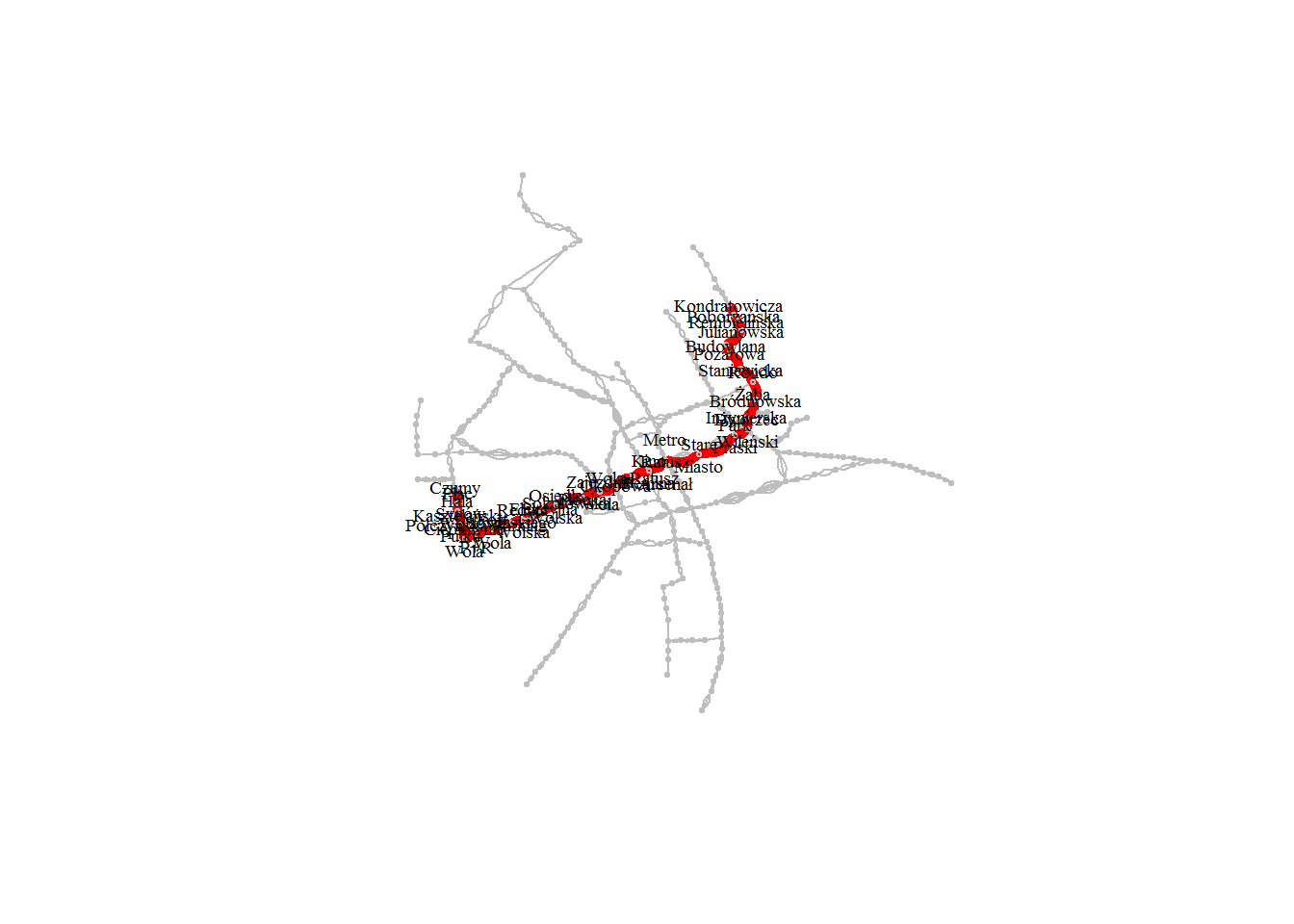
Dla porównania zamiast Czumy wybierzmy sąsiedni przystanek (jadąc od Młocin 11 jest to przystanek wcześniejszy) – Bemowo-Ratusz:
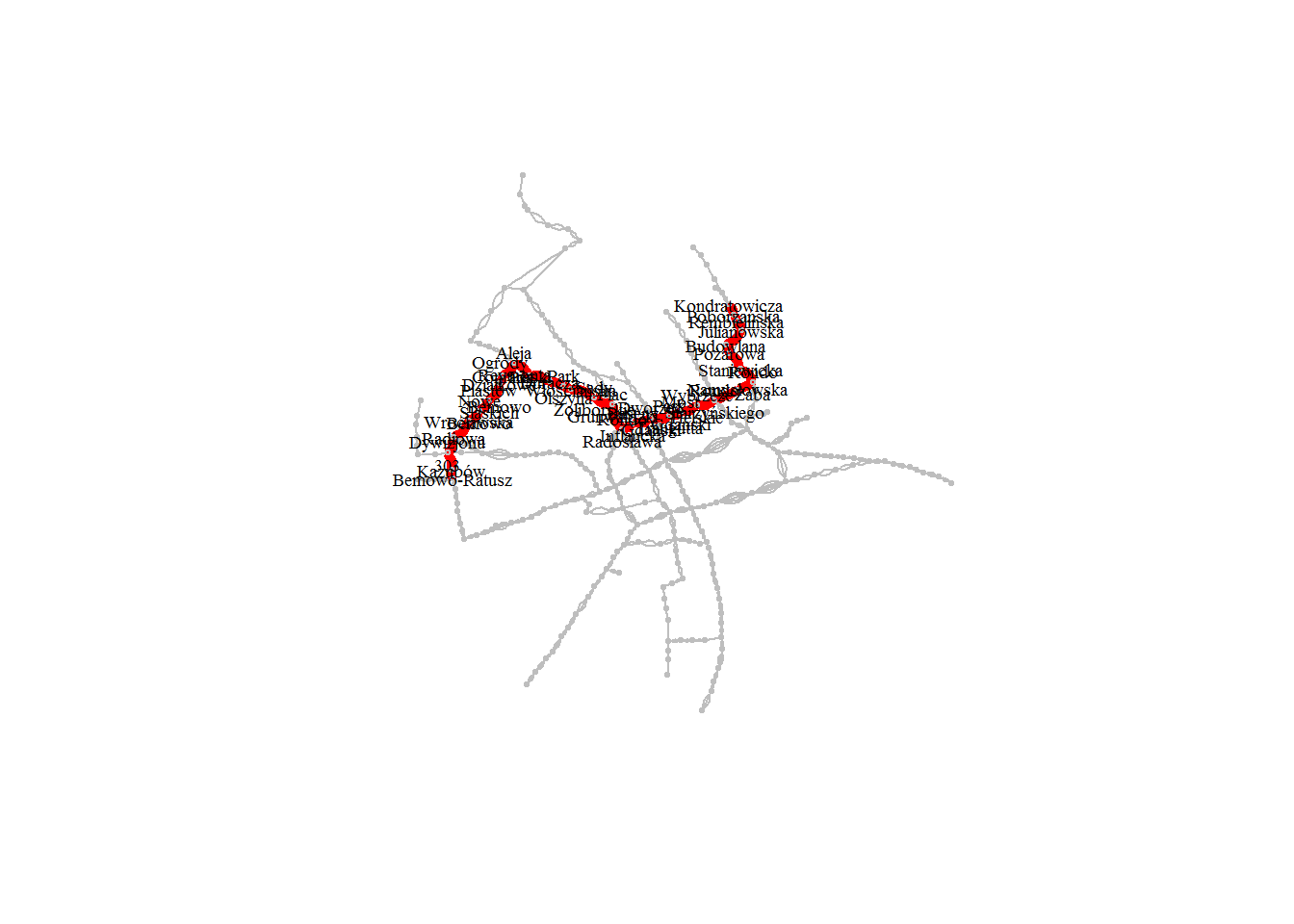
Widać, że różnica jednego przystanku diametralnie zmieniła trasę.
Grafy są fajne, prawda?
Super robota. Czekam na kolejne :)
Bliskość jest odwrotnie, im niższa tym bardziej centralny węzeł.