Którędy i jak szybko jeździ Veturilo?

Jakimi trasami poruszają się rowery Veturilo?

Czy ludzie dojeżdżają rowerem do metra?

Jak szybko jeżdżą rowery?

Czy to od czegoś zależy?

W pierwszej części opisałem skąd pobrać dane, pokazałem jak wygląda liczba rowerów Veturilo poruszających się po Warszawie (w ciągu dwóch miesięcy, ale także średnio w poszczególnych dniach tygodnia). Zderzyliśmy dane o ruchu rowerowym z pogodą, co w efekcie pozwoliło dojść do wniosku (chyba mało zaskakującego), że jak jest cieplej i nie pada to jeździmy więcej.

Dzisiaj będzie o tym skąd i dokąd jeżdżą sobie rowery

Sprawdzimy też czy teza postawiona w poprzedniej części (na podstawie ruchu w poszczególnych porach dnia) o dojazdach do i z pracy jest prawdziwa. A przynajmniej zbliżymy się do jej weryfikacji.

Zaczniemy od podłączenia się do źródła danych:

SQLite_db_file <- "veturilo_2017-05-08.sqlite3"

library(dplyr)
library(ggplot2)
library(lubridate)
library(ggmap)

theme_set(theme_minimal())

# połączenie do bazy danych o rowerach
sqllite_db <- src_sqlite(SQLite_db_file)

SQLite_db_file <- "veturilo_2017-05-08.sqlite3"

library(dplyr)

library(ggplot2)

library(lubridate)

library(ggmap)

theme_set(theme_minimal())

# połączenie do bazy danych o rowerach

sqllite_db <- src_sqlite(SQLite_db_file)

Gdzie są stacje Veturilo?

Pobieramy dane o lokalizacji stacji do pamięci – nie są to duże dane, więc możemy je mieć pod ręką.

veturilo_map <- tbl(sqllite_db, "veturilo_map") %>% collect()

1	veturilo_map <- tbl(sqllite_db, "veturilo_map") %>% collect()

Od razu pobierzmy mapę Warszawy z Google Maps i zobaczmy gdzie są zlokalizowane stacje:

warsaw_map <- get_map("Warszawa, Polska", zoom = 11)
ggmap(warsaw_map) +
   geom_point(data = veturilo_map, aes(long, lat), color="red") +
   theme_void()

warsaw_map <- get_map("Warszawa, Polska", zoom = 11)

ggmap(warsaw_map) +

geom_point(data = veturilo_map, aes(long, lat), color="red") +

theme_void()

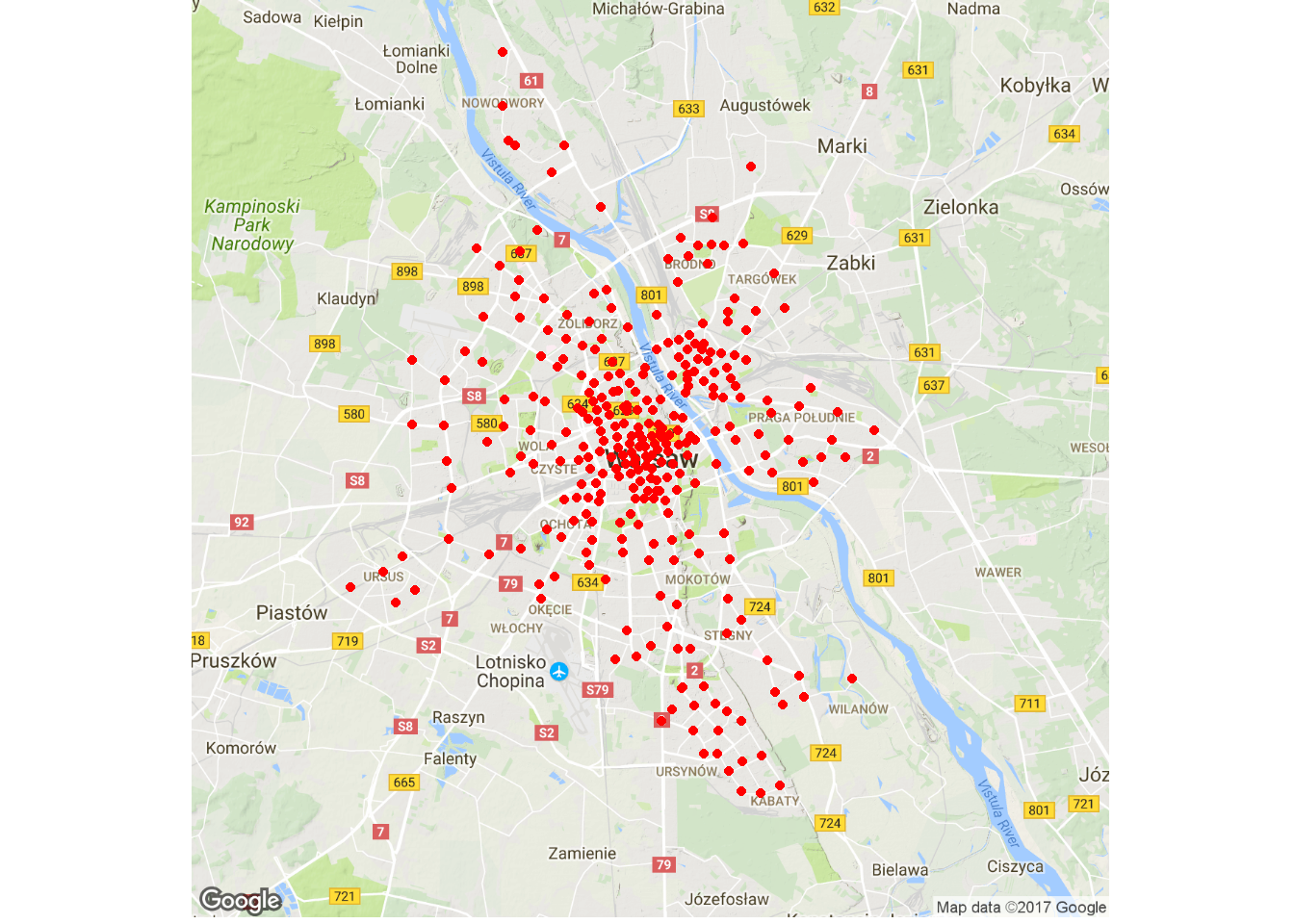
Ważne, zgodnie z komentarzem Maćka spod poprzedniej części brakuje nam informacji o stacjach sponsorskich. Bardzo żałuję, że tego nie wiedziałem. Nie mamy informacji o stacjach w pobliżu centrów handlowych (nie “galerii”, bo w gelariach to wiszą obrazy, sklepy są w centrach handlowych), a to byłyby ciekawe dane (w jakich godzinach przyjeżdżają do nich ludzie?). No trudno.

Czy rowerem dojeżdza się do i z pracy?

W poprzedniej części wysnułem wniosek, że rowery w dni robocze używane są jako sposób dotarcia do i z pracy. Ja działałbym według schematu:

z domu dojść do najbliższej stacji Veturilo
podjechać rowerem do metra
przejechać metrem kilka stacji
przy docelowej stacji metra wziąć kolejny rower
i dojechać do najbliższej pracy stacji metra

Oczywiście ma to sens, kiedy mieszkamy i pracujemy w rozsądnej odległości od stacji Veturlio. I mamy do przejechania kawałek metrem. To może się sprawdzać dla kogoś kto pracuje w okolicach ulicy Grzybowskiej (jest tutaj kilka biurowców – na przykład nowy Q22, jest stajca rowerów o numerze 9483), a mieszka na przykład na Ursynowie przy ulicy Romera (stacja 9606): rowerem z Romera do metra Stokłosy, metrem do Świętokszyskiej, rowerem z metra do stacji na rogu Grzybowskiej i al. Jana Pawła II.

Zakładając taki sposób dotarcia do pracy możemy spodziewać się widocznych zmian w ilości rowerów na stacjach Veturilo w pobliżu metra. Sprawdźmy czy tak jest.

Napierw wyznaczymy stacje przy metrze. Na szczęście mają w nazwie “Metro”, więc wybierzemy odpowiednie; potrzebne nam są jedynie numery stacji:

veturilo_metro <- veturilo_map %>%
   filter(grepl("Metro", name) == TRUE) %>%
   select(number)

veturilo_metro <- veturilo_map %>%

filter(grepl("Metro", name) == TRUE) %>%

select(number)

Teraz możemy z tabeli z pełnymi danymi wyjąć tylko te, które dotyczą stacji metra. Agregując dane do godzin w poszczególne dni tygodnia zobaczymy, że:

veturilo_data <- tbl(sqllite_db, "veturilo")

veturilo_data %>%
   select(hour, wday, number, bikes) %>%
   filter(number %in% veturilo_metro$number) %>%
   group_by(wday, hour) %>%
   summarise(n_bikes = mean(bikes)) %>%
   ungroup() %>%
   collect() %>%
   mutate(wday = factor(wday, levels=c("pn", "wt", "sr", "cz", "pt", "sb", "nd"))) %>%
   ggplot() +
   geom_line(aes(hour, n_bikes)) +
   geom_vline(xintercept = c(8, 10, 16, 18), color="lightgreen", alpha=0.6) +
   facet_wrap(~wday) +
   labs(x="Godzina", y="Średnia liczba rowerów na stacjach")

veturilo_data <- tbl(sqllite_db, "veturilo")

veturilo_data %>%

select(hour, wday, number, bikes) %>%

filter(number %in% veturilo_metro$number) %>%

group_by(wday, hour) %>%

summarise(n_bikes = mean(bikes)) %>%

ungroup() %>%

collect() %>%

mutate(wday = factor(wday, levels=c("pn", "wt", "sr", "cz", "pt", "sb", "nd"))) %>%

ggplot() +

geom_line(aes(hour, n_bikes)) +

geom_vline(xintercept = c(8, 10, 16, 18), color="lightgreen", alpha=0.6) +

facet_wrap(~wday) +

labs(x="Godzina", y="Średnia liczba rowerów na stacjach")

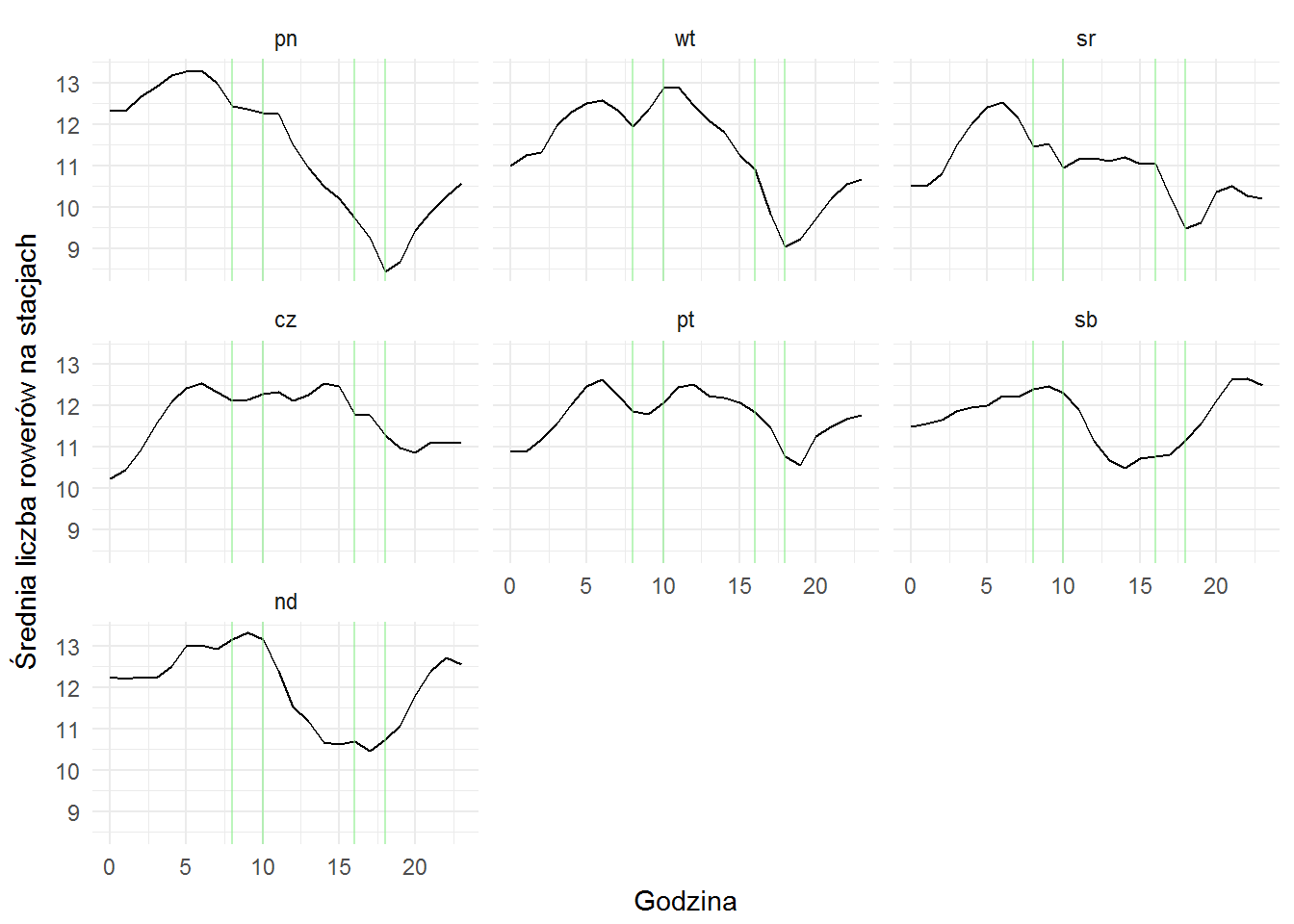
W dni robocze na stacjach koło metra średnia liczba przypiętych rowerów spada w okolicach 17-18. To mogłoby potwierdzać tezę – ludzie wychodząc z pracy wracają metrem i do domów dojeżdżają rowerami. Albo nie do domów tylko gdzieś indziej. Rano nie widać tego dołka, ale widać górki – rowerów przy stacjach metra przybywa (bo ktoś dojechał do metra i tam zostawił rower). Stosowne przeciały 8-10 i 16-18 zaznaczyłem pionowymi kreskami.

W weekendy natomiast dołek jest nieco dłuższy i zaczyna się wcześniej (po obiedzie przy Familiadzie, jak na polski dom przystało ;). Wytłumaczyć to można tym, że społeczeństwo dojeżdża sobie metrem do atrakcyjnej lokalizacji, bierze tam rower i rusza w trasę.

Spróbujmy zobaczyć na jakich stacjach te efekty widać najbardziej. Wybierzmy tylko poniedziałek i wtorek (tutaj te popołudniowe spadki są najbardziej widoczne). Dodatkowo, aby było łatwiej – dodajmy nazwy stacji zamiast ich numerów (nie mamy ich w tabeli veturilo_data, trzeba ją złączyć z veturilo_map):

veturilo_data %>%
   select(hour, wday, number, bikes) %>%
   filter(number %in% veturilo_metro$number, wday %in% c("pn", "wt")) %>%
   group_by(number, hour) %>%
   summarise(n_bikes = mean(bikes)) %>%
   ungroup() %>%
   collect() %>%
   inner_join(veturilo_map, by="number") %>%
   ggplot() +
   geom_line(aes(hour, n_bikes)) +
   geom_vline(xintercept = c(8, 10, 16, 18), color="lightgreen", alpha=0.6) +
   facet_wrap(~name) +
   labs(x="Godzina", y="Średnia liczba rowerów na stacjach")

veturilo_data %>%

select(hour, wday, number, bikes) %>%

filter(number %in% veturilo_metro$number, wday %in% c("pn", "wt")) %>%

group_by(number, hour) %>%

summarise(n_bikes = mean(bikes)) %>%

ungroup() %>%

collect() %>%

inner_join(veturilo_map, by="number") %>%

ggplot() +

geom_line(aes(hour, n_bikes)) +

geom_vline(xintercept = c(8, 10, 16, 18), color="lightgreen", alpha=0.6) +

facet_wrap(~name) +

labs(x="Godzina", y="Średnia liczba rowerów na stacjach")

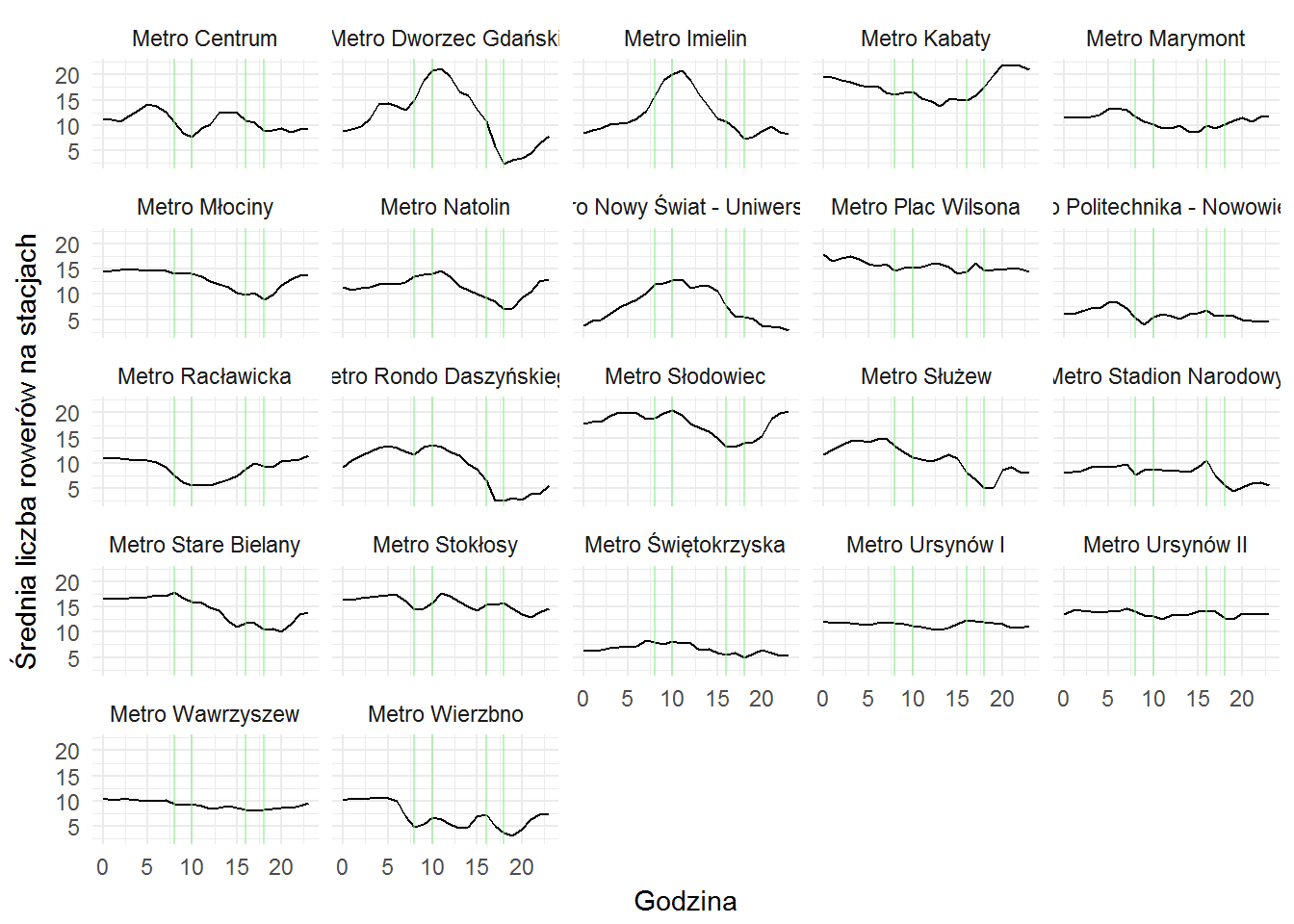
Popołudniowy spadek widać szczególnie na stacjach Dworzec Gdański, Służew, Słodowiec, Stadion Narodowy oraz Rondo Daszyńskiego. Czy to jest dowód potwierdzający moją tezę?

Mam wrażenie, że to jednak cherry picking… ale lepszej tezy nie mam na podorędziu :)

Zobaczmy jeszcze z ciekawości to samo w weekendy:

veturilo_data %>%
   select(hour, wday, number, bikes) %>%
   filter(number %in% veturilo_metro$number, wday %in% c("sb", "nd")) %>%
   group_by(number, hour) %>%
   summarise(n_bikes = mean(bikes)) %>%
   ungroup() %>%
   collect() %>%
   inner_join(veturilo_map, by="number") %>%
   ggplot() +
   geom_line(aes(hour, n_bikes)) +
   facet_wrap(~name) +
   labs(x="Godzina", y="Średnia liczba rowerów na stacjach")

veturilo_data %>%

select(hour, wday, number, bikes) %>%

filter(number %in% veturilo_metro$number, wday %in% c("sb", "nd")) %>%

group_by(number, hour) %>%

summarise(n_bikes = mean(bikes)) %>%

ungroup() %>%

collect() %>%

inner_join(veturilo_map, by="number") %>%

ggplot() +

geom_line(aes(hour, n_bikes)) +

facet_wrap(~name) +

labs(x="Godzina", y="Średnia liczba rowerów na stacjach")

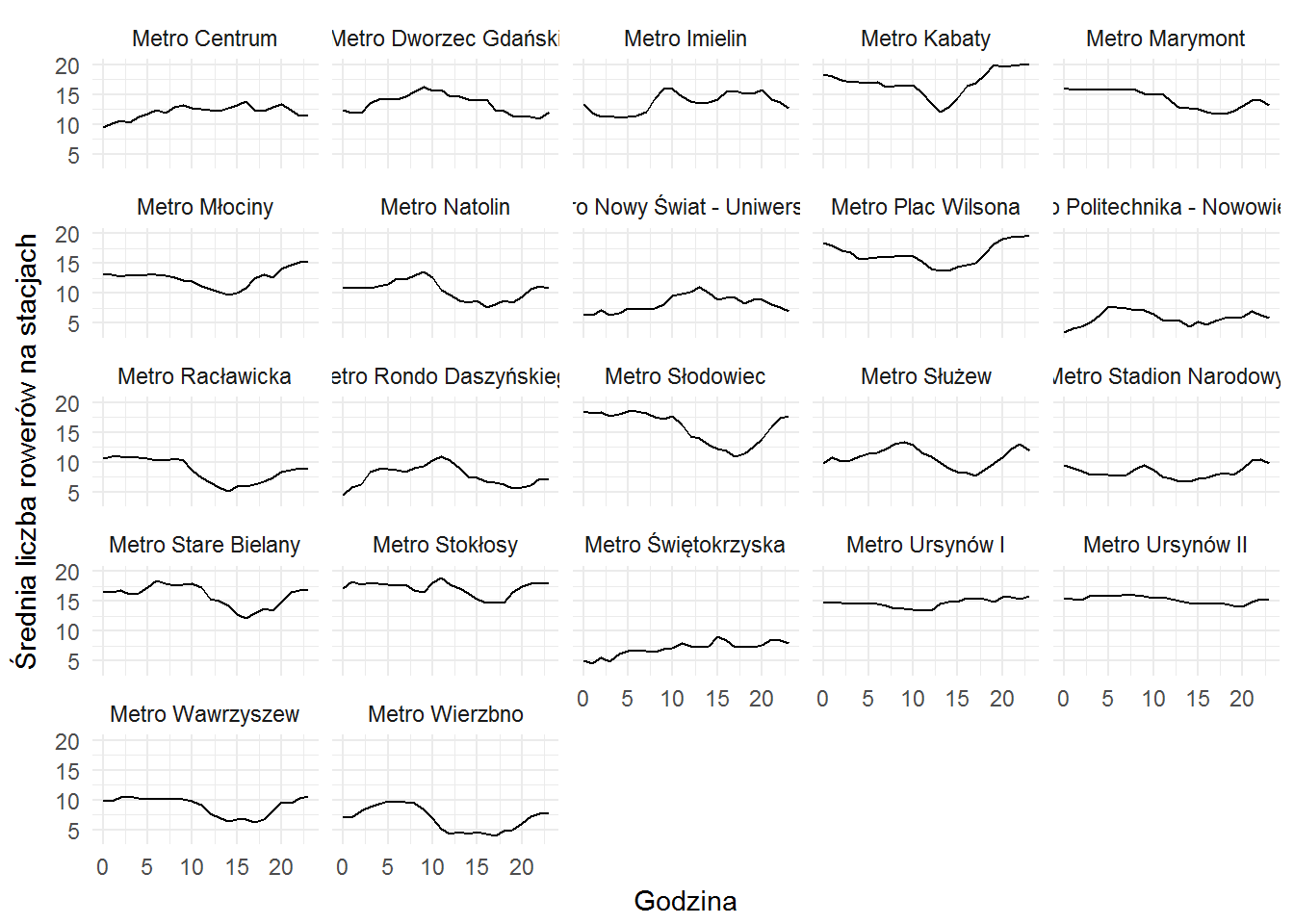
Popularne weekendowe miejsca to Kabaty, Natolin, Plac Wilsona, Słodowiec, Bielany i Wierzbno. Wiecie dlaczego? Bo niedaleko są duże parki i lasy, po których można przyjemnie pojeździć rowerem. Chyba, że to znowu cherry picking ;).

Najpopularniejsze trasy rowerowe

Czy to wybieranie danych pod tezę (jeśli jeszcze nie sprawdziliście co to cherry picking to jest to właśnie to) czy też fakt możemy sprawdzić w inny sposób. Na przykład badając skąd dokąd (z której do krótej stacji) jeżdżą rowery.

Mamy do tego przygotowaną tabelę bikes, w której znajdują się tylko trzy informacje (ale za to jest ich bardzo dużo) – timestamp (czyli godzina i data pobrania informacji), numer roweru i numer stacji na której rower był przypięty w danej chwili. To są informacje o rowerach na stacjach – rowery w ruchu “nie istnieją” w bazie w danej chwili. Skąd są te informacje?

W danych z Veturilo mamy dla każdej stacji listę przypiętych do niej rowerów (jako jedno pole, numery rowerów rozdzielone przecinkami). Wystarczy wyłuskać te numery do osobnych kolumn (na przykład używając separate() z pakietu tidyr), a później z-melt-ować (melt() z reshape2) albo zrobić im gather() (z tidyr). Ja te wszystkie operacje przeprowadziłem i ich wynik mam w tabeli “bikes” w SQLite’owej sqllite_db.

bikes <- tbl(sqllite_db, "bikes")

1	bikes <- tbl(sqllite_db, "bikes")

Początek tabeli wygląda tak:

timestamp	station_number	bike_number
1489189543	9402	24892
1489189543	9403	24809
1489189543	9404	24979
1489189543	9405	24939
1489189543	9406	24561
1489189543	9407	24861

Jednocześnie możemy sprawdzić ile tak na prawdę jest rowerów – wystaczy policzyć unikalne numery:

n_bikes <- bikes %>% select(bike_number) %>% distinct() %>% collect() %>% nrow()

1	n_bikes <- bikes %>% select(bike_number) %>% distinct() %>% collect() %>% nrow()

Jak widać unikalnych rowerów mamy 4013 Ograniczenie ich liczby w poprzednim wpisie poprzez średnią i odchylenie standardowe dało o około 400 mniej, na co zwrócił uwagę Maciek w komentarzu.

Przy okazji ciekawostka – union() wbudowane w R nie zadziała na danych trzymanych w tabeli “na serwerze” (SQLite, mySQL). A to dlatego, że serwer SQL nie rozumie funkcji unique. Ale rozumie distinct, a pakiet dplyr takową posiada (w dodatku według dokumentacji jest szybsza). Cóż – trzeba się przestawić na inną funkcję, robiącą to samo…

Niestety nie każda funkcja która działa w przypadku tabel trzymanych w pamięci działa na serwerach (na przykład przydałyby się nam funckje lag lub lead – przesuwające dane w tabeli o zadaną ilość rzędów). Ale można sobie poradzić, przynajmniej spróbujemy. A tutaj lag() bardzo by się przydało – potrzebujemy przesunąć o jeden wiersz dane dla każdego z rowerów. Tak, żeby otrzymać informację o obecnej i poprzedniej stacji, do której rower jest przypięty.

Dygresja – pokazuję i objaśniam

Dla uproszczenia przykład (“Nic nie działa na wyobraźnię tak, jak dobry przykład” – rzekomo to słowa Lenina, ale nie znajduję potwierdzenia w Google), który wyjaśni co trzeba zrobić. Jeśli nie chcesz zrozumieć na czym polega trick – kliknij tutaj i przejdź dalej.

Zbudujmy sobie tabelkę z przykładowymi danymi:

set.seed(12345) # żeby wyniki były powtarzalne

df <- data.frame(czas_o = sample(1:20),
                 stacja_o = sample(c("A", "B", "C", "D"), size = 20, replace = T),
                 rower = sample(c("R1", "R2", "R3"), size = 20, replace = T))

set.seed(12345) # żeby wyniki były powtarzalne

df <- data.frame(czas_o = sample(1:20),

stacja_o = sample(c("A", "B", "C", "D"), size = 20, replace = T),

rower = sample(c("R1", "R2", "R3"), size = 20, replace = T))

czas_o	stacja_o	rower
15	B	R3
17	B	R2
14	D	R3
16	C	R3
8	C	R1
3	B	R1
5	C	R1
7	C	R1
9	A	R1
11	B	R2
1	D	R3
2	A	R3
6	A	R1
10	C	R1
20	B	R3
19	B	R2
12	D	R3
4	D	R1
13	C	R2
18	A	R1

Teraz sortując po czasie i grupując po numerze roweru – przesuńmy dane o czasie i stacji jeden wiersz w górę:

df2 <- df %>%
   group_by(rower) %>%
   arrange(czas_o) %>%
   mutate(stacja_p = lead(stacja_o), czas_p = lead(czas_o)) %>%
   ungroup() %>%
   select(rower, czas_o, czas_p, stacja_o, stacja_p) %>%
   arrange(rower, czas_o)

df2 <- df %>%

group_by(rower) %>%

arrange(czas_o) %>%

mutate(stacja_p = lead(stacja_o), czas_p = lead(czas_o)) %>%

ungroup() %>%

select(rower, czas_o, czas_p, stacja_o, stacja_p) %>%

arrange(rower, czas_o)

rower	czas_o	czas_p	stacja_o	stacja_p
R1	3	4	B	D
R1	4	5	D	C
R1	5	6	C	A
R1	6	7	A	C
R1	7	8	C	C
R1	8	9	C	A
R1	9	10	A	C
R1	10	18	C	A
R1	18	NA	A	NA
R2	11	13	B	C
R2	13	17	C	B
R2	17	19	B	B
R2	19	NA	B	NA
R3	1	2	D	A
R3	2	12	A	D
R3	12	14	D	D
R3	14	15	D	B
R3	15	16	B	C
R3	16	20	C	B
R3	20	NA	B	NA

Wynik to tabela z przesuniętymi czasami i stacjami – czas_p oraz stacja_p to przesunięte położenie (czasowe i przestrzenne, że się tak wyrażę) danego roweru. I tak widzimy, że rower R1 przebył drogę z B do D pomiędzy chwilą 3 a 4. Później z D pojechał na C w czasie od 4 do 5. Z 5 do 6 – z C do A. I tak dalej. Pomiędzy chwilą 7 a 8 stał na stacji C. Na koniec, po chwili 18 gdzieś sobie odjechał ze stacji A i jeszcze nigdzie się nie zameldował. Analogicznie jest dla innych rowerów. Prześledźcie to proszę.

Możemy policzyć teraz ile rowerów przejechało ze stacji do innej stacji. Na początku pozbędziemy się informacji o rowerach, które nie wróciły i które stały na tej samej stacji:

df3 <- df2 %>% filter(!is.na(stacja_p), stacja_o != stacja_p)

1	df3 <- df2 %>% filter(!is.na(stacja_p), stacja_o != stacja_p)

rower	czas_o	czas_p	stacja_o	stacja_p
R1	3	4	B	D
R1	4	5	D	C
R1	5	6	C	A
R1	6	7	A	C
R1	8	9	C	A
R1	9	10	A	C
R1	10	18	C	A
R2	11	13	B	C
R2	13	17	C	B
R3	1	2	D	A
R3	2	12	A	D
R3	14	15	D	B
R3	15	16	B	C
R3	16	20	C	B

Teraz zobaczmy jak wygląda ruch – jakie trasy są najpopularniejsze? Z której na którą stację przejeżdża najwięcej rowerów?

df4 <- df3 %>% count(stacja_o, stacja_p) %>% arrange(desc(n), stacja_o, stacja_p)

1	df4 <- df3 %>% count(stacja_o, stacja_p) %>% arrange(desc(n), stacja_o, stacja_p)

stacja_o	stacja_p	n
C	A	3
A	C	2
B	C	2
C	B	2
A	D	1
B	D	1
D	A	1
D	B	1
D	C	1

Teraz popatrzmy – 3 przejazdy to trasa C do A. I to się zgadza – porównując z drugą tabelką z naszego przykładu:

R1 w 5 do 6
R1 w 8 do 9
R1 w 10 do 18

A na przykład B do C:

R2 w 11 do 13
R3 w 15 do 16

Koniec przykładu

Dokładnie to samo trzeba zrobić z rowerami (już nie tymi przykładowymi) – kod jest analogiczny. Ponieważ danych jest bardzo dużo obrobiłem je na boku. Grupowanie w ramach tabeli sprawia, że kolejne operacje przeprowadzane są na grupach, a nie na całości (na przykład średnia liczona jest w ramach grupy, a nie wszystkich danych). Ten sam efekt da wyjęcie grupy do osobnej tabeli, przeprowadzenie obliczeń i dołączenie kolejnych podzbiorów (grup) do nowej tabeli. Tak też zrobiłem, wyniki zapisując w pliku RDS. Potrzeba matką wynalazków. Jednak jeśli masz dużo pamięci w komputerze poniższy kod powinien zadziałać:

bikes_local <- bikes %>%
   group_by(bike_number) %>%
   arrange(timestamp) %>%
   collect(n=Inf) %>%
   mutate(station_number_p = lead(station_number),
          timestamp_p = lead(timestamp)) %>%
   ungroup() %>%
   select(bike_number, timestamp, timestamp_p, station_number, station_number_p) %>%
   filter(!is.na(station_number_p), station_number != station_number_p)

bikes_local <- bikes %>%

group_by(bike_number) %>%

arrange(timestamp) %>%

collect(n=Inf) %>%

mutate(station_number_p = lead(station_number),

timestamp_p = lead(timestamp)) %>%

ungroup() %>%

select(bike_number, timestamp, timestamp_p, station_number, station_number_p) %>%

filter(!is.na(station_number_p), station_number != station_number_p)

Z około 49 milionów wierszy zrobiło się 630 tysięcy. Zobaczmy jak wygląda ruch pomiędzy stacjami. Numery stacji nie są ciągłe od jedynki, są pomiędzy 9400 i 9716, a powyżej mamy trzy stacje z numerami w okolicach 95000 – dlatego na poniższym obrazku odrzucamy te trzy odstające stacje, dodatkowo logarytmujemy liczbę przejazdów, żeby zaakcentować różnice kolorami:

bikes_local %>%
   filter(station_number < 9720, station_number_p < 9720) %>%
   count(station_number, station_number_p) %>%
   ggplot() +
   geom_tile(aes(station_number, station_number_p, fill=log10(n))) +
   scale_fill_gradient(low="yellow", high="red") +
   labs(x="Stacja A", y="Stacja B", fill="Log10 z liczby rowerów\nprzejeżdżających z A do B")

bikes_local %>%

filter(station_number < 9720, station_number_p < 9720) %>%

count(station_number, station_number_p) %>%

ggplot() +

geom_tile(aes(station_number, station_number_p, fill=log10(n))) +

scale_fill_gradient(low="yellow", high="red") +

labs(x="Stacja A", y="Stacja B", fill="Log10 z liczby rowerów\nprzejeżdżających z A do B")

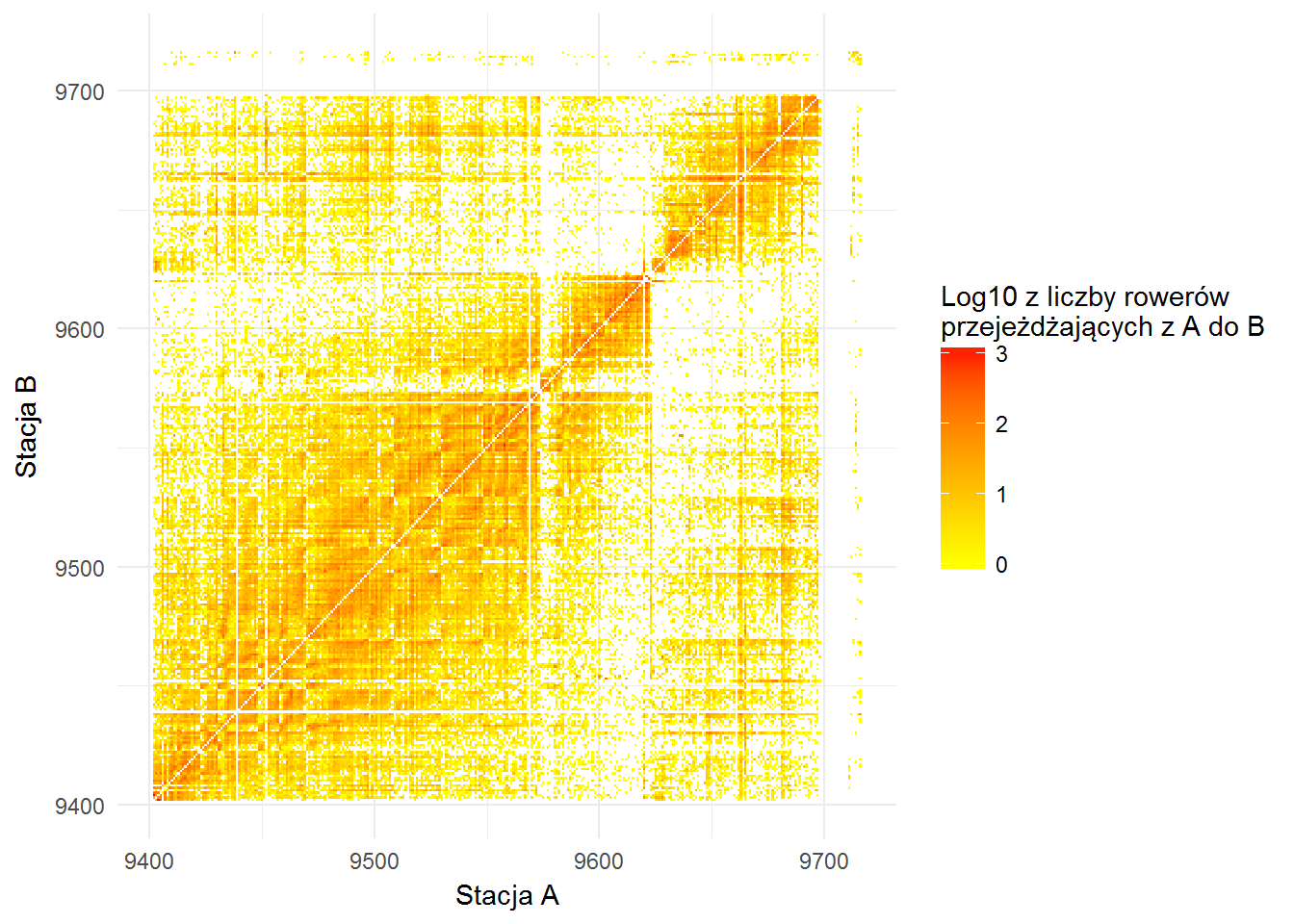
Ładnie to wygląda, niewiele mówi. Coś jednak – najczęstrze podróże są w ramach stacji o sąsiednich numerach (pierwsza dwudziestka “tras”, już bez wyłączenia stacji o dużych numerach, za to z zamianą numerów na nazwy stacji) wygląda następująco:

bikes_local %>%
   count(station_number, station_number_p) %>%
   ungroup() %>%
   inner_join(veturilo_map[,c(1,5)], by=c("station_number"="number")) %>%
   inner_join(veturilo_map[,c(1,5)], by=c("station_number_p"="number")) %>%
   select(StacjaA=name.x, StacjaB=name.y, Liczba=n) %>%
   top_n(n=20, wt=Liczba) %>%
   arrange(desc(Liczba))

bikes_local %>%

count(station_number, station_number_p) %>%

ungroup() %>%

inner_join(veturilo_map[,c(1,5)], by=c("station_number"="number")) %>%

inner_join(veturilo_map[,c(1,5)], by=c("station_number_p"="number")) %>%

select(StacjaA=name.x, StacjaB=name.y, Liczba=n) %>%

top_n(n=20, wt=Liczba) %>%

arrange(desc(Liczba))

StacjaA	StacjaB	Liczba
Marymoncka – Dewajtis	Dewajtis – UKSW	1242
Dewajtis – UKSW	Marymoncka – Dewajtis	1232
al. Niepodległości – Batorego	Stefana Banacha – UW	997
Stefana Banacha – UW	al. Niepodległości – Batorego	979
Lipowa – Dobra 2	Lipowa – Dobra	907
Lipowa – Dobra	Lipowa – Dobra 2	772
Jastrzębowskiego – SGGW	Metro Ursynów I	635
Pileckiego – Alternatywy	Metro Imielin	633
Metro Imielin	Pileckiego – Alternatywy	625
Metro Ursynów I	Jastrzębowskiego – SGGW	592
Plac Hallera – Dąbrowszczaków	Plac Wileński	572
Rosoła – Ciszewskiego – SGGW	Jastrzębowskiego – SGGW	537
Metro Natolin	Metro Kabaty	508
Jastrzębowskiego – SGGW	Rosoła – Ciszewskiego – SGGW	492
Metro Kabaty	Stryjeńskich – Wąwozowa	466
Plac Wileński	Plac Hallera – Dąbrowszczaków	458
Dworzec Wschodni – Kijowska	Pętla Kawęczyńska-Bazylika	454
Metro Kabaty	Metro Natolin	445
Stryjeńskich – Belgradzka	Metro Natolin	441
Wybrzeże Szczecińskie – Stadion Narodowy	Rondo Waszyngtona – Stadion Narodowy	431

Takie zestawienia świetnie nadają się do prezentacji w formie grafu, w dodatku skierowanego (takiego, gdzie kierunek przepływu ma znaczenie). Ograniczymy jego rozmiary do par stacji pomiędzy którymi było co najmniej 100 przejazdów. Najpierw przygotujemy graf:

library(igraph)

network_links_full <- bikes_local %>%
   count(station_number, station_number_p) %>%
   ungroup() %>%
   inner_join(veturilo_map[,c(1,5)], by=c("station_number"="number")) %>%
   inner_join(veturilo_map[,c(1,5)], by=c("station_number_p"="number")) %>%
   select(StacjaA=name.x, StacjaB=name.y, Liczba=n)

# ograniczenie wierzchołków na potrzeby grafu
network_links <- filter(network_links_full, Liczba >= 100)

# za pomocą igraph zrobimy graf
g <- graph_from_data_frame(network_links, directed = TRUE)

library(igraph)

network_links_full <- bikes_local %>%

count(station_number, station_number_p) %>%

ungroup() %>%

inner_join(veturilo_map[,c(1,5)], by=c("station_number"="number")) %>%

inner_join(veturilo_map[,c(1,5)], by=c("station_number_p"="number")) %>%

select(StacjaA=name.x, StacjaB=name.y, Liczba=n)

# ograniczenie wierzchołków na potrzeby grafu

network_links <- filter(network_links_full, Liczba >= 100)

# za pomocą igraph zrobimy graf

g <- graph_from_data_frame(network_links, directed = TRUE)

Z takim grafem już można się fajnie pobawić. Grupowanie (automatyczne, według jakiegoś tam algorytmu) wierzchołków dało ciekawe efekty:

# przypisanie wierzchołków grafu do grup
wc <- cluster_walktrap(g, weights = E(g)$Liczba)
members <- membership(wc)

# narysujmy nasz graf
plot(g,
     vertex.size = 4, vertex.color = members,
     vertex.label.cex = 0.5, vertex.label.color = members,
     edge.arrow.size = 0, edge.curved = TRUE,
     edge.width = 2*E(g)$Liczba/mean(E(g)$Liczba))

# przypisanie wierzchołków grafu do grup

wc <- cluster_walktrap(g, weights = E(g)$Liczba)

members <- membership(wc)

# narysujmy nasz graf

plot(g,

vertex.size = 4, vertex.color = members,

vertex.label.cex = 0.5, vertex.label.color = members,

edge.arrow.size = 0, edge.curved = TRUE,

edge.width = 2*E(g)$Liczba/mean(E(g)$Liczba))

Na powyższym obrazku niewiele widać, ale można zastosować pewną sztuczkę. Otóż przygotować odpowiedni layout dla grafu na podstawie współrzędnych stacji. Piękna infografika wówczas wyjdzie. Nie trzeba jednak do tego narzędzi związanych z grafami – wystarczy *ggplot**:

network_map <- network_links_full %>%
   inner_join(veturilo_map[,3:5], by=c("StacjaA"="name")) %>%
   rename(LongA=long, LatA=lat) %>%
   inner_join(veturilo_map[,3:5], by=c("StacjaB"="name")) %>%
   rename(LongB=long, LatB=lat)

ggmap(warsaw_map, darken = 0.6) +
   geom_segment(data=filter(network_map, Liczba >= 10), 
                aes(x=LongA, y=LatA, xend=LongB, yend=LatB, alpha=Liczba),
                size=1, color="white") +
   scale_alpha_continuous(range = c(0.01, 0.1)) +
   theme_void()

network_map <- network_links_full %>%

inner_join(veturilo_map[,3:5], by=c("StacjaA"="name")) %>%

rename(LongA=long, LatA=lat) %>%

inner_join(veturilo_map[,3:5], by=c("StacjaB"="name")) %>%

rename(LongB=long, LatB=lat)

ggmap(warsaw_map, darken = 0.6) +

geom_segment(data=filter(network_map, Liczba >= 10),

aes(x=LongA, y=LatA, xend=LongB, yend=LatB, alpha=Liczba),

size=1, color="white") +

scale_alpha_continuous(range = c(0.01, 0.1)) +

theme_void()

Wracając jeszcze go grafu – można przejrzeć dokładnie wynik przypisania wierzchołków (stacji Veturilo) do grup (lista wc). Na przykład skład pierwszej grupy to:

wc[[1]]

##  [1] "Dworzec Wschodni - Lubelska"              
##  [2] "Smolna - PKP Powiśle"                     
##  [3] "Okrzei - Panieńska"                       
##  [4] "Metro Stadion Narodowy"                   
##  [5] "al. Zieleniecka - Teatr Powszechny"       
##  [6] "Grochowska - Mińska"                      
##  [7] "Praga-Południe-Ratusz"                    
##  [8] "Wybrzeże Szczecińskie - Stadion Narodowy" 
##  [9] "Rondo Waszyngtona - Stadion Narodowy"     
## [10] "Waszyngtona - Kinowa"                     
## [11] "Rondo Wiatraczna"                         
## [12] "Francuska - Walecznych"                   
## [13] "Międzynarodowa - Walecznych"              
## [14] "Plac Szembeka"                            
## [15] "Pętla Gocławek"                           
## [16] "al. Stanów Zjednoczonych - Międzynarodowa"
## [17] "al. Jerozolimskie - rejon Rotundy"        
## [18] "Brukselska - PROM"

wc[[1]]

## [1] "Dworzec Wschodni - Lubelska"

## [2] "Smolna - PKP Powiśle"

## [3] "Okrzei - Panieńska"

## [4] "Metro Stadion Narodowy"

## [5] "al. Zieleniecka - Teatr Powszechny"

## [6] "Grochowska - Mińska"

## [7] "Praga-Południe-Ratusz"

## [8] "Wybrzeże Szczecińskie - Stadion Narodowy"

## [9] "Rondo Waszyngtona - Stadion Narodowy"

## [10] "Waszyngtona - Kinowa"

## [11] "Rondo Wiatraczna"

## [12] "Francuska - Walecznych"

## [13] "Międzynarodowa - Walecznych"

## [14] "Plac Szembeka"

## [15] "Pętla Gocławek"

## [16] "al. Stanów Zjednoczonych - Międzynarodowa"

## [17] "al. Jerozolimskie - rejon Rotundy"

## [18] "Brukselska - PROM"

Jak widać są to punkty w dość zwartym rejonie. Nic dziwnego – mało kto jedzie z jednego końca miasta na drugi.

Chociaż trafi się dłuższa wycieczka – na przykład z Placu Bankowego na wschodną stronę Mostu Północnego (znaczy Skłodowskiej-Curie, jak on się tam formalnie nazywa). Najdłuższa trasa jest pomiędzy stacjami Aluzyjna-Trąby (stacja 9624) a Belgradzka-Rosoła (9618) – jakieś 27 kilometrów. W zakresie za jaki mamy dane przejechały ją 2 rowery (ruszające z Aluzyjnej), co więcej oba w tym samym czasie 31 marca pomiędzy 21:15 a 21:35. Nie zrobił tego człowiek jak sądzę. Musiałby jechać ze średnią prędkością 81 km/h.

Zrobimy coś fajniejszego – wersję interaktywną. Użyjemy biblioteki D3.js, pośrednio przez pakiet networkD3.

library(networkD3)

# zmiana grafu na obiekt D3
g_d3 <- igraph_to_networkD3(g, group = members)

# zbudowanie palety kolorów
# im bardziej żółte tym większy ruch pomiędzy stacjami
cols <- g_d3$links$value
cols <- (cols - min(cols)) / (max(cols) - min(cols))
cols <- 1+round(12*log(1+cols))
pal <- RColorBrewer::brewer.pal(9, "YlOrRd")[10-cols]

# przeskalowanie gałęzi grafu
# im grubsza gałąź tym większy ruch
g_d3$links$value <- round(g_d3$links$value / 10, 2)

# przygotowanie interaktywnego grafu
forceNetwork(Links = g_d3$links, Nodes = g_d3$nodes, 
             Source = 'source', Target = 'target', 
             NodeID = 'name', Group = 'group',
             Value = 'value', linkColour = pal,
             opacity = 0.9, zoom = TRUE, 
             fontSize = 15, fontFamily = "sans-serif", 
             height = 500, width = 500)

library(networkD3)

# zmiana grafu na obiekt D3

g_d3 <- igraph_to_networkD3(g, group = members)

# zbudowanie palety kolorów

# im bardziej żółte tym większy ruch pomiędzy stacjami

cols <- g_d3$links$value

cols <- (cols - min(cols)) / (max(cols) - min(cols))

cols <- 1+round(12*log(1+cols))

pal <- RColorBrewer::brewer.pal(9, "YlOrRd")[10-cols]

# przeskalowanie gałęzi grafu

# im grubsza gałąź tym większy ruch

g_d3$links$value <- round(g_d3$links$value / 10, 2)

# przygotowanie interaktywnego grafu

forceNetwork(Links = g_d3$links, Nodes = g_d3$nodes,

Source = 'source', Target = 'target',

NodeID = 'name', Group = 'group',

Value = 'value', linkColour = pal,

opacity = 0.9, zoom = TRUE,

fontSize = 15, fontFamily = "sans-serif",

height = 500, width = 500)

Można powiększać, klikać, przeciągać. Polecam zabawę. Im grubsza gałąź tym większy ruch, podobnie z kolorem – im bardziej żółte tym większa popularność trasy.

<br />

Średni czas trwania przejazdu pomiędzy stacjami

Teraz sprawdźmy jak wyglądają czasy przejazdu pomiędzy stacjami.

W tabeli bikes_local mamy nadal dwie kolumny z czasem przypięcia danego roweru na stacji wyjściowej i końcowej – na tej podstawie możemy policzyć ile czasu trwała podróż. A właściwie to wypożyczenie roweru. Sprawdźmy jak to się rozkłada dla wypożyczeń nie dłuższych niż 90 minut:

# ile trwało wypożyczenie? w minutach
bikes_local$time_diff <- abs(bikes_local$timestamp - bikes_local$timestamp_p)/60

bikes_local %>%
   filter(time_diff < 90) %>%
   ggplot() +
   geom_histogram(aes(time_diff), binwidth = 5,
                  fill="lightgreen", color="black") +
   labs(x="Długość wypożyczenia roweru", y="Liczba wypożyczeń") +
   scale_x_continuous(breaks = seq(0, 90, 10))

# ile trwało wypożyczenie? w minutach

bikes_local$time_diff <- abs(bikes_local$timestamp - bikes_local$timestamp_p)/60

bikes_local %>%

filter(time_diff < 90) %>%

ggplot() +

geom_histogram(aes(time_diff), binwidth = 5,

fill="lightgreen", color="black") +

labs(x="Długość wypożyczenia roweru", y="Liczba wypożyczeń") +

scale_x_continuous(breaks = seq(0, 90, 10))

Dominuje czas 10-20 minut. Oczywiście. Wynika to z regulaminu Veturilo i tego, że pierwsze 20 minut jest za darmo. Pełny rozkład to:

summary(bikes_local$time_diff)

##     Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
##     0.00    14.98    20.00    67.32    35.00 55660.00

summary(bikes_local$time_diff)

## Min. 1st Qu. Median Mean 3rd Qu. Max.

## 0.00 14.98 20.00 67.32 35.00 55660.00

ta nieco ponad godzina (średnia) jest zdaje się podawana w podsumowaniach rocznych Veturilo. I jest niezłym zabiegiem marketingowym tak na marginesie… Dlaczego? zastanówcie się sami.

Jak szybko jeżdżą?

Policzymy teraz średnią prędkość jazdy użytkowników Veturilo.

Jak to zrobić? Potrzebujemy czas przejazdu i odległość. Bo jak wszyscy pamiętamy z fizyki – prędkość to:

$v = \frac{s}{t}$

Odległości wyznaczymy na podstawie położenia stacji. Będą to odległości w linii prostej, dla uproszczenia. Potrzebujemy przejść wszystkie pary stacji, każdą z każdą (trochę to potrwa):

# funkcja obliczająca euklidesową odległość
calc_dist <- function(x1,y1, x2,y2) {
   return (sqrt( (x1-x2)^2 + (y1-y2)^2))
}

dist_mat <- matrix(NA, ncol = nrow(veturilo_map), nrow = nrow(veturilo_map))

for(i in 1:nrow(veturilo_map)) {
   for(j in 1:nrow(veturilo_map)) {
      dist_tmp <- calc_dist(veturilo_map[i, "long"], veturilo_map[i, "lat"],
                          veturilo_map[j, "long"], veturilo_map[j, "lat"])
      
      # odległość A->B i B->A są takie same
      dist_mat[i, j] <- dist_tmp
      dist_mat[j, i] <- dist_tmp
   }
}

# funkcja obliczająca euklidesową odległość

calc_dist <- function(x1,y1, x2,y2) {

return (sqrt( (x1-x2)^2 + (y1-y2)^2))

}

dist_mat <- matrix(NA, ncol = nrow(veturilo_map), nrow = nrow(veturilo_map))

for(i in 1:nrow(veturilo_map)) {

for(j in 1:nrow(veturilo_map)) {

dist_tmp <- calc_dist(veturilo_map[i, "long"], veturilo_map[i, "lat"],

veturilo_map[j, "long"], veturilo_map[j, "lat"])

# odległość A->B i B->A są takie same

dist_mat[i, j] <- dist_tmp

dist_mat[j, i] <- dist_tmp

}

Mamy odległości kątowe. Ale to nie są odległości w kilometrach, trzeba to przeliczyć. Jakiś czas temu sprawdzaliśmy, że według Google Maps stopień kątowy to 111 km. Tak więc po prostu przez tyle mnożymy wszystkie wartości. Dodatkowo przekształcimy macierz na ramkę danych, tak żeby później łatwiej było ją łączyć z tym co już posiadamy (czasami przejazdów).

library(reshape2)

# żeby zachować numery stacji musimy nazwać kolumny i wiersze macieży:
rownames(dist_mat) <- veturilo_map$number
colnames(dist_mat) <- veturilo_map$number

# przeliczenie na km
dist_mat <- 111 * dist_mat

dist_df <- melt(dist_mat)

library(reshape2)

# żeby zachować numery stacji musimy nazwać kolumny i wiersze macieży:

rownames(dist_mat) <- veturilo_map$number

colnames(dist_mat) <- veturilo_map$number

# przeliczenie na km

dist_mat <- 111 * dist_mat

dist_df <- melt(dist_mat)

Teraz łączymy otrzymaną bazę odległości z czasami i liczymy średnią prędkość:

velocity <- inner_join(dist_df, bikes_local[,4:6],
                       by=c("Var1"="station_number", "Var2"="station_number_p"))

# usuwamy "przejazdy" z zerowym czasem trwania
velocity <- filter(velocity, time_diff != 0)

# czas mamy w minutach - dzielimy przez 60, żeby prędkość była w km/h
velocity$velocity <- velocity$value / (velocity$time_diff / 60)

velocity <- inner_join(dist_df, bikes_local[,4:6],

by=c("Var1"="station_number", "Var2"="station_number_p"))

# usuwamy "przejazdy" z zerowym czasem trwania

velocity <- filter(velocity, time_diff != 0)

# czas mamy w minutach - dzielimy przez 60, żeby prędkość była w km/h

velocity$velocity <- velocity$value / (velocity$time_diff / 60)

Średnia prędkość przejazdu pomiędzy stacjami to 8.4 km/h. Ja z kilku pomiarów na Endomondo mam średnią w okolicach 13 km/h – te 8.4 km/h wygląda prawdopodobnie, tym że odległość liczymy w linii prostej (co pewnie zaniża ją o jakieś 10-15%), oraz przyjmujemy że każdy przejeżdza trasę od stacji do stacji, bez zbaczania i zatrzymywania się.

Rozkład prędkości wygląda następująco:

summary(velocity$velocity)

##      Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
##     0.000     4.125     6.664     8.436     9.468 15150.000

summary(velocity$velocity)

## Min. 1st Qu. Median Mean 3rd Qu. Max.

## 0.000 4.125 6.664 8.436 9.468 15150.000

velocity %>%
   filter(velocity <= 25) %>%  # zdecydowana większość przejazdów jest poniżej 25 km/h
   ggplot() +
   geom_density(aes(velocity), fill="lightgreen") +
   geom_vline(xintercept = mean(velocity$velocity)) +
   labs(x="Prędkość [km/h]", y="Gęstość prawdopodobieństwa")

velocity %>%

filter(velocity <= 25) %>% # zdecydowana większość przejazdów jest poniżej 25 km/h

ggplot() +

geom_density(aes(velocity), fill="lightgreen") +

geom_vline(xintercept = mean(velocity$velocity)) +

labs(x="Prędkość [km/h]", y="Gęstość prawdopodobieństwa")

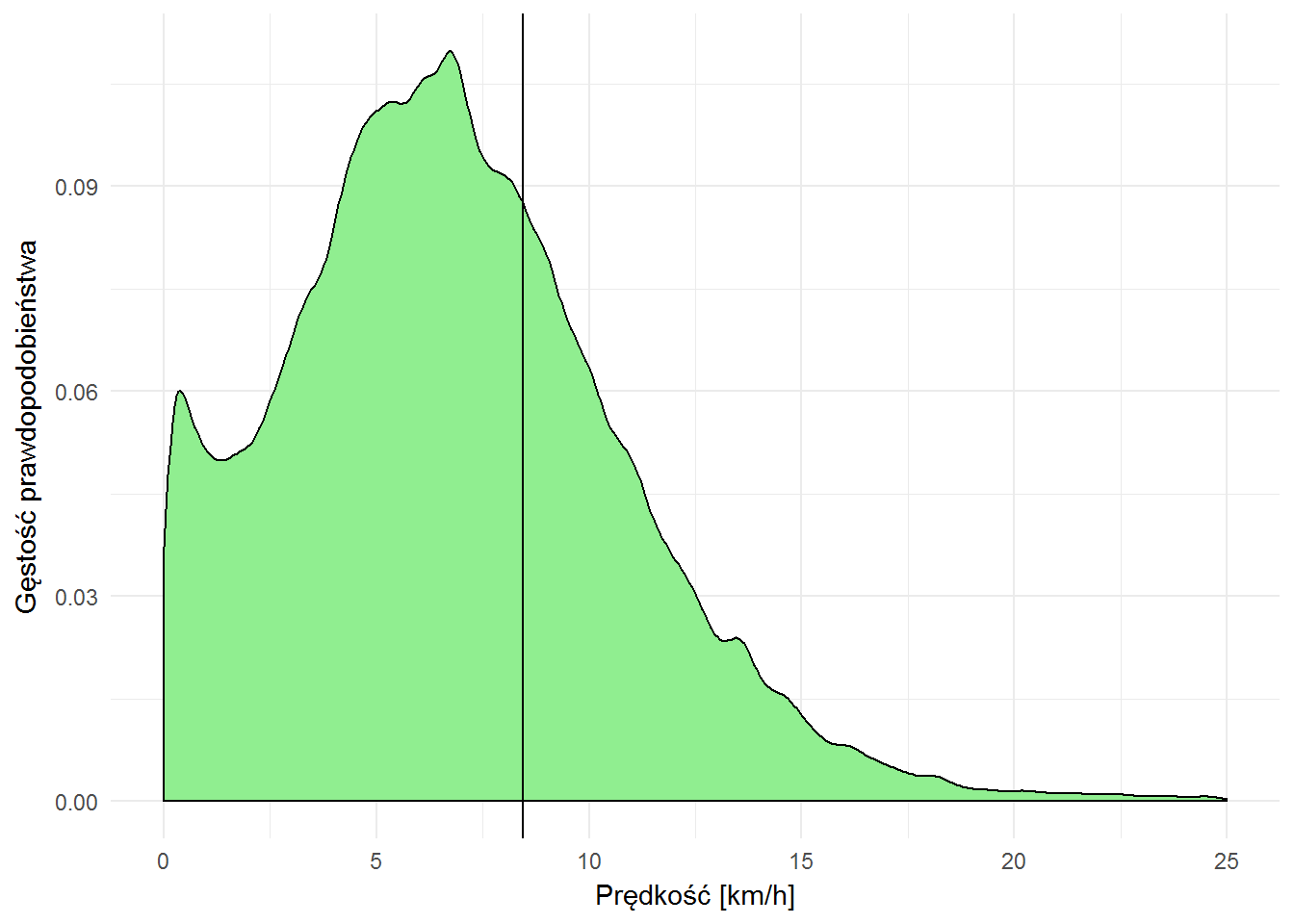
Jak to wygląda pomiędzy różnymi stacjami?

velocity %>%
   filter(velocity < 25) %>%
   filter(Var1 <= 9720, Var2 <= 9720) %>%
   group_by(Var1, Var2) %>%
   summarise(velocity = mean(velocity)) %>%
   ungroup() %>%
   ggplot() +
   geom_point(aes(Var1, Var2, color=velocity), alpha=0.2) +
   labs(x="Stacja A", y="Stacja B", color="Średnia prędkość\nprzejazdu między\nstacjami [km/h]")

velocity %>%

filter(velocity < 25) %>%

filter(Var1 <= 9720, Var2 <= 9720) %>%

group_by(Var1, Var2) %>%

summarise(velocity = mean(velocity)) %>%

ungroup() %>%

ggplot() +

geom_point(aes(Var1, Var2, color=velocity), alpha=0.2) +

labs(x="Stacja A", y="Stacja B", color="Średnia prędkość\nprzejazdu między\nstacjami [km/h]")

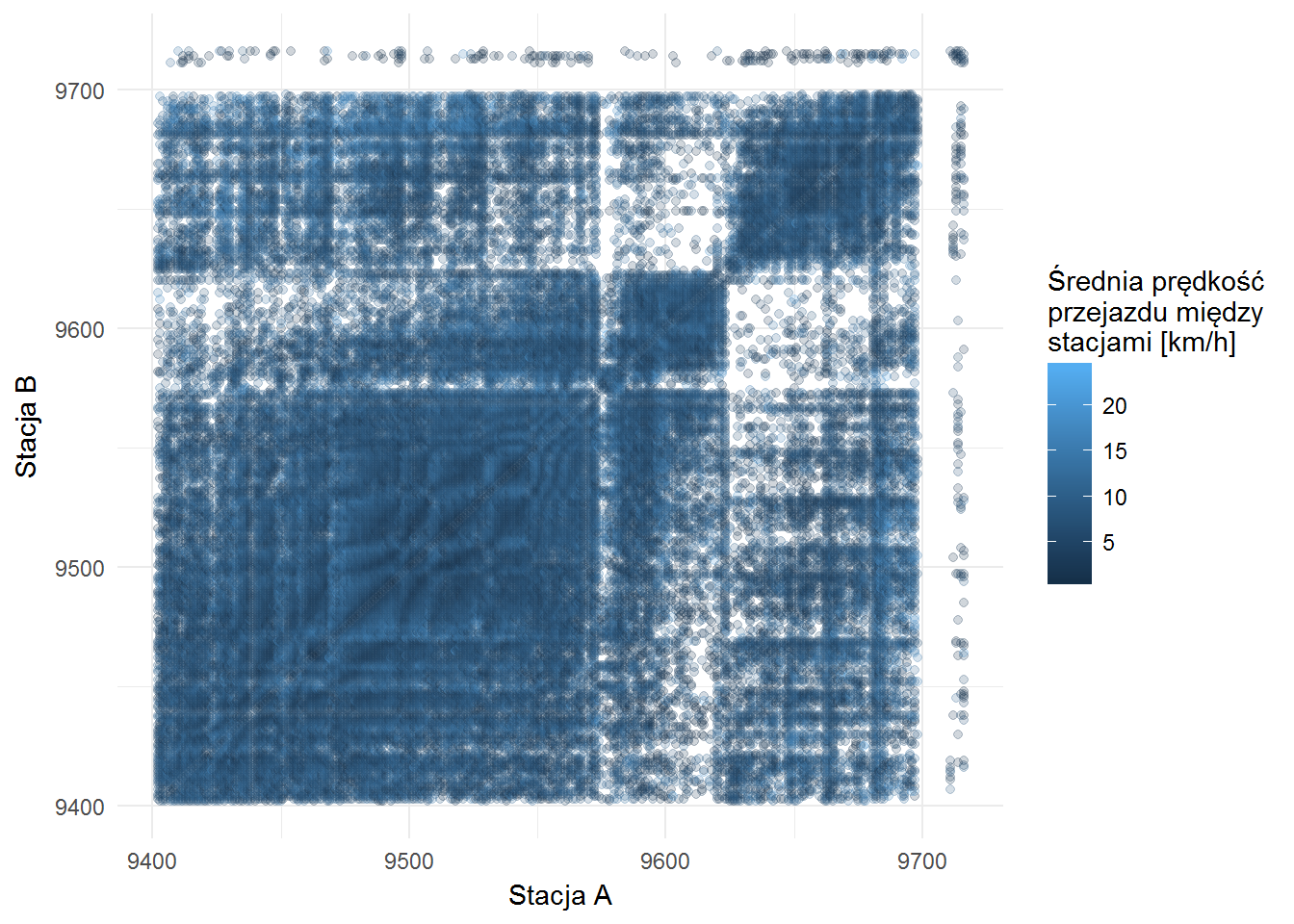
Widać, że jest to dość równomierne i trasa nie ma większego znaczenia dla prędkości.

Można spróbować zestawić średnie czasy przejazdu z warunkami atmosferycznymi (głównie temperaturą, wilgotnością i prędkością wiatru). Aby to zrobić trzeba:

zestawić dane z tabeli bikes_local z tabelą weather z poprzedniego odcinka (grupując najpierw dane po godzinach)
dodać do tego odległości między stacjami
policzyć prędkość dla przejazdów między stacjami
uśrednić prędkości według godzin
dodać warunki pogodowe

# średnie czas przejazdu między stacjami - wg godziny
bikes_by_hour <- bikes_local %>%
   select(timestamp, station_number, station_number_p, time_diff) %>%
   mutate(timestamp = as.POSIXct(timestamp, origin="1970-01-01"),
          month=month(timestamp), day=day(timestamp), hour=hour(timestamp)) %>%
   group_by(month, day, hour, station_number, station_number_p) %>%
   summarise(time_diff = mean(time_diff)) %>%
   ungroup()

# średnie warunki pogodowe - wg godziny
weather <- readRDS("pogoda.RDS")
weather_by_hour <- weather %>%
   na.omit() %>%
   mutate(month=month(time), day=day(time), hour=hour(time)) %>%
   group_by(month, day, hour) %>%
   summarise(temp=mean(temp), wiatr=mean(wiatr), wilgotnosc=mean(wilgotnosc))

# połączenie czasów przejazdów z odległościami
velocity_by_hour <- inner_join(dist_df, bikes_by_hour,
                       by=c("Var1"="station_number", "Var2"="station_number_p"))

# prędkość przejazdów
velocity_by_hour$velocity <- velocity_by_hour$value / (velocity_by_hour$time_diff / 60)

velocity_by_hour <- velocity_by_hour %>%
   group_by(month, day, hour) %>%
   summarise(velocity = mean(velocity)) %>%
   ungroup()

weather_velocity_by_hour <- inner_join(velocity_by_hour, weather_by_hour,
                               by=c("month"="month", "day"="day", "hour"="hour")) %>%
   filter(velocity <= 50)

# średnie czas przejazdu między stacjami - wg godziny

bikes_by_hour <- bikes_local %>%

select(timestamp, station_number, station_number_p, time_diff) %>%

mutate(timestamp = as.POSIXct(timestamp, origin="1970-01-01"),

month=month(timestamp), day=day(timestamp), hour=hour(timestamp)) %>%

group_by(month, day, hour, station_number, station_number_p) %>%

summarise(time_diff = mean(time_diff)) %>%

ungroup()

# średnie warunki pogodowe - wg godziny

weather <- readRDS("pogoda.RDS")

weather_by_hour <- weather %>%

na.omit() %>%

mutate(month=month(time), day=day(time), hour=hour(time)) %>%

group_by(month, day, hour) %>%

summarise(temp=mean(temp), wiatr=mean(wiatr), wilgotnosc=mean(wilgotnosc))

# połączenie czasów przejazdów z odległościami

velocity_by_hour <- inner_join(dist_df, bikes_by_hour,

by=c("Var1"="station_number", "Var2"="station_number_p"))

# prędkość przejazdów

velocity_by_hour$velocity <- velocity_by_hour$value / (velocity_by_hour$time_diff / 60)

velocity_by_hour <- velocity_by_hour %>%

group_by(month, day, hour) %>%

summarise(velocity = mean(velocity)) %>%

ungroup()

weather_velocity_by_hour <- inner_join(velocity_by_hour, weather_by_hour,

by=c("month"="month", "day"="day", "hour"="hour")) %>%

filter(velocity <= 50)

Zobaczmy co mamy i jak wygląda korelacja pomiędzy prędkością a godziną i warunkami atmosferycznymi:

library(corrgram)
corrgram(weather_velocity_by_hour[,3:7],
         lower.panel = panel.pts, upper.panel = panel.cor)

library(corrgram)

corrgram(weather_velocity_by_hour[,3:7],

lower.panel = panel.pts, upper.panel = panel.cor)

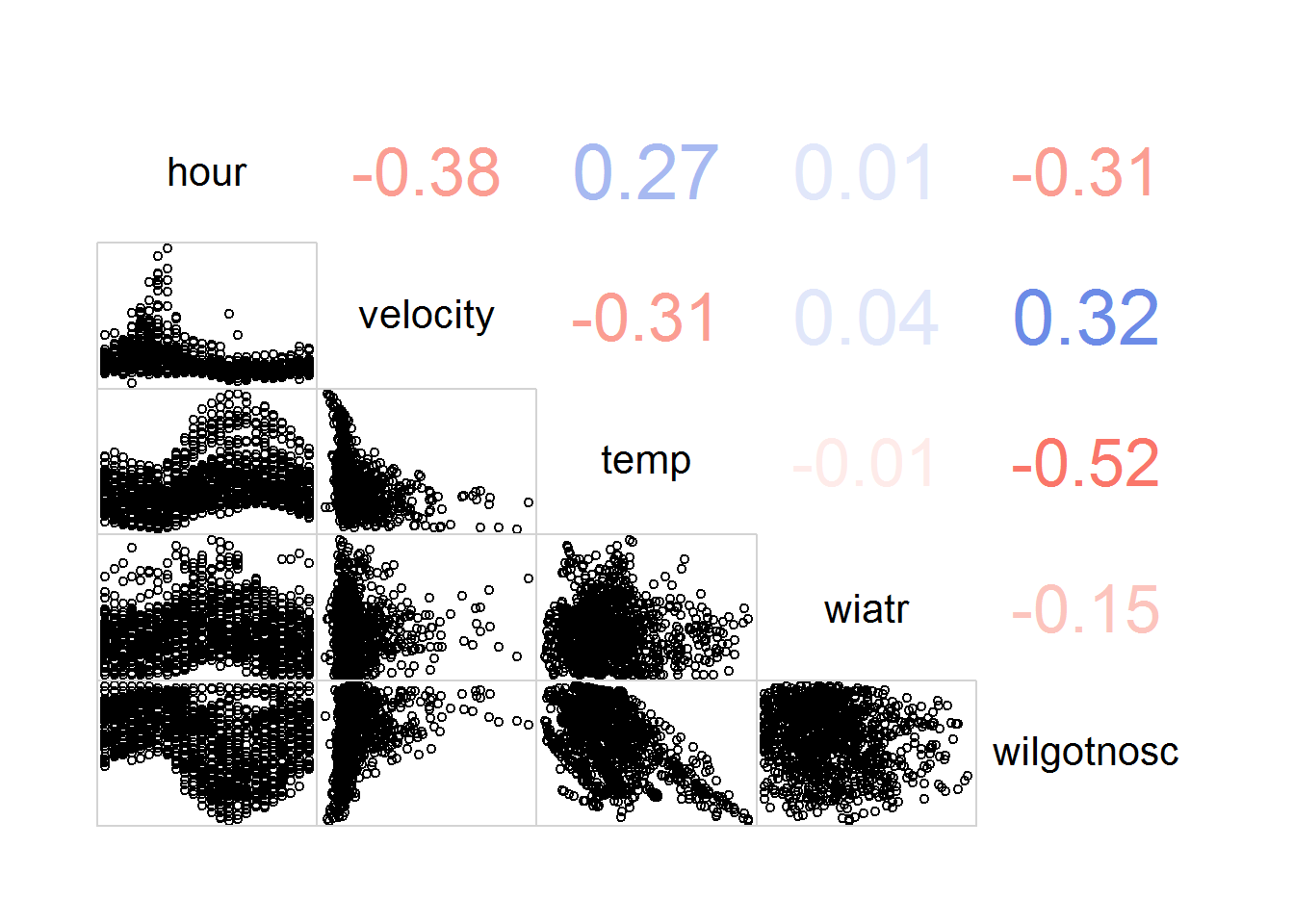
Widać słabe (mniejsze niż 0.5) korelacje prędkości – dodatnią z wilgotnością (0.32) oraz ujemną z temperaturą (-0.31). Zobaczmy to w szczegółach.

Temperatura:

ggplot(weather_velocity_by_hour) +
   geom_point(aes(temp, velocity), alpha=0.4) +
   geom_smooth(aes(temp, velocity)) +
   labs(x="Temperatura [C]", y="Średnia prędkość [km/h]")

ggplot(weather_velocity_by_hour) +

geom_point(aes(temp, velocity), alpha=0.4) +

geom_smooth(aes(temp, velocity)) +

labs(x="Temperatura [C]", y="Średnia prędkość [km/h]")

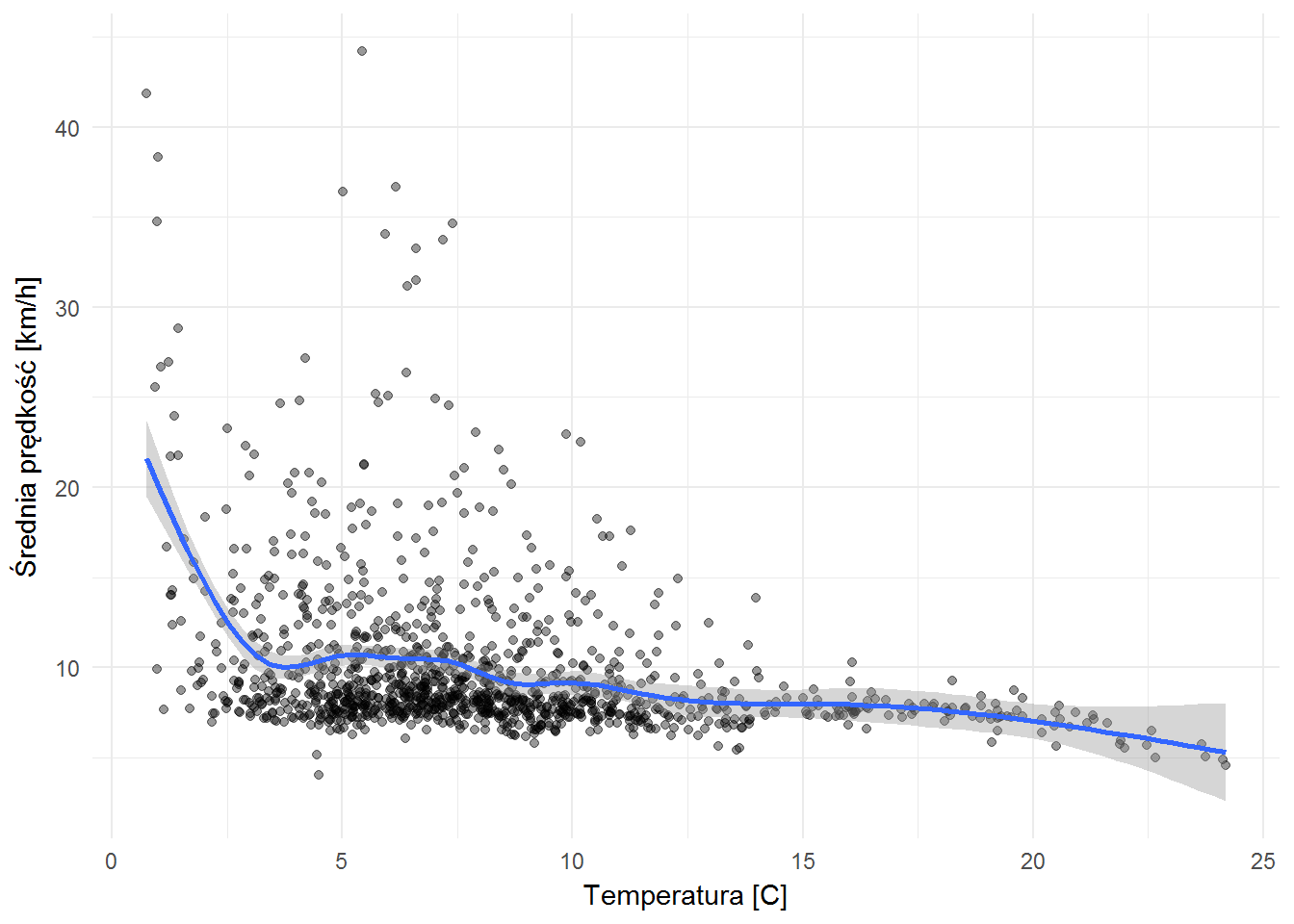
Trochę jest tak, że im zimniej tym szybciej jeżdżą. Zupełnie inaczej niż z cząsteczkami według praw termodynamiki ;) ale trzeba pamiętać, że jak na razie to temperatury nie były zbyt wysokie. Takie zestawienia można robić dla danych z całego roku.

Dla wilgotności wygląda to zaś tak:

ggplot(weather_velocity_by_hour) +
   geom_point(aes(wilgotnosc, velocity), alpha=0.4) +
   geom_smooth(aes(wilgotnosc, velocity)) +
   labs(x="Wilgotność powietrza [%]", y="Średnia prędkość [km/h]")

ggplot(weather_velocity_by_hour) +

geom_point(aes(wilgotnosc, velocity), alpha=0.4) +

geom_smooth(aes(wilgotnosc, velocity)) +

labs(x="Wilgotność powietrza [%]", y="Średnia prędkość [km/h]")

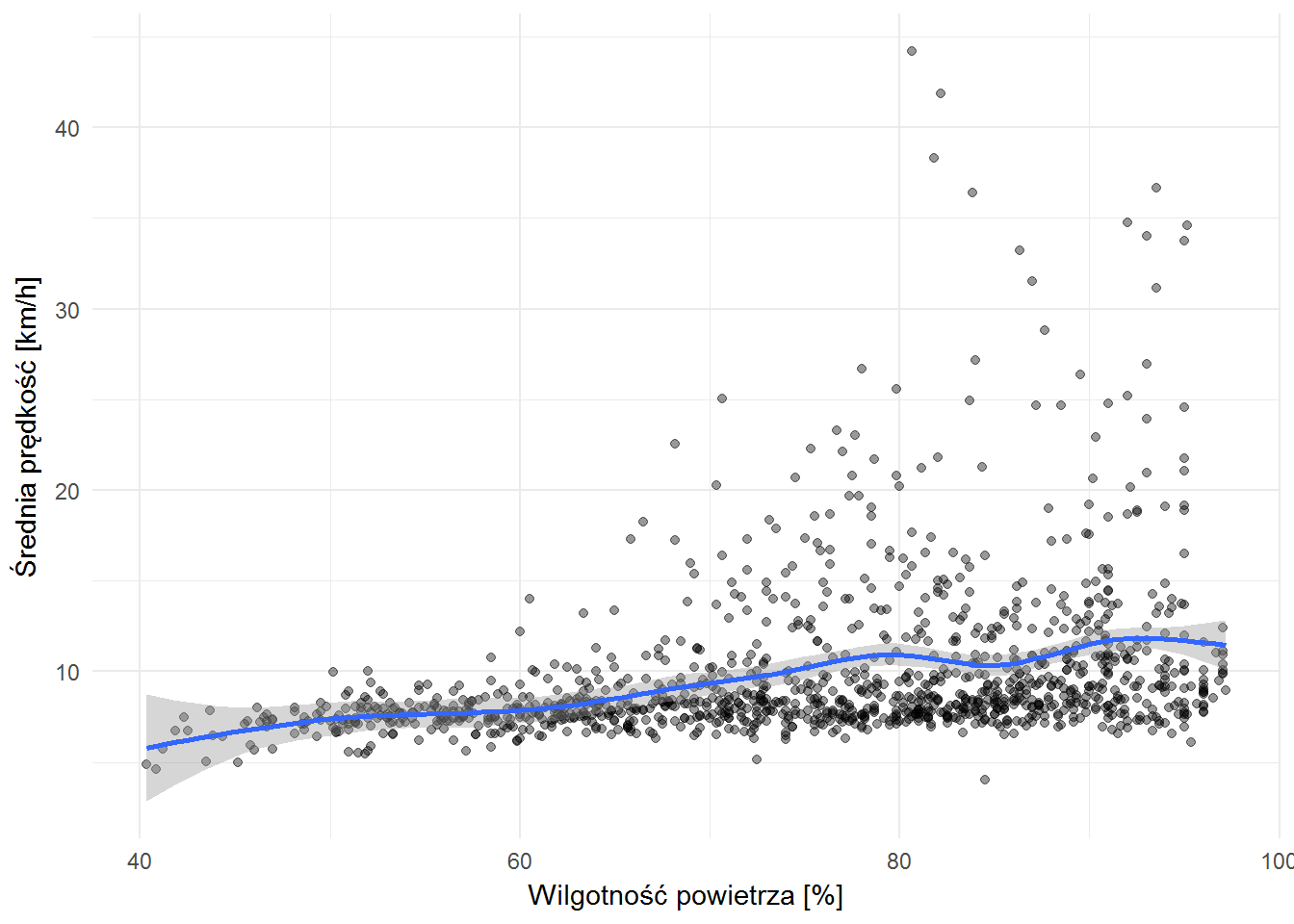
Im bardziej mokro tym większa prędkość. Wiadomo, trzeba uciekać przed deszczem.

Na koniec jeszcze zależność prędkości od pory dania (godziny):

ggplot(weather_velocity_by_hour) +
   geom_boxplot(aes(hour, velocity, group=hour),
                fill="lightgreen", color="darkgreen", alpha=0.8) +
   geom_smooth(aes(hour, velocity),
               color="darkred", size=2, se = FALSE) +
   labs(x="Godzina", y="Prędkość [km/h]")

ggplot(weather_velocity_by_hour) +

geom_boxplot(aes(hour, velocity, group=hour),

fill="lightgreen", color="darkgreen", alpha=0.8) +

geom_smooth(aes(hour, velocity),

color="darkred", size=2, se = FALSE) +

labs(x="Godzina", y="Prędkość [km/h]")

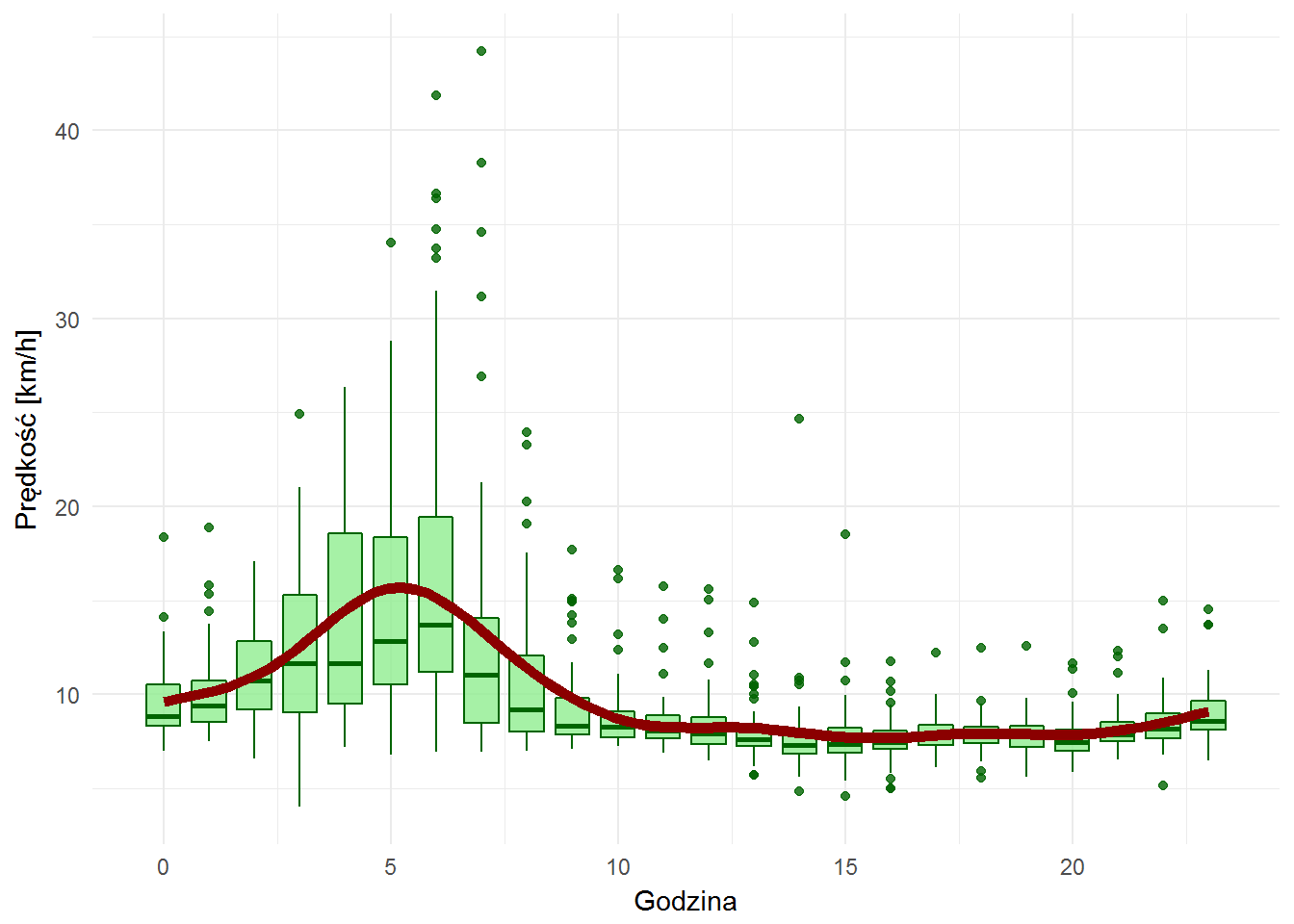
Można pokusić się o tezę, że nad ranem (4-6 rano) jest mały ruch na ulicach i ścieżkach rowerowych, więc da się jeździć szybciej. Widać też większą rozpiętość (większe prostokąciki) w tych porach, co może wskazywać na mniejszą ilość pomiarów i ich większe różnicowanie.

Wróćmy jeszcze do popularności tras – w tabeli wyżej (gdzieś w tych okolicach, po wykresie) widać było głównie trasy tam i z powtorem. Zobaczmy dwie najpopularniejsze:

Dewajtis-UKSW (stacja numer 9402) do Marymoncka-Dewajtis (stacja 9404) i z powrotem:

bikes_by_hour %>%
   filter(station_number %in% c(9402, 9404),
          station_number_p %in% c(9402, 9404)) %>%
   count(station_number, station_number_p, hour) %>%
   ungroup() %>%
   mutate(kierunek=ifelse(station_number == 9402,
                          "Dewajtis -> Marymoncka",
                          "Marymoncka -> Dewajtis")) %>%
   ggplot() +
   geom_line(aes(hour, n, color=kierunek), size=2) +
   labs(x="Godzina", y="Liczba przejazdów")

bikes_by_hour %>%

filter(station_number %in% c(9402, 9404),

station_number_p %in% c(9402, 9404)) %>%

count(station_number, station_number_p, hour) %>%

ungroup() %>%

mutate(kierunek=ifelse(station_number == 9402,

"Dewajtis -> Marymoncka",

"Marymoncka -> Dewajtis")) %>%

ggplot() +

geom_line(aes(hour, n, color=kierunek), size=2) +

labs(x="Godzina", y="Liczba przejazdów")

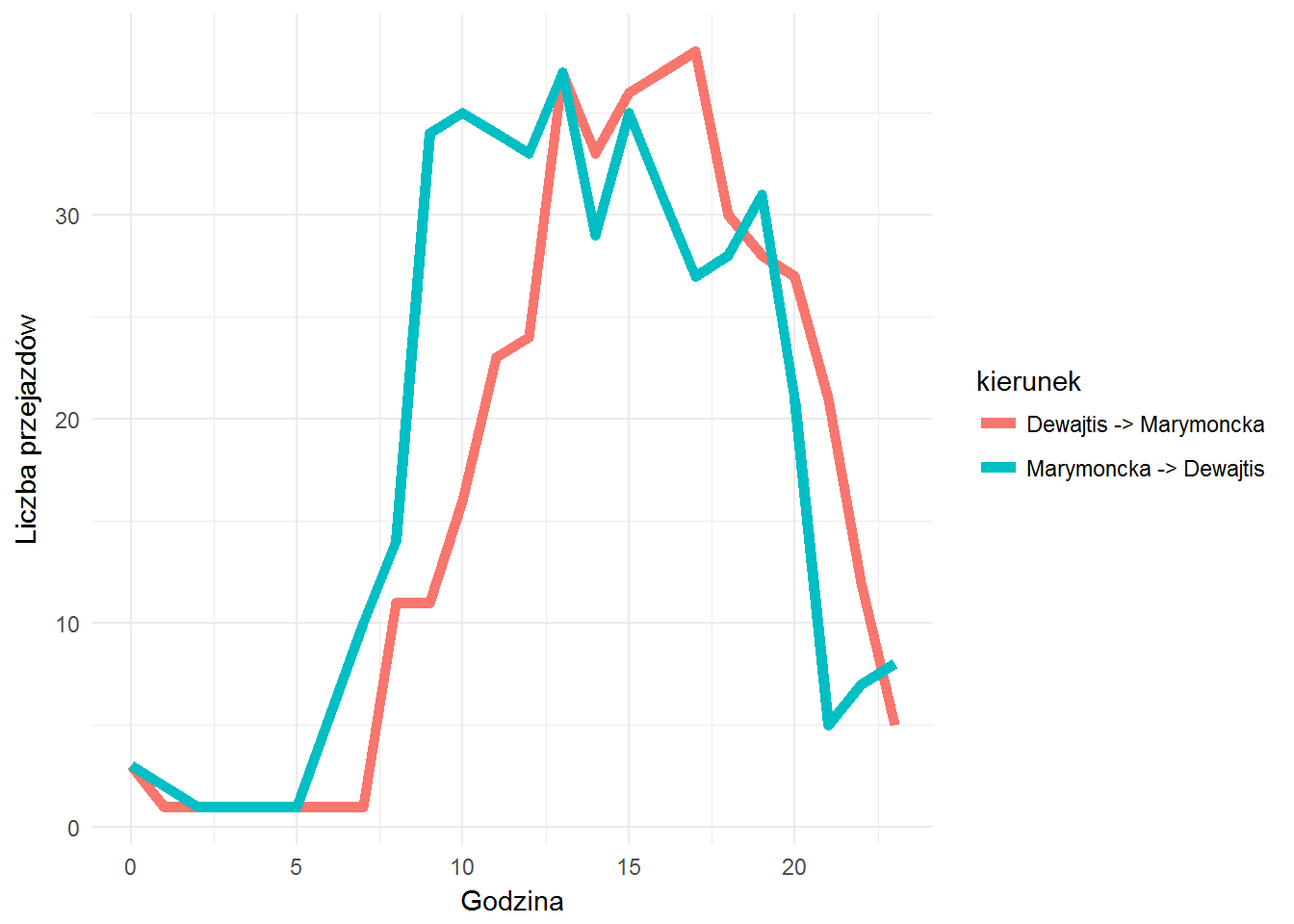
oraz al. Niepodległości-Batorego (9558) do Stefana Banacha-UW (9551) i z powrotem, ale tym razem w rozbicu na dni tygodnia:

bikes_by_hour %>%
   filter(station_number %in% c(9558, 9551),
          station_number_p %in% c(9558, 9551)) %>%
   mutate(wday = factor(wday(make_date(2017, month, day)),
                        levels = c(2, 3, 4, 5, 6, 7, 1),
                        labels = c("pn", "wt", "sr", "cz", "pt", "sb", "nd"))) %>%
   count(station_number, station_number_p, wday, hour) %>%
   ungroup() %>%
   mutate(kierunek=ifelse(station_number == 9558,
                          "al. Niepodległości -> Banacha",
                          "Banacha -> al. Niepodległości")) %>%
   ggplot() +
   geom_line(aes(hour, n, color=kierunek), size=1) +
   labs(x="Godzina", y="Liczba przejazdów") +
   facet_wrap(~wday)

bikes_by_hour %>%

filter(station_number %in% c(9558, 9551),

station_number_p %in% c(9558, 9551)) %>%

mutate(wday = factor(wday(make_date(2017, month, day)),

levels = c(2, 3, 4, 5, 6, 7, 1),

labels = c("pn", "wt", "sr", "cz", "pt", "sb", "nd"))) %>%

count(station_number, station_number_p, wday, hour) %>%

ungroup() %>%

mutate(kierunek=ifelse(station_number == 9558,

"al. Niepodległości -> Banacha",

"Banacha -> al. Niepodległości")) %>%

ggplot() +

geom_line(aes(hour, n, color=kierunek), size=1) +

labs(x="Godzina", y="Liczba przejazdów") +

facet_wrap(~wday)

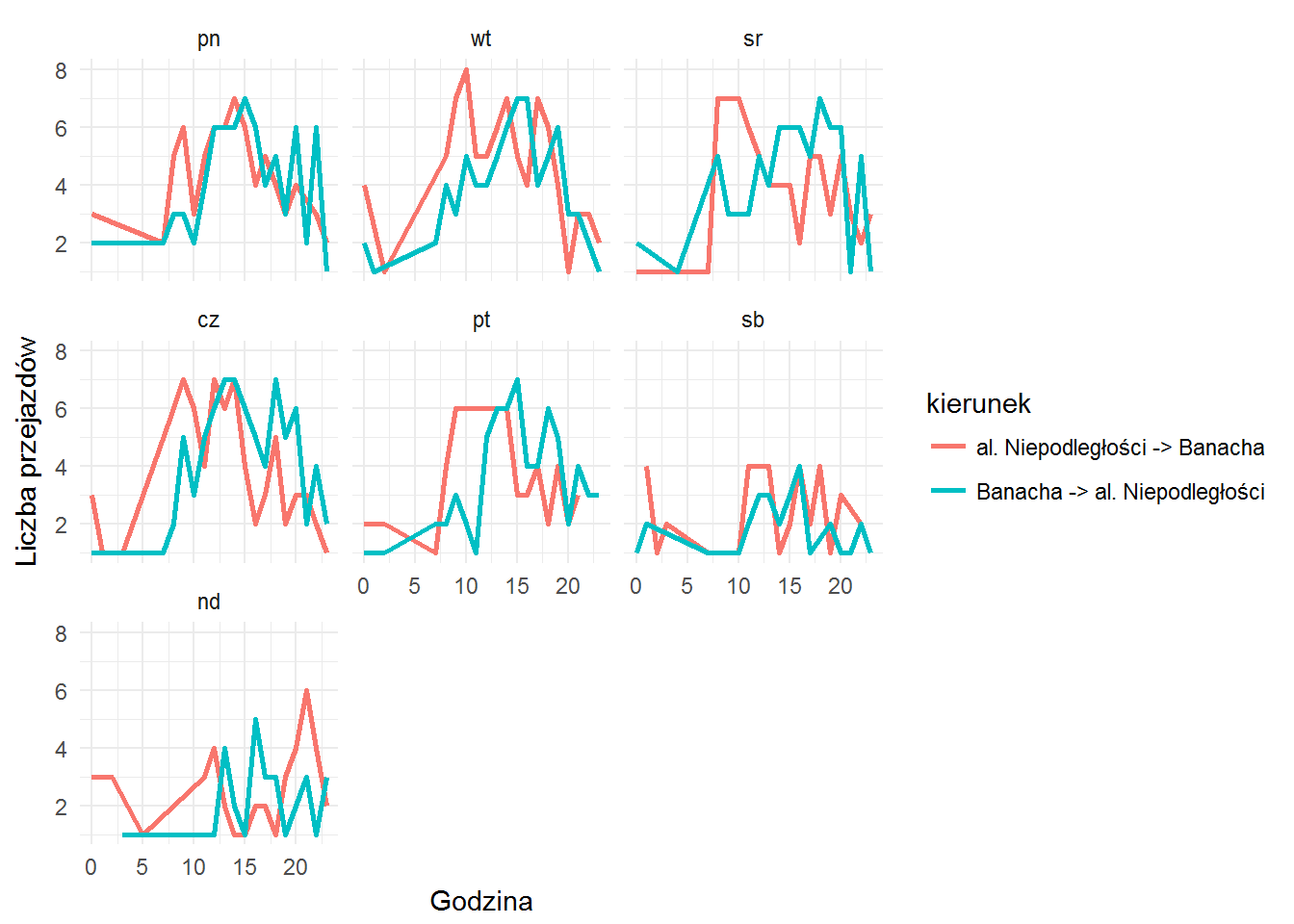
Tutaj piękie widać dojazd na Banacha przed południem i powrót po południu.

Warszawiacy wiedzą co jest w okolicy (dla obu par stacji), ciekawe czy przypuszczają co powoduje taki ruch? Podpowiem: UKSW i UW w nazwach stacji, a dodatkowo lokalizacja SGH oraz stacji metra.

Na dzisiaj to wszystko. Jeśli masz jakiekolwiek uwagi lub pytania – zostaw je w komentarzu.

6 komentarzy do “Rowery Veturilo – część druga”

Pingback: Veturilo a pogoda | Łukasz Prokulski
Łukasz 12-05-2017 o 16:02

Odpowiedz

Fajne opracowanie na temat poruszania się rowerem po Warszawie jest tu: http://rowerozofia.blox.pl/2016/03/Jak-jezdzimy-Veturilo.html
Dawid 13-05-2017 o 8:23

Odpowiedz

będzie ciekawie w wakacje jak na karcie multisport dodadzą startową 1h godzinę gratis.
1. Łukasz
  
  The Real Person!
  
  Author Łukasz acts as a real person and verified as not a bot.
  
  Passed all tests against spam bots. Anti-Spam by CleanTalk.
  
  The Real Person!
  
  Author Łukasz acts as a real person and verified as not a bot.
  
  Passed all tests against spam bots. Anti-Spam by CleanTalk.
  
  13-05-2017 o 9:58
  
  Odpowiedz
  
  Multisport już obowiązuje. To jest zdaje się godzina gratis zamiast 20 minut.
2. Maciek 13-05-2017 o 9:26
  
  Odpowiedz
  
  Super opracowanie!
  
  I kolejne uwagi :-)
  
  1. Nie wiem czy dobrze zrozumiałem, ale chyba nie uwzględniasz przejazdów, które zaczynają się i kończą w tej samej stacji.
  W danych, które ja zbieram (mniej więcej od początku kwietnia) to 3 najpopularniejsze trasy zaczynają się i kończą w tej samej stacji:
  – al. Niepodległości – Batorego
  – Rondo Waszyngtona – Stadion Narodowy
  – Stefana Banacha – UW
  
  Dane zbieram co minutę, jeżeli między jedną obecnością roweru w stacji a drugą jest chociaż minuta przerwy, to uznaję, że rower ją opuścił
  
  2. Z rozważań o prędkości wynika, że nie wszystkie transfery rowerów między stacjami, to przejazdy ludzi na rowerach. Tak jest w istocie: zgodnie z umową między miastem a NextBike, firma jest zobowiązana dokonywać między 22-8 rano transferów rowerów, tak by w każdej stacji było rano zajęte między 20%-80% stojaków.
3. 1. Łukasz
    
    The Real Person!
    
    Author Łukasz acts as a real person and verified as not a bot.
    
    Passed all tests against spam bots. Anti-Spam by CleanTalk.
    
    The Real Person!
    
    Author Łukasz acts as a real person and verified as not a bot.
    
    Passed all tests against spam bots. Anti-Spam by CleanTalk.
    
    13-05-2017 o 10:03
    
    Odpowiedz
    
    Tak, start i powrót na tej samej stacji wykluczam. Co do danych minutowych – powrót po minucie na tą samą stację to może być zwrot wadliwego roweru, to bym wykluczał (sam kilka razy tak robiłem, jak się zorientowałem że rower nie ma na przykład pedału)

Rowery Veturilo – część druga

Gdzie są stacje Veturilo?

Czy rowerem dojeżdza się do i z pracy?

Najpopularniejsze trasy rowerowe

Dygresja – pokazuję i objaśniam

Koniec przykładu

Średni czas trwania przejazdu pomiędzy stacjami

Jak szybko jeżdżą?

6 komentarzy do “Rowery Veturilo – część druga”

Dodaj komentarz Anuluj pisanie odpowiedzi