Jednym z głównych zagadnień w analizie danych jest klasyfikacja elementów do wybranych grup, na podstawie właściwości opisujących elementy. W pakiecie R i jego bibliotekach znajdziemy gotowe rozwiązania, pytanie tylko którego użyć?
Zanim jednak coś poklasyfikujemy – zastanówmy się do czego to może być potrzebne?
Zastosowań jest bardzo dużo:
- zaszeregowanie gatunków roślin na podstawie parametrów typu długość liścia (bardzo popularny zestaw danych iris opisujący pąki irysów trzech odmian)
- nieco ryzykowne – określanie czy grzyb jest jadalny czy też nie
- filtrowanie spamu na podstawie nadawcy i zawartości maila
- określanie autora tekstu na podstawie samego tekstu (w uproszczeniu na podstawie częstości występowania słów – pojedynczych jak i zbitek wyrazów)
- wykrywanie nadużyć w bankach lub firmach ubezpieczeniowych – tutaj ilość cech (parametrów określających np. transakcję kartą kredytową) jest ogromna
- podział klientów sklepu na określone grupy na podstawie zawartości koszyków
- i tak dalej, i tak dalej
My będziemy testować algorytmy klasyfikujące. Narysujemy sobie pięć “rozedrganych” kółek (precyzyjniej: okręgów) nachodzących na siebie (jak generator losowy pozwoli :-) i później dla każdego narysowanego punktu określimy do którego kółka należy. Coś, co widać gołym ludzkim okiem na obrazku nie zawsze jest takie łatwe do zobaczenia dla maszyny.
Post jest stricte edukacyjny, chyba niewiele ciekawych wniosków z danych tutaj wysnujemy. Chcę pokazać jakie są algorytmy (bez wchodzenia w ich szczegóły – klikaj w linki jeśli chcesz zgłębić wiedzę) i jak w najprostszej wersji użyć ich w R.
Jeśli Cię to trochę zniechęciło, to skroluj dalej, pooglądaj kolorowe okręgi. I to bez wychodzenia na pole (w sensie “w zboże”)!
Zaczynamy od przygotowania kółek. Danych.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
library(ggplot2) library(reshape2) library(gridExtra) # ustawienie generatora losowego set.seed(12345) # liczba kółek n_kol <- 5 # losowe promienie i środki kół radius <- sample(seq(1, 100, 10), n_kol) mid_x <- sample(seq(-50, 50, 5), n_kol) mid_y <- sample(seq(-50, 50, 5), n_kol) # przygotowanie kółek df <- data.frame(x=as.numeric(), y=as.numeric(), kolo=as.character()) for(i in 1:n_kol) { x <- mid_x[i] + radius[i] * sin(seq(0, 2*pi, pi/90)) + rnorm(181, 0, 5) y <- mid_y[i] + radius[i] * cos(seq(0, 2*pi, pi/90)) + rnorm(181, 0, 5) df <- rbind(df, data.frame(x=x, y=y, kolo=rep(i, 181))) } |
Powyżej standardowo – biblioteki, losowe położenie kółek, i zgodne z matematyką wyliczenie punktów na płaszczyźnie należących do koła o zadanym promieniu i środku. Z matematyki (ze szkoły średniej) oczywiście pamiętamy, że do koła (właściwie okręgu – koło jest pełne w środku) należą punkty spełniające równanie
![]()
z czego można dojść do
![Rendered by QuickLaTeX.com \[\begin{cases} x = x_0 + r \cos \alpha \\ y = y_0 + r \sin \alpha \end{cases}\]](https://quicklatex.com/cache3/84/ql_496911ed1fc8b5025c3c0eb7e2248984_l3.png)
gdzie ![]() .
.
Ale dość szpanowania matematyką na poziomie matury (mam nadzieję… że maturzyści tego jeszcze się uczą).
Wybierzmy sobie 70% punktów z każdego okręgu (dlatego w pętli – żeby wybierać po 70% z każdego, a nie po prostu 70% danych) jako dane treningowe i narysujmy nasze okręgi (dalej zwane potocznie kołami :) – te z kompletnych danych oraz te “treningowe”.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
df$kolo <- as.factor(df$kolo) # dane treningowe, 70% część całości df_train <- data.frame() for(i in 1:n_kol) { id <- sample(181, 0.7*181)+181*(i-1) df_train <- rbind(df_train, df[id, 1:3]) } # koła "pełne" kola_all <- ggplot(df) + geom_point(aes(x,y,color=kolo, shape=kolo), size=2, show.legend=FALSE) + coord_fixed() + theme_void() # koła "treningowe" kola_train <- ggplot(df_train) + geom_point(aes(x,y,color=kolo, shape=kolo), size=2, show.legend=FALSE) + coord_fixed() + theme_void() grid.arrange(kola_all, kola_train, ncol=2) |

Jak widać jedno (to z prawej) koło (okrąg! jak rany…) takie bardziej rzadkie niż drugie. Tak ma być.
k-średnich
|
1 2 3 |
# k-means kmns <- kmeans(df[,1:2], n_kol) df$kolor_kmns <- as.factor(kmns$cluster) |
W dużym uproszczeniu algorytm szuka n_kol punktów-środków, od których pozostałe punkty są jak najmniej oddalone (taki “środek skupienia”). Później dla wszystkich punktów i środków oblicza wzajemne odległości punkt-środek. Punkt zostaje przypisany do grupy (jednej z n_kol), do której środka ma najbliżej.
Zobaczmy co wyszło:
|
1 2 3 4 5 |
ggplot(df) + geom_point(aes(x,y,color=kolor_kmns, shape=kolo), size=2) + coord_fixed() + labs(shape="Koło oryginalne", color="k-means") + theme_void() |
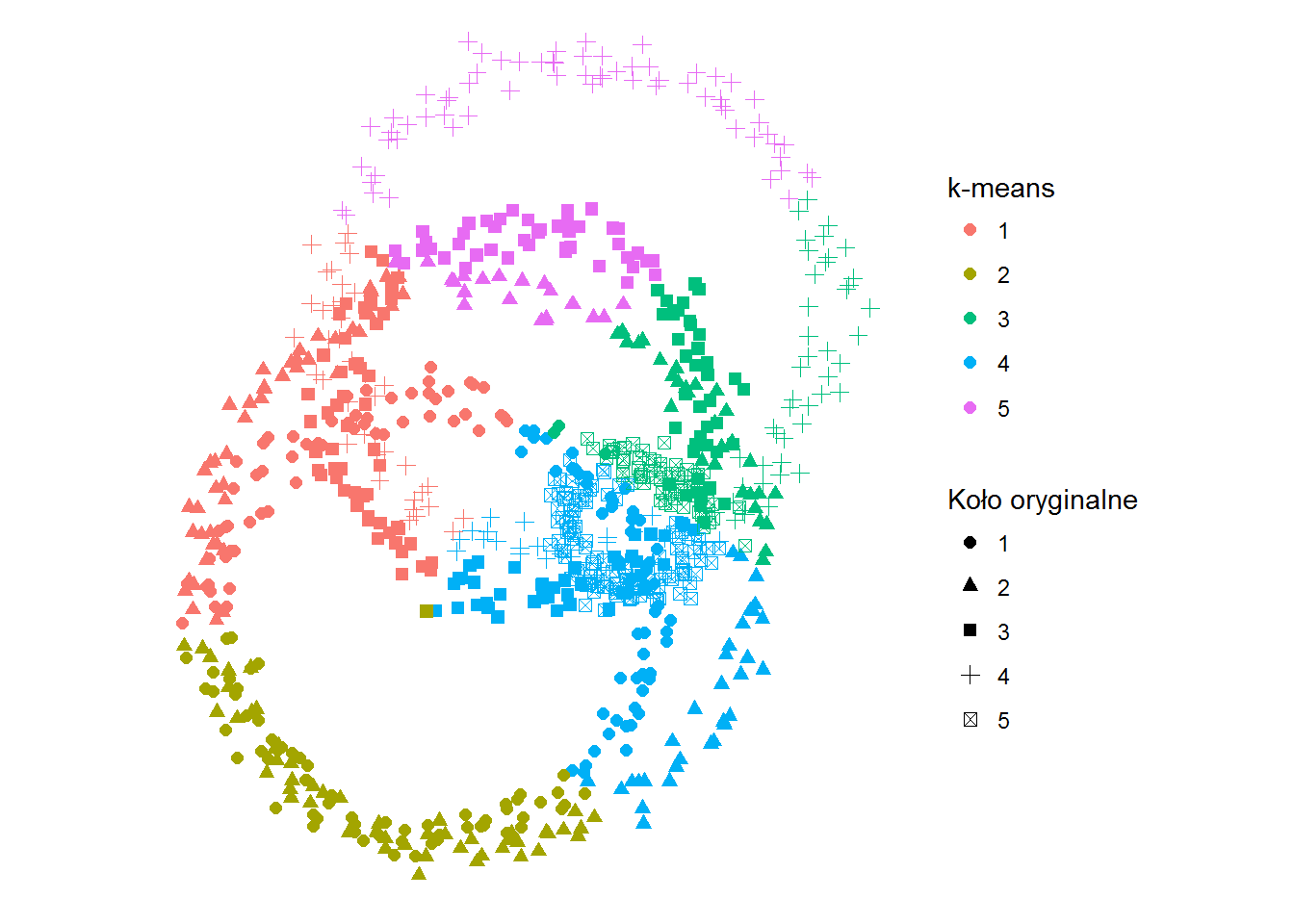
Kolorem oznaczone jest dopasowanie według zadanego algorytmu, symbolem – oryginalny okrąg. Jak widać k-średnich przypisało punkty po odległościach od jakiegoś środka, a nie po okręgach.
Możemy teraz sprawdzić ile punktów “przeszło” w modelu z jednego koła do drugiego. Im mniej tym lepiej oczywiście.
W tabelce poniżej w wierszach mamy koła wymodelowane, w rzędach – koła oryginalne. Liczba na przecięciu mówi o tym ile punktów okręgu oryginalnego zawiera okrąg powstały w wyniku klasyfikacji.
Takie operacje będziemy powtarzać też dla kolejnych modeli.
|
1 2 3 |
cm <- as.matrix(table(Oryginal=df$kolo, Predicted=df$kolor)) print(cm) accuracy_kmns <- sum(diag(cm))/sum(cm) |
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 1 | 59 | 64 | 3 | 55 | 0 |
| 2 | 47 | 52 | 30 | 31 | 21 |
| 3 | 55 | 1 | 40 | 42 | 43 |
| 4 | 40 | 0 | 45 | 29 | 67 |
| 5 | 0 | 0 | 61 | 120 | 0 |
Policzmy na ile dobrze dopasowaliśmy naszym modelem dane. Bez takiego wskaźnika nie uda się stwierdzić czy model jest dobry oraz który jest lepszy. Metod jest wiele, w przypadku kategoryzacji najprostszy to sprawdzenie ile punktów zostało dobrze zaklasyfikowanych w stosunku do wszystkich punktów. Matematycznie jest to suma wartości na przekątnej w powyższej tabeli (sum(diag(cm))) podzielona przez sumę wszystkich elementów tabeli (sum(cm)).
Dokładność dopasowania jaką osiągamy w przypadku k-średnich to 19.9%. Nie powala, ale to widać już na obrazku.
Gdyby koła były mniejsze i ciaśniej (o zbliżonych środkach) byłoby jeszcze gorzej. To fajny i stosunkowo szybki algorytm dla danych, których grupy są mocno rozrzuconych od siebie i jednocześnie elementy grup są dobrze skupione w ramach samej grupy. Coś jak winogrona w kiściach – każda kiść jest “zbita” z pojedynczych winogron, a same kiście są na tyle daleko od siebie, że można je łatwo odróżnić od siebie.
Są metody (np. PCA – po polsku analiza głównych składowych), które pozwalają znaleźć przekształcenie punktów do innej płaszczyzny, na której już algorytm k-średnich zadziała zdecydowanie lepiej. Kiedyś się tym zajmiemy.
Naiwny Bayes
|
1 2 3 4 |
# naive Bayes library(e1071) bayes <- naiveBayes(kolo ~ x + y, data=df[,1:3]) df$kolor_bayes <- predict(bayes, df[,1:3]) |
Jak widać stworzenie modelu jest zupełnie banalne, i identyczne z k-średnimi. Tak samo będzie dla kolejnych.
Na czym polega naiwny Bayes? Na prawdopodobieństwie – na podstawie warunkowego prawdopodobieństwa dla znanych uwarunkowań określamy prawdopodobieństwo dla czegoś nowego. Opisuje to twierdzenie Bayesa:
![]()
Popularne przykłady (np. opisane w Wikipedii) mówią o grypie (jeśli ktoś ma gorączkę i ból głowy to czy ma grypę? Skoro ileś procent osób z gorączką ma grypę i analogicznie dla bólu głowy) albo rozpoznaniu owoców (po kształcie, kolorze i smaku).
Co jest ważne przy twierdzeniu Bayesa to fakt, że dana “kombinacja” czynników musi zdarzyć się co najmniej raz (aby prawdopodobieństwo nie było zerowe). Sam algorytm jest szybki – dla nauczonych danych właściwe wystarczy operować na stablicowanych wartościach. A jak się sprawdza?
|
1 2 3 4 5 |
ggplot(df) + geom_point(aes(x,y,color=kolor_bayes, shape=kolo), size=2) + coord_fixed() + labs(shape="Koło oryginalne", color="naive Bayes") + theme_void() |
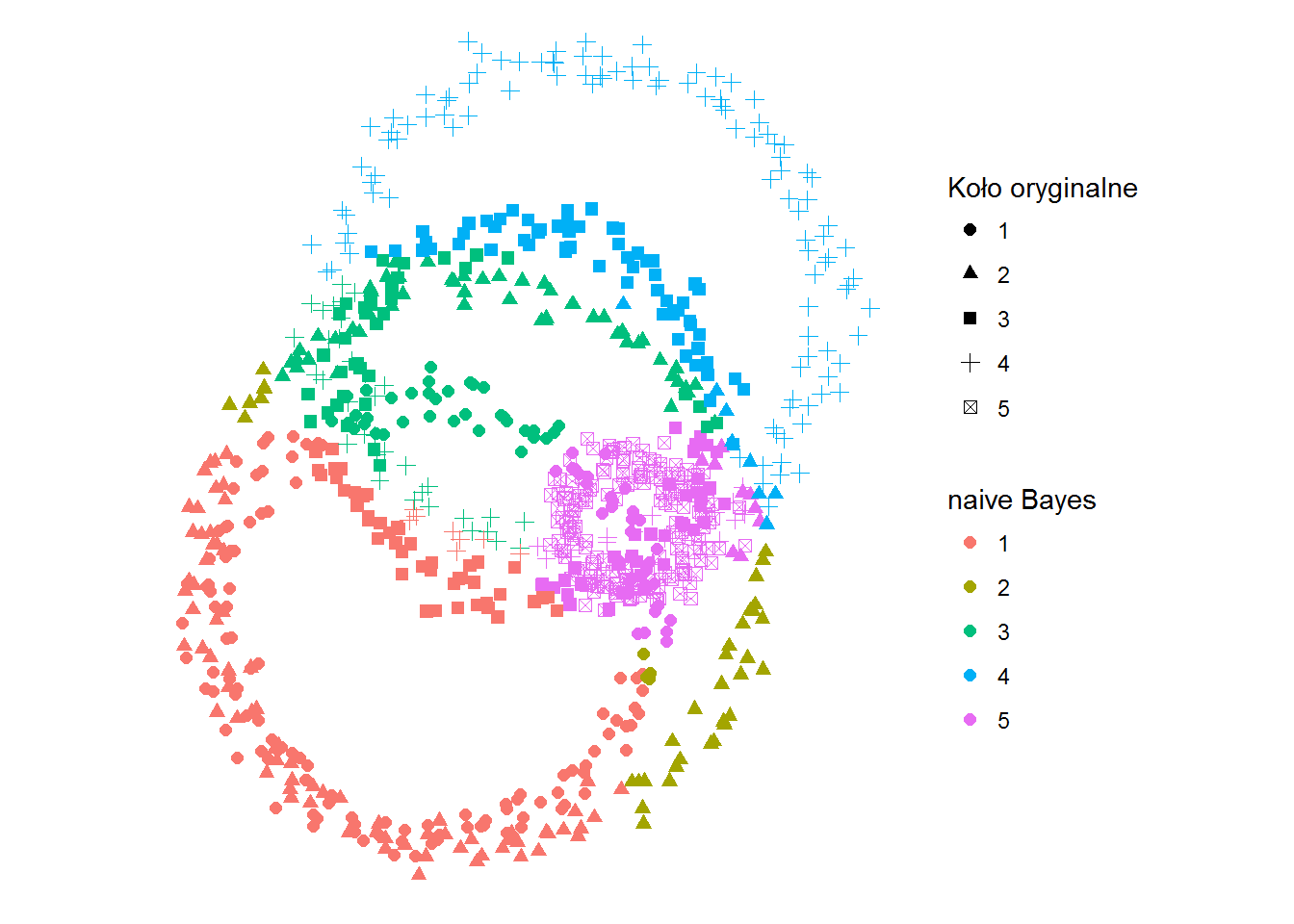
I jeszcze tabelka:
|
1 2 3 |
cm <- as.matrix(table(Oryginal=df$kolo, Predicted=df$kolor_bayes)) print(cm) accuracy_nb <- sum(diag(cm))/sum(cm) |
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 1 | 110 | 4 | 36 | 0 | 31 |
| 2 | 76 | 36 | 52 | 8 | 9 |
| 3 | 45 | 0 | 37 | 60 | 39 |
| 4 | 8 | 0 | 36 | 111 | 26 |
| 5 | 0 | 0 | 0 | 0 | 181 |
Dokładność dopasowania jaką osiągamy to 52.5%
Jest zdecydowanie lepiej. Ale to tylko nieco ponad połowa trafnych przypadków – trochę jak w rzucie monetą.
SVM (Supported Vector Machine)
Polska nazwa to maszyna wektorów wspierających lub nośnych.
|
1 2 3 4 |
# SVM library(e1071) model_svm <- svm(kolo ~ x + y, data=df[,1:3]) df$kolor_svm <- predict(model_svm, df[,1:3]) |
Algorytm polega na znalezieniu takiej płaszczyzny rozdzielającej, dla której uda się znaleźć maksymalny margines (odległość punktów od płaszczyzny), dla których przeprowadzamy klasyfikację. Wówczas punkty z jednej strony marginesu należą do jednej klasy, a z drugiej – do drugiej.
|
1 2 3 4 5 |
ggplot(df) + geom_point(aes(x,y,color=kolor_svm, shape=kolo), size=2) + coord_fixed() + labs(shape="Koło oryginalne", color="SVM") + theme_void() |
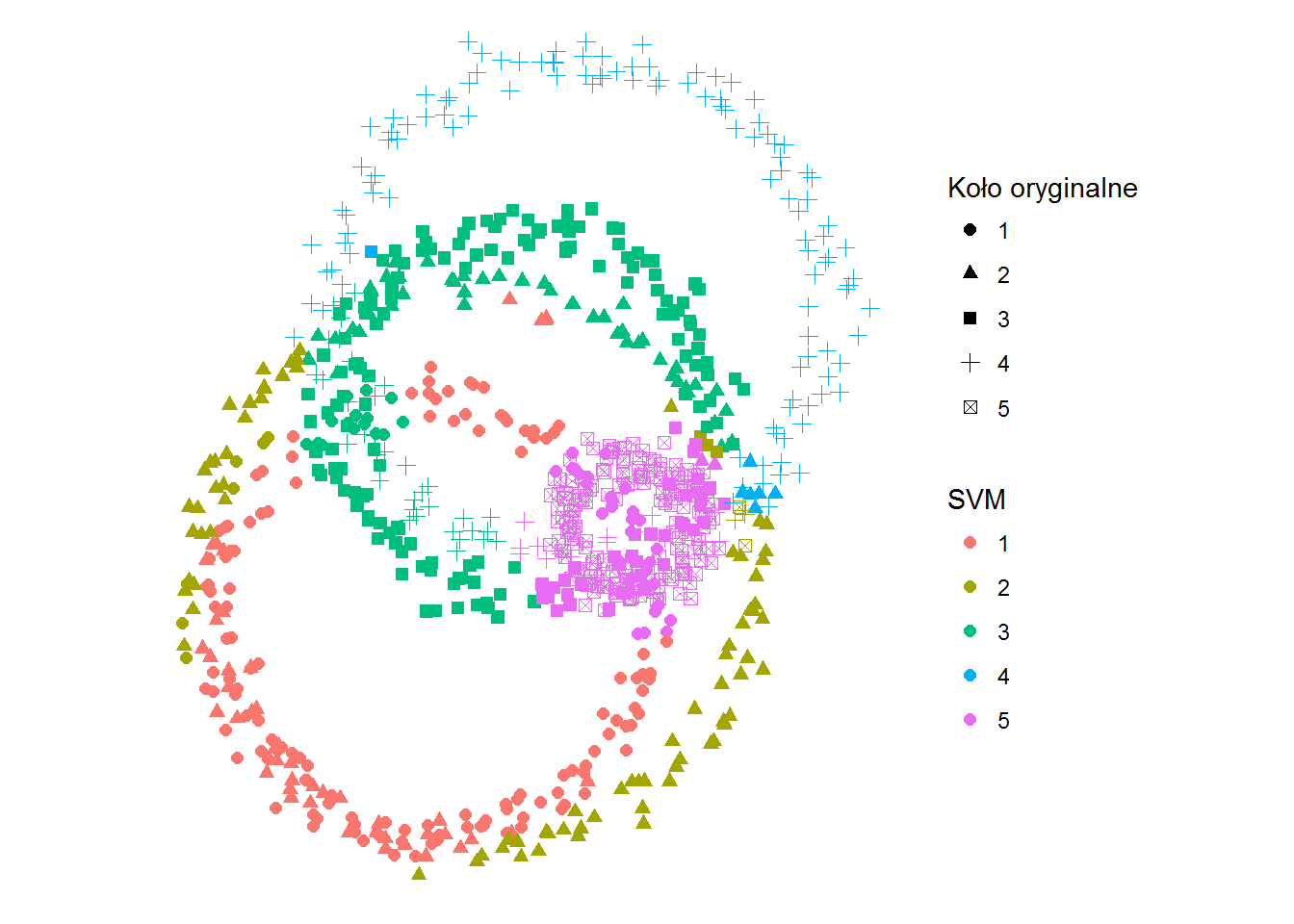
|
1 2 3 |
cm <- as.matrix(table(Oryginal=df$kolo, Predicted=df$kolor_svm)) print(cm) accuracy_svm <- sum(diag(cm))/sum(cm) |
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 1 | 128 | 7 | 16 | 0 | 30 |
| 2 | 47 | 79 | 47 | 6 | 2 |
| 3 | 0 | 3 | 138 | 1 | 39 |
| 4 | 0 | 3 | 37 | 117 | 24 |
| 5 | 0 | 2 | 0 | 0 | 179 |
Dokładność dopasowania jakę osiągamy to 70.8%. Niesamowite prawda? I to dość szybkie – algorytm ten stosowany jest w aparatach fotograficznych do rozpoznawania twarzy, co jest przydatne przy autofokusie na twarz.
Drzewa decyzyjne
|
1 2 3 |
# tree library(tree) model_tree <- tree(kolo ~ x + y, data=df[,1:3]) |
Drzewko możemy sobie narysować. Dlatego drzewa są fajne – łatwo je zobrazować. I łatwo wytłumaczyć.
|
1 2 |
plot(model_tree) text(model_tree) |
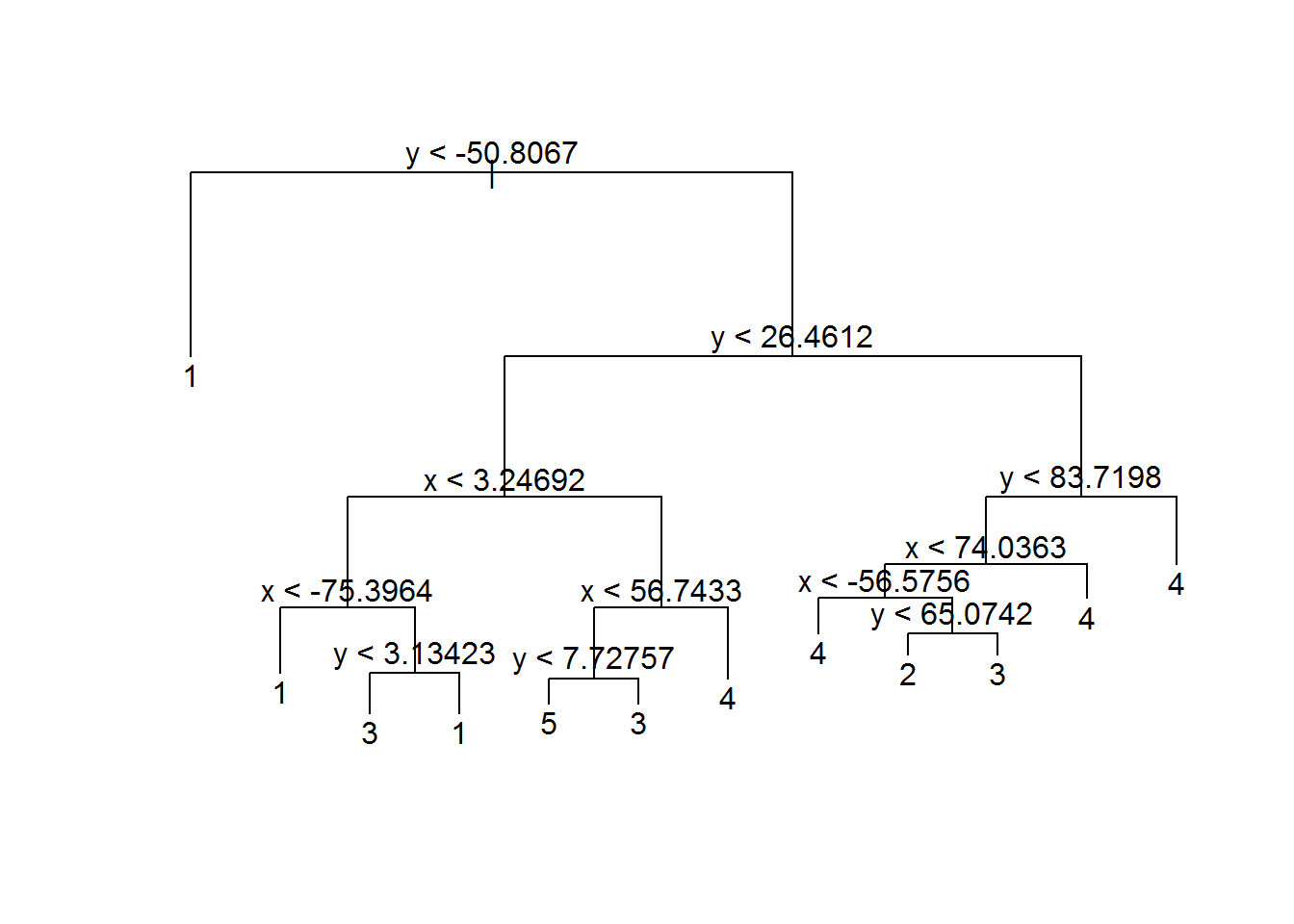
Drzewa decyzyjne to najprościej mówiąc przejście przez kolejne kroki, w których możemy wybrać – idziemy w lewo albo w prawo (warunek, który badamy jest spełniony albo nie).
Biblioteka tree jest jeszcze z innego powodu fajna (poza rysowaniem drzewek). Nie dostajemy zero-jedynkowych klasyfikacji, a prawdopodobieństwo dopasowania do określonej grupy. Zobaczmy:
|
1 2 |
tree_predict <- predict(model_tree, df[,1:3]) tree_predict[sample(1:nrow(tree_predict), 10), ] |
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 830 | 10.2 | 0.4 | 13.3 | 6.6 | 69.5 |
| 819 | 10.2 | 0.4 | 13.3 | 6.6 | 69.5 |
| 738 | 10.2 | 0.4 | 13.3 | 6.6 | 69.5 |
| 611 | 0.0 | 41.5 | 9.4 | 43.4 | 5.7 |
| 438 | 10.2 | 0.4 | 13.3 | 6.6 | 69.5 |
| 440 | 10.2 | 0.4 | 13.3 | 6.6 | 69.5 |
| 141 | 50.0 | 50.0 | 0.0 | 0.0 | 0.0 |
| 84 | 53.6 | 46.4 | 0.0 | 0.0 | 0.0 |
| 245 | 53.6 | 46.4 | 0.0 | 0.0 | 0.0 |
| 434 | 10.2 | 0.4 | 13.3 | 6.6 | 69.5 |
Liczby w tabeli to procent prawdopodobieństwa przynależności określonego punktu (w wierszach) do grupy (w kolumnach).
My jednak potrzebujemy dokładnie powiedzieć do którego okręgu należy punkt. Przygotujemy więc funkcję, która wybierze grupę z maksymalnym prawdopodobieństwem.
|
1 2 3 4 5 6 |
max_prob <- function(x) { return(names(x)[which(x==max(x), arr.ind = TRUE)[1]]) } df$kolor_tree <- apply(tree_predict, 1, max_prob) |
Co z tego wszystkiego wychodzi?
|
1 2 3 4 5 |
ggplot(df) + geom_point(aes(x,y,color=kolor_tree, shape=kolo), size=2) + coord_fixed() + labs(shape="Koło oryginalne", color="tree") + theme_void() |
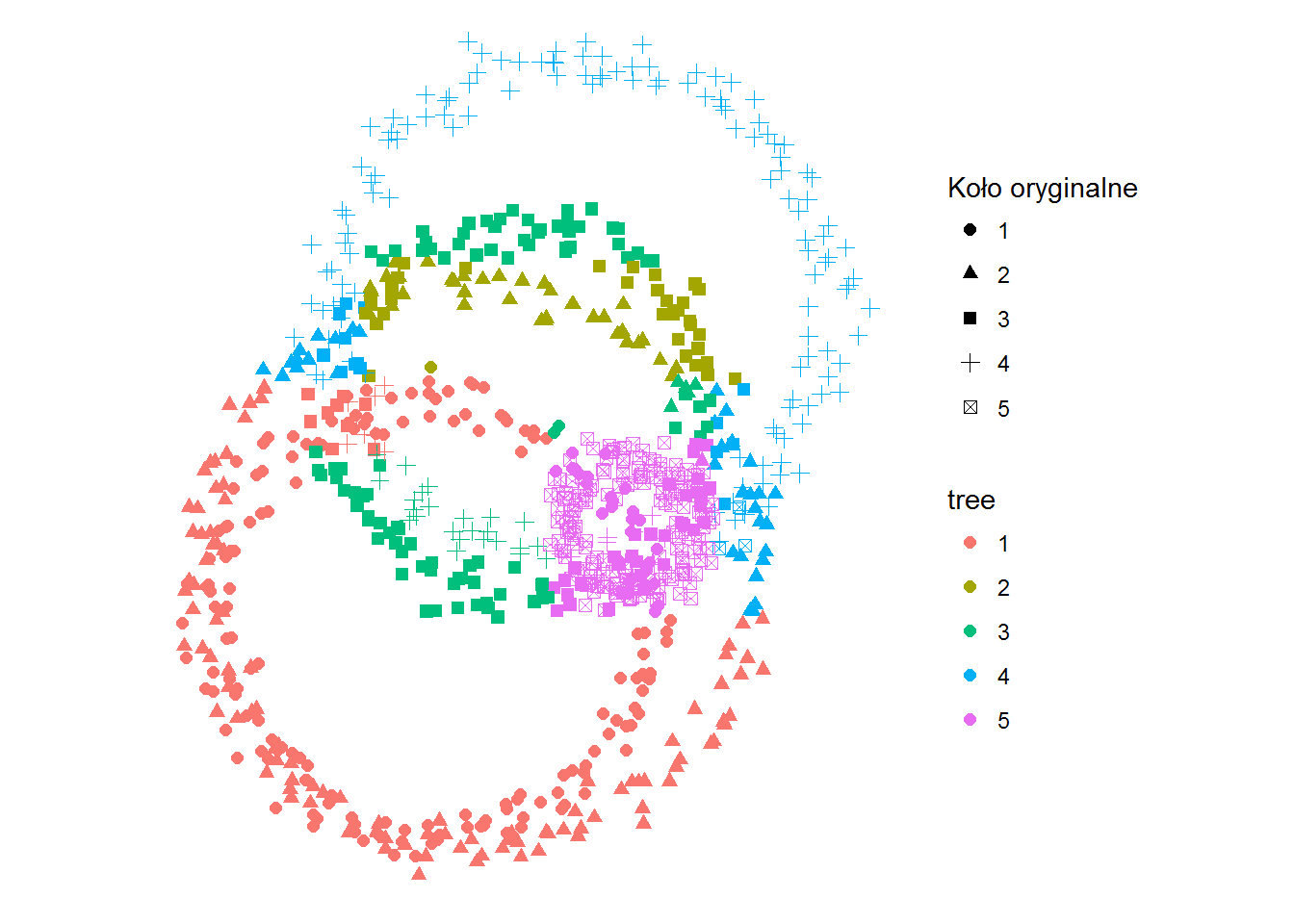
Jak dokładnie przyjrzycie się schematowi drzewa to za przypisane do konkretnego okręgu odpowiada położenie punktu – niżej niż Y = -50.8 to okrąg 1. Dla innych wartości zaczyna się to rozgałęziać. Ale koniec końców można wyznaczyć proste (zarówno na osi X jak i Y), które rozdzielą nasz obraz na kilka prostokątnych obszarów. I to tak naprawdę te obszary określają docelową grupę.
|
1 2 3 |
cm <- as.matrix(table(Oryginal=df$kolo, Predicted=df$kolor_tree)) print(cm) accuracy_tree <- sum(diag(cm))/sum(cm) |
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 1 | 152 | 1 | 2 | 0 | 26 |
| 2 | 105 | 36 | 5 | 34 | 1 |
| 3 | 9 | 33 | 91 | 14 | 34 |
| 4 | 8 | 0 | 24 | 132 | 17 |
| 5 | 0 | 0 | 0 | 3 | 178 |
Dokładność dopasowania jaką osiągamy tym razem to 65.1%
Drzewa łatwo “przetrenować” – wyniki są zbyt dopasowane do próbek uczących. Można drzewa “przycinać” albo zbudować las drzew, wybierając losową ilość próbek i losową ilość parametrów określających grupę. A w dodatku powiedzieć, że decydujemy w skończonej liczbie kroków, a nie do samego końca. Coś takiego robi kolejna metoda.
Random Forest czyli Losowy las drzew decyzyjnych
|
1 2 3 4 |
# Random Forest library(randomForest) model_forest <- randomForest(kolo ~ x + y, data=df_train) df$kolor_rforest <- predict(model_forest, df[,1:3]) |
|
1 2 3 4 5 |
ggplot(df) + geom_point(aes(x,y,color=kolor_rforest, shape=kolo), size=2) + coord_fixed() + labs(shape="Koło oryginalne", color="random forest") + theme_void() |
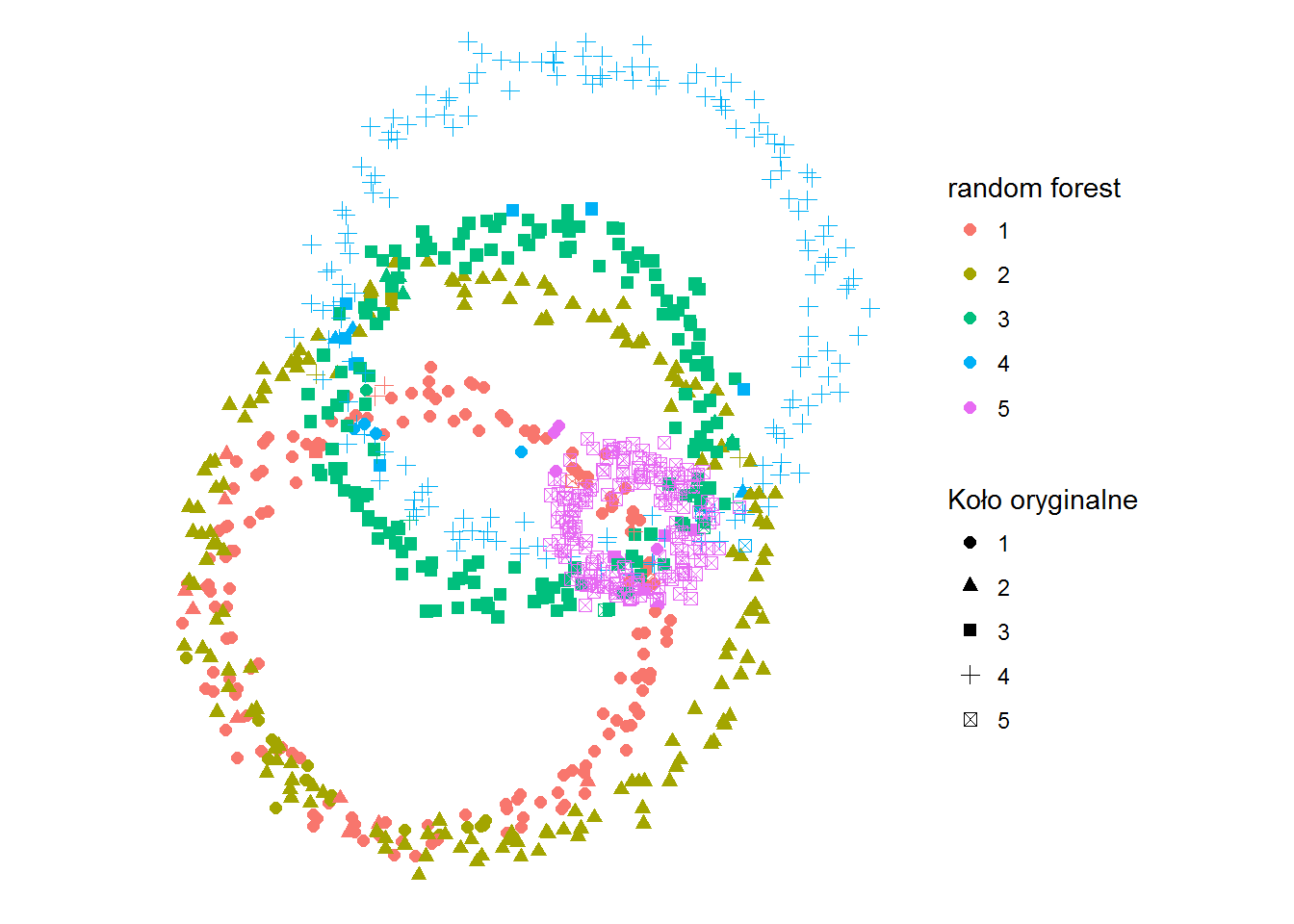
Wow! Wreszcie mamy coś, co przypomina okręgi, już po podziale! I to nawet takie dość dobrze pasujące do danych źródłowych:
|
1 2 3 |
cm <- as.matrix(table(Oryginal=df$kolo, Predicted=df$kolor_rforest)) print(cm) accuracy_rf <- sum(diag(cm))/sum(cm) |
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 1 | 154 | 16 | 1 | 4 | 6 |
| 2 | 9 | 164 | 5 | 3 | 0 |
| 3 | 1 | 2 | 166 | 8 | 4 |
| 4 | 3 | 2 | 3 | 168 | 5 |
| 5 | 3 | 0 | 3 | 2 | 173 |
Dokładność dopasowania jaką osiągamy to 91.2%. Dlatego lubię metodę random forest :) Z jednej strony daje naprawdę dobre wyniki, a z drugiej – jest stosunkowo prosta to wyjaśnienia (ot, dużo drzew decyzyjnych, losowo wybieranych). Przy dodatkowych parametrach można wynik jeszcze trochę poprawić.
XGBoost czyli objawienie konkursów Kaggle.com
|
1 2 3 4 5 6 7 8 9 10 11 |
# XGBoost library(xgboost) model_xgb <- xgboost(data = as.matrix(df_train[,1:2]), label = as.numeric(as.character(df_train[,3]))-1, nround = 50, objective = "multi:softmax", num_class = n_kol, eval_metric = "merror", verbose = 0) df$kolor_xgb <- predict(model_xgb, as.matrix(df[,1:2])) df$kolor_xgb <- as.factor(df$kolor_xgb + 1) |
XGBoost to dość młoda biblioteka, która w dużym uproszczeniu działa na budowie drzew decyzyjnych w różnych ujęciach cech, a następnie składa te drzewa razem. Taki bardziej rozbudowany random forest.
|
1 2 3 4 5 |
ggplot(df) + geom_point(aes(x,y,color=kolor_xgb, shape=kolo), size=2) + coord_fixed() + labs(shape="Koło oryginalne", color="xgboost") + theme_void() |
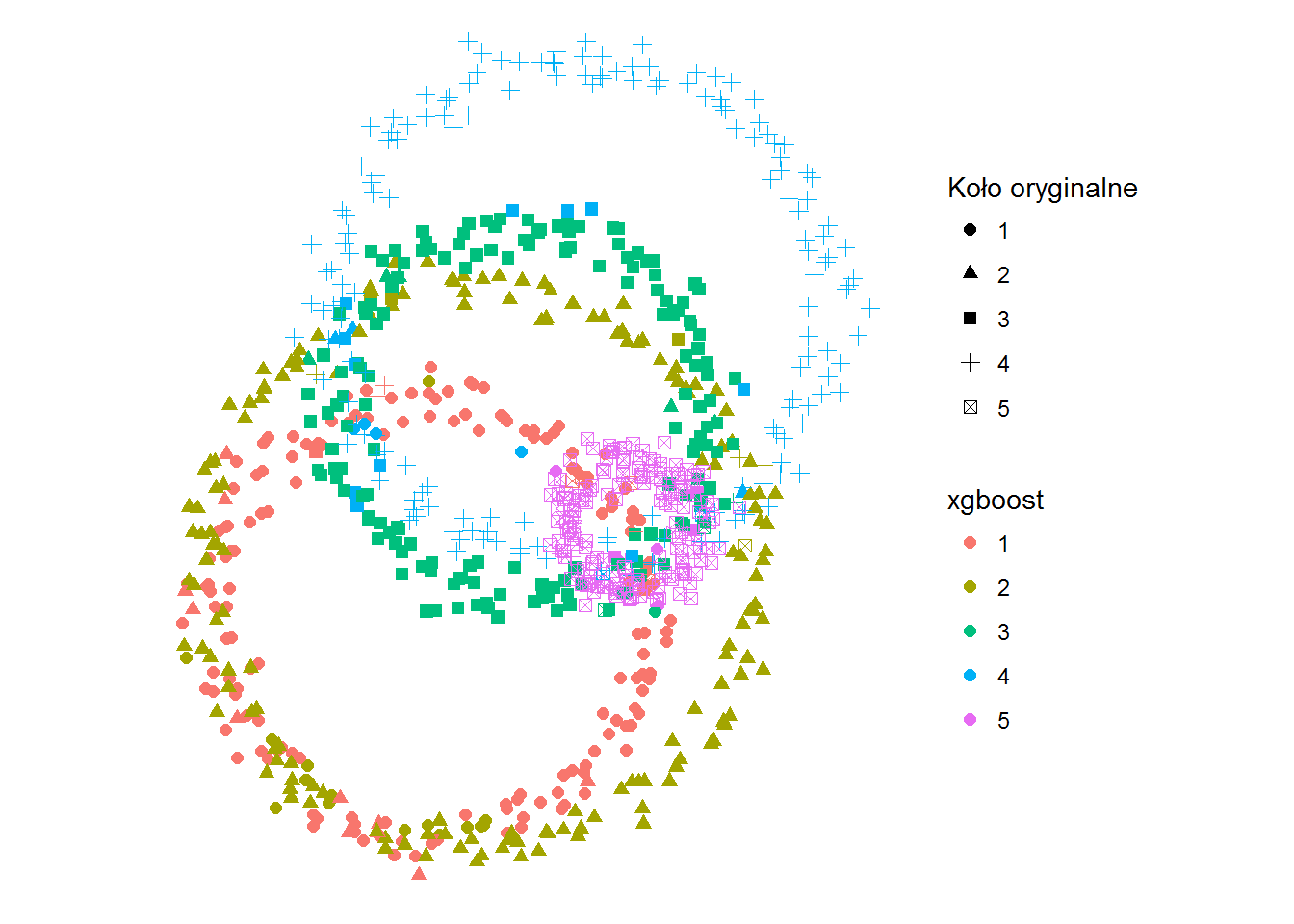
Na pierwszy rzut oka wygląda świetnie, tak dobrze jak random forest. Jak to wygląda w szczegółach?
|
1 2 3 |
cm <- as.matrix(table(Oryginal=df$kolo, Predicted=df$kolor_xgb)) print(cm) accuracy_xgb <- sum(diag(cm))/sum(cm) |
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 1 | 155 | 17 | 1 | 4 | 4 |
| 2 | 11 | 162 | 5 | 3 | 0 |
| 3 | 2 | 3 | 162 | 11 | 3 |
| 4 | 3 | 3 | 1 | 168 | 6 |
| 5 | 4 | 1 | 2 | 2 | 172 |
Dokładność dopasowania jaką osiągamy to 90.5% czyli blisko poprzedniej metody. I tak to zazwyczaj jest, chociaż pewnie przy bardziej skomplikowanych danych wypada różnie.
Dla naszego zadania “do którego okręgu należy punkt?” zrobiłem symulację różnej ilości okręgów (za każdym razem losowych) z różną “gęstością” punktów w okręgu obie metody dały podobne (najwyższe) wyniki, właściwie bez wskazania zwycięzcy. Jednak jestem gotów uwierzyć w to co widać po wynikach na Kaggle – dla bardziej skomplikowanych (większa ilość danych) zbiorów XGBoost daje lepsze efekty. Niewiele, ale jednak.
Podsumowanie metod
Dla przypomnienia wszystkie wyniki dokładności dopasowania:
- kmeans – 19.9%
- naive Bayes – 52.5%
- SVM – 70.8%
- Tree – 65.1%
- Random Forest – 91.2%
- XGBoost – 90.5%
K-średnich zdecydowanie najsłabiej, lasy losowe (XGBoost to w zasadzie ich odmiana) najlepiej.
Na koniec ciekawostka – wpis ten zacząłem pisać jeszcze w lutym, ale ciekawsze dane (między innymi Oscary) były bardziej na czasie niż teoria. Ostatnio trafiłem na blog Mateusza Grzyba, na którym możecie przeczytać znakomite uzupełnienie tego co już wiecie.
Fajny artykuł. Wczytuję się w resztę treści bloga i… jest świetnie! :)
Dodane do RSS, a więc będę zaglądać regularnie :)
Dzięki! :) Staram się jak mogę.
Pingback: Nowa Europa (według k-means) | Łukasz Prokulski
Pingback: MNIST dataset – sieci neuronowe, część 1 | Łukasz Prokulski
Fajny i rozbudowany artykuł! Zastanawia mnie natomiast, czy nie sensowniej było by użyć K najbliższych sąsiadów zamiast K-średnich ;) – no bo ten pierwszy nieco lepiej nadaje się do klasyfikacji. Ale w sumie to pewnie była kwestia wyboru :).
Dzięki!