Jest sobie taka strona – Kaggle.com – na której badacze danych mogą próbować swoich sił w różnych konkursach. Najczęściej chodzi o to, żeby z opublikowanych danych treningowych przewidzieć wyniki dla danych testowych.
Tak jest w przypadku konkursu NYC Taxi Trip Durration w którym uczestniczę. Chodzi pokrótce o to, żeby na podstawie informacji o kursach taksówek przewidzieć czas trwania podróży. Do dyspozycji mamy dane z pierwszego półrocza 2016 roku – prawie półtora miliona wierszy. Jeśli chcesz spróbować swoich sił albo po prostu sprawdzić opublikowany niżej kod – ściągnij dane ze strony konkursu (do tego wpisu wystarczy plik train.csv).
W tym poście nie pokażę rozwiązania i nie zbuduję modelu (można kilka zobaczyć na stronie konkursu, moje też), ale przejdziemy przez cały proces analizy danych, odpowiedniego ich czyszczenia (w nieco skróconej formie) i szukania ukrytych w nich informacji. Wpis raczej mało popularnonaukowy, ale może interesuje Cię gdzie nowojorczycy jeżdżą taksówkami?
Potrzebujemy tylko kilku pakietów, z czego większość dla jednej czy dwóch funkcji.
|
1 2 3 4 5 |
library(tidyverse) library(data.table) # dla szybkiego wczytywania plików library(lubridate) library(ggmap) library(geosphere) # dla policzenia odległości między punktami |
Plik z danymi wrzucamy do folderu data/, a później wczytujemy:
|
1 |
train <- fread("data/train.csv") |
Co my tutaj mamy?
|
1 |
glimpse(train) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
## Observations: 1,458,644 ## Variables: 11 ## $ id <chr> "id2875421", "id2377394", "id3858529", "id3... ## $ vendor_id <int> 2, 1, 2, 2, 2, 2, 1, 2, 1, 2, 2, 2, 2, 2, 2... ## $ pickup_datetime <chr> "2016-03-14 17:24:55", "2016-06-12 00:43:35... ## $ dropoff_datetime <chr> "2016-03-14 17:32:30", "2016-06-12 00:54:38... ## $ passenger_count <int> 1, 1, 1, 1, 1, 6, 4, 1, 1, 1, 1, 4, 2, 1, 1... ## $ pickup_longitude <dbl> -73.98215, -73.98042, -73.97903, -74.01004,... ## $ pickup_latitude <dbl> 40.76794, 40.73856, 40.76394, 40.71997, 40.... ## $ dropoff_longitude <dbl> -73.96463, -73.99948, -74.00533, -74.01227,... ## $ dropoff_latitude <dbl> 40.76560, 40.73115, 40.71009, 40.70672, 40.... ## $ store_and_fwd_flag <chr> "N", "N", "N", "N", "N", "N", "N", "N", "N"... ## $ trip_duration <int> 455, 663, 2124, 429, 435, 443, 341, 1551, 2... |
Kolejne cechy to:
- id – ID konkretnego kursu
- vendor_id – ID korporacji taksówkarskiej (są dwie)
- pickup_datetime – data i czas rozpoczęcia kursu
- dropoff_datetime – data i czas zakończenia kursu (oczywiście nie ma tego pola w danych testowych)
- passenger_count – liczba pasażerów
- pickup_longitude oraz pickup_latitude – lokalizacja (współrzędne geograficzne) miejsca rozpoczęcia kursu
- dropoff_longitude oraz dropoff_latitude – miejsce zakończenia kursu. W realnym świecie ta informacja może nie być dostępna w momencie rozpoczęcia kursu – jednak na potrzeby konkursu pozostawiono ją w danych. Ciekawe było by przygotowanie modelu bez tej informacji…
- store_and_fwd_flag – flaga mówiąca o tym czy dane o kursie były przechowywane w pamięci pojazdu przed wysłaniem do sieci taksówkarskiej kiedy pojazd nie miał połączenia z serwerem; w niniejszym wpisie odpuścimy sobie analizę tego pola
- trip_duration – czas trwania podróży (w sekundach). To coś co należy znaleźć dla danych testowych
Na początek pozbędziemy się wszystkich danych odstających.
Zaczniemy od lokalizacji. Czy miejsca są w miarę zwarte czy też mocno rozproszone? Narysujemy histogramy dla każdej ze współrzędnych i sprawdzimy. Wszystkie miejsca powinny być skupione w jakimś ograniczonym terenie.
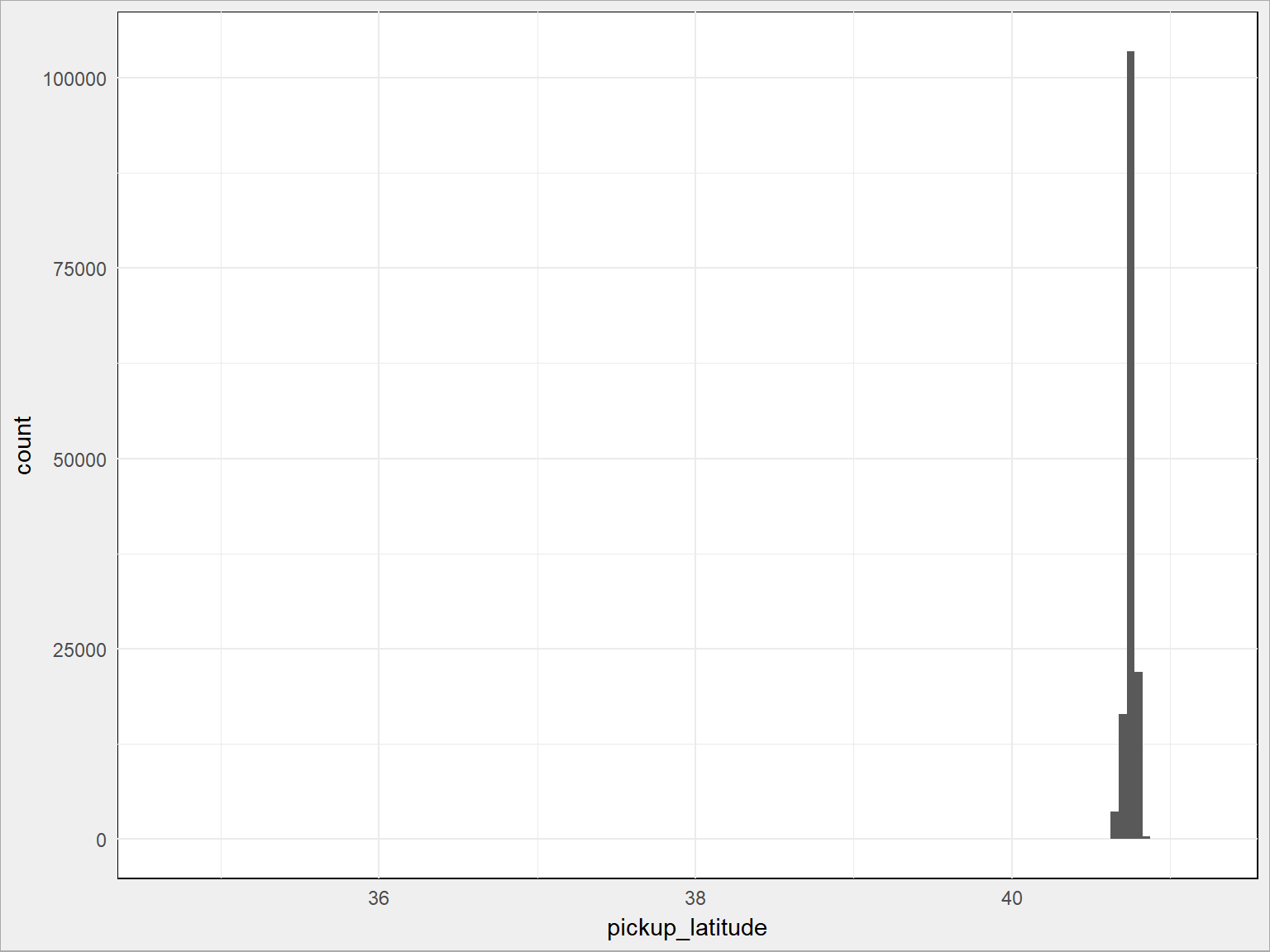
Sprawdźmy szerokość geograficzną miejsc startowych kursu (weźmy tylko 10% danych, żeby narysowało się to szybciej):
|
1 2 3 4 |
train %>% sample_frac(size = 0.1) %>% # 10% danych ggplot() + geom_histogram(aes(pickup_latitude), binwidth = 0.05) |
A teraz długość geograficzną tych miejsc:
|
1 2 3 4 |
train %>% sample_frac(size = 0.1) %>% ggplot() + geom_histogram(aes(pickup_longitude), binwidth = 0.05) |
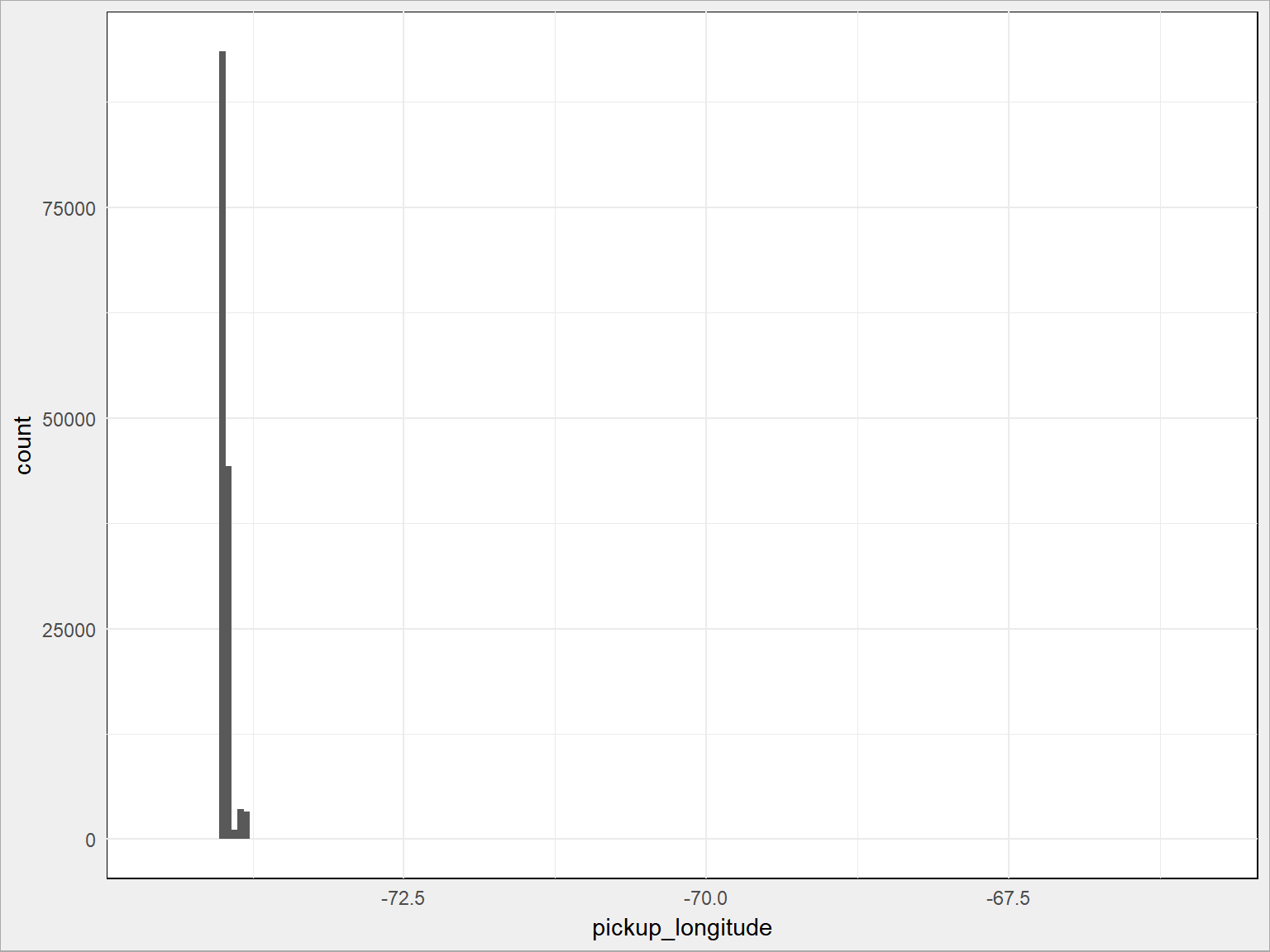
Jest tak jak zakładaliśmy, z małymi wyjątkami (osie poziome na obu wykresach byłyby krótsze, gdyby nie odstające punkty). Widać to zresztą po podsumowaniach odpowiednich kolumn:
|
1 2 |
# szerokość geograficzna summary(train$pickup_latitude) |
|
1 2 |
## Min. 1st Qu. Median Mean 3rd Qu. Max. ## 34.36 40.74 40.75 40.75 40.77 51.88 |
|
1 2 |
# długość geograficzna summary(train$pickup_longitude) |
|
1 2 |
## Min. 1st Qu. Median Mean 3rd Qu. Max. ## -121.93 -73.99 -73.98 -73.97 -73.97 -61.34 |
Dla szerokości mamy środek w punkcie 40.75 i pojedyncze punkty o około 10 stopni kątowych na północ i na południe (1 stopień szerokości to – jak wiemy z geografii i geometrii – 20 tys. km dla 180 stopni = 111.1 km), czyli o jakieś tysiąc kilometrów od środka! To na pewno błędy. Dla długości geograficznej mamy jeszcze większe różnice.
Metodą przybliżeń (odpowiedniego filtrowana z jednej i drugiej strony) histogramu uzyskałem granice obszaru NYC:
- dla szerokości – od 40.6 stopnia do 40.9 stopnia
- dla długości – od 74.25 stopnia do 73.75 stopnia (na półkuli zachodniej, stąd minusy)
Mamy 1458644 wierszy wszystkich danych. Po przefiltrowaniu (w tych samych granicach miejsce rozpoczęcia i zakończenia kursu):
|
1 2 3 4 5 |
train <- train %>% filter(pickup_latitude >= 40.6 & pickup_latitude <= 40.9) %>% filter(pickup_longitude >= -74.25 & pickup_longitude <= -73.75) %>% filter(dropoff_latitude >= 40.6 & dropoff_latitude <= 40.9) %>% filter(dropoff_longitude >= -74.25 & dropoff_longitude <= -73.75) |
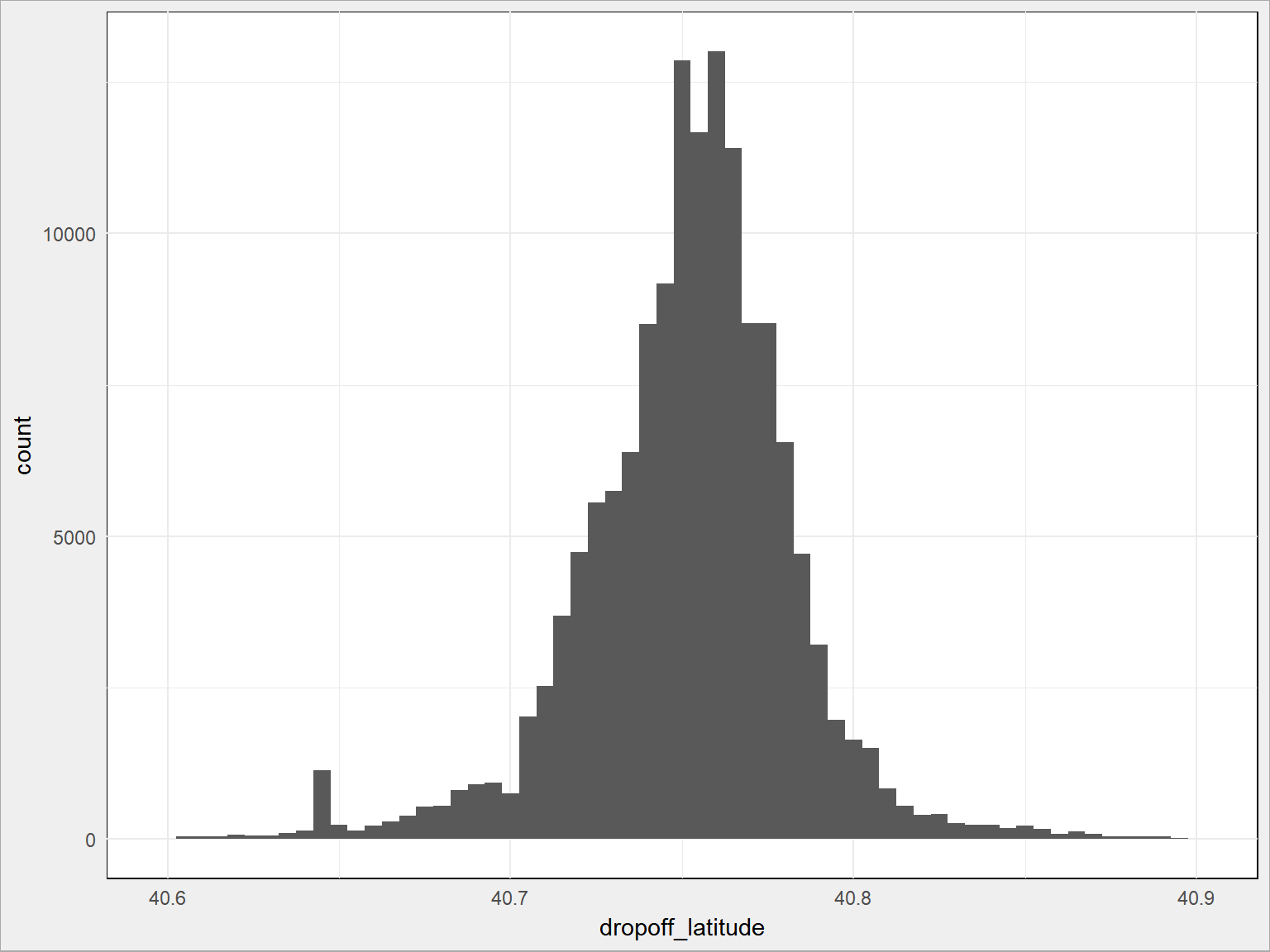
zostaje nam 1454759 wierszy. Nie straciliśmy wiele (jakieś 4 tysiące, jak dobrze liczę? to jest około 0.25% danych). Zobaczmy jak teraz wygląda rozkład. Żeby było inaczej – tym razem dla zakończeń kursu (też na 10% danych, tym razem z 10-krotnie większą dokładnością)
- szerokość geograficzna:
|
1 2 3 4 |
train %>% sample_frac(size = 0.1) %>% ggplot() + geom_histogram(aes(dropoff_latitude), binwidth = 0.005) |
- i długość geograficzna:
|
1 2 3 4 |
train %>% sample_frac(size = 0.1) %>% ggplot() + geom_histogram(aes(dropoff_longitude), binwidth = 0.005) |
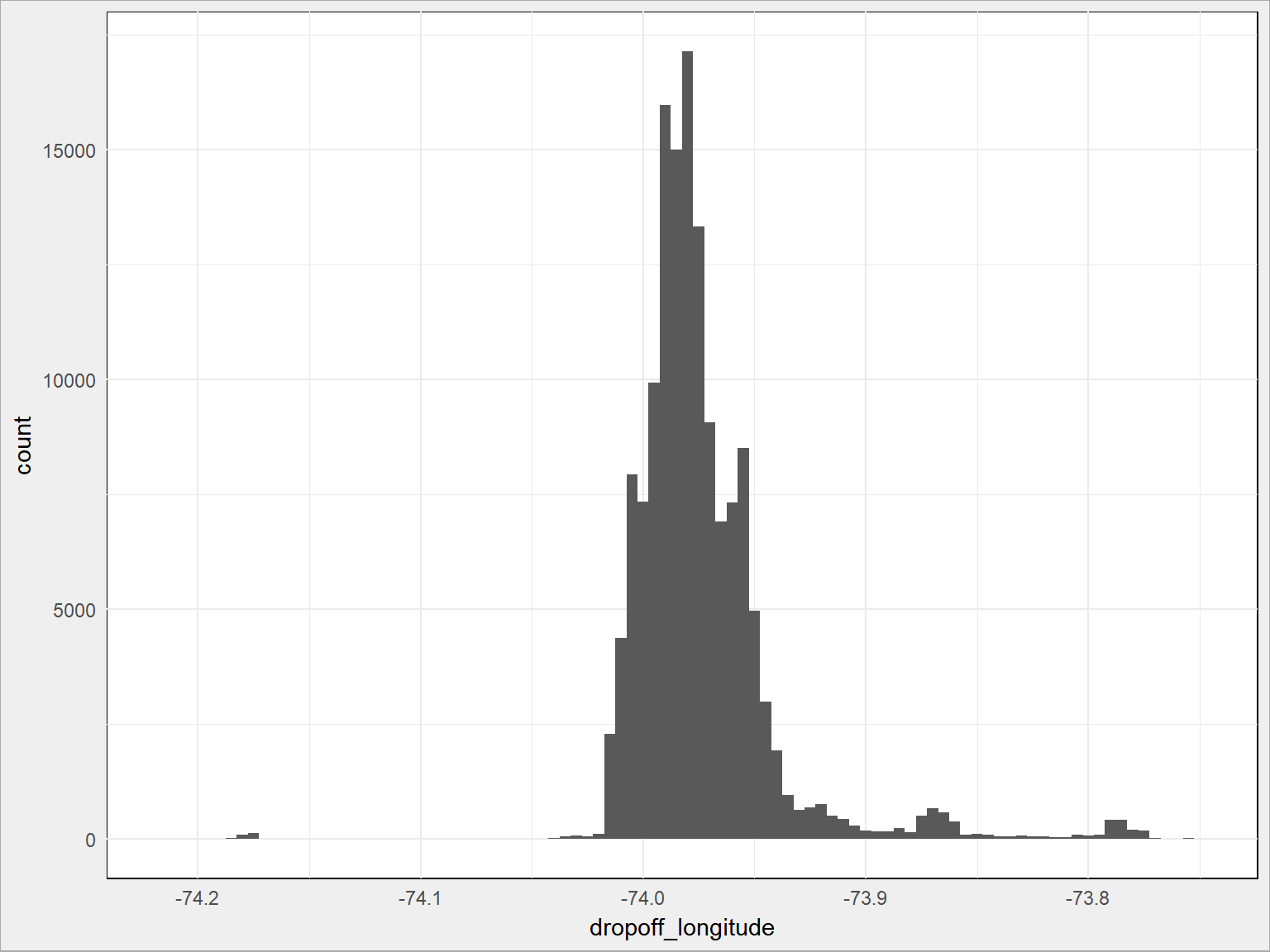
Dużo lepiej, prawda? Co to są te najpopularniejsze miejsca, wiecie? Skąd odjeżdżają taksówki? Zobaczmy na mapie: (znowu – 10% danych)
|
1 2 3 4 5 6 7 8 9 10 11 |
# NYC map ny_map <- get_map(location = c(mean(train$pickup_longitude), mean(train$pickup_latitude)), zoom = 11) ggmap(ny_map, darken = 0.7) + geom_point(data = train %>% sample_frac(size = 0.1), aes(pickup_longitude, pickup_latitude), alpha = 0.05, size = 0.1, color = "red") + theme(axis.text.x = element_blank(), axis.text.y = element_blank()) + labs(x = "", y = "") |
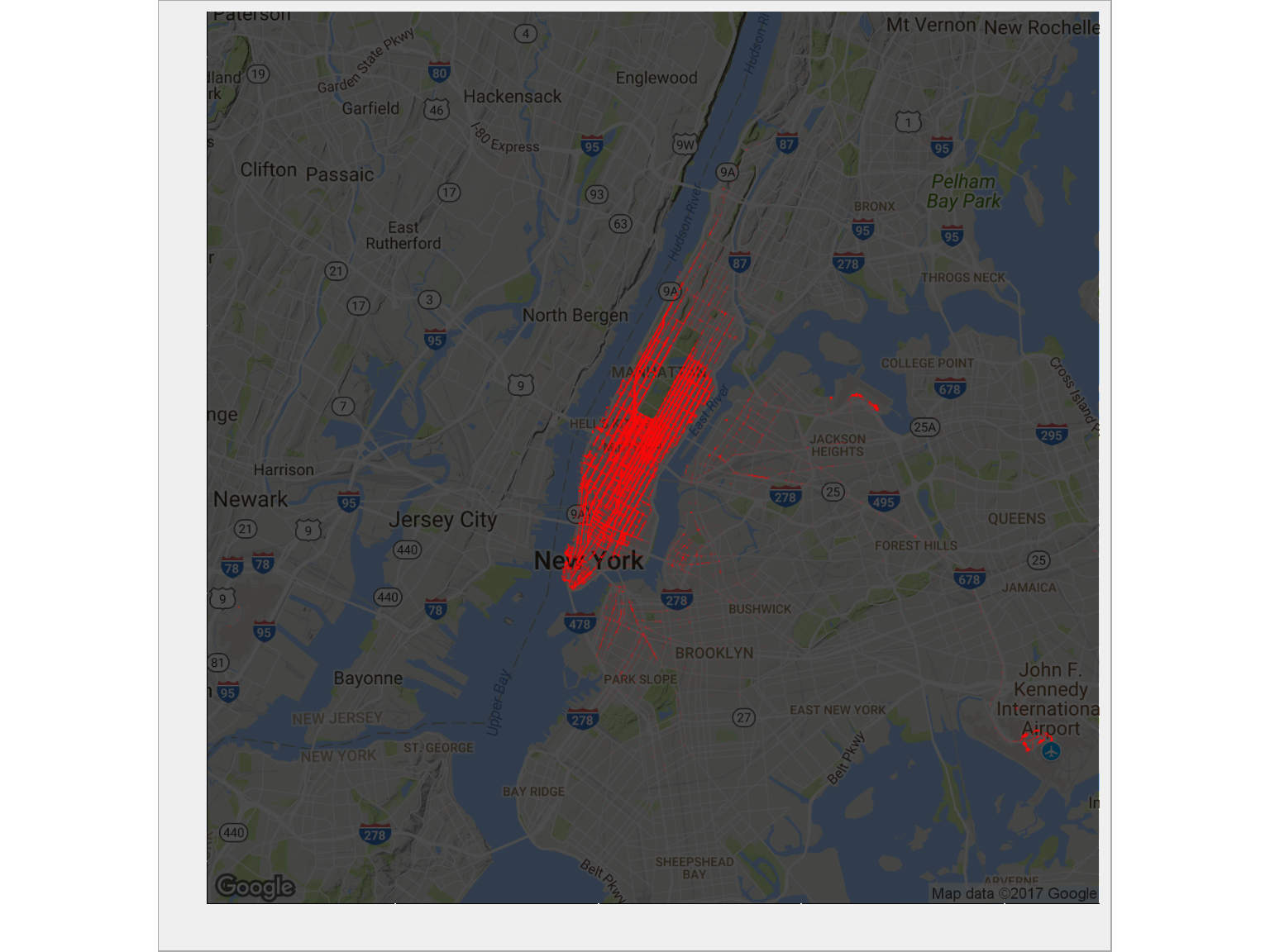
A dokąd przyjeżdżają?
|
1 2 3 4 5 6 |
ggmap(ny_map, darken = 0.7) + geom_point(data = train %>% sample_frac(size = 0.1), aes(dropoff_longitude, dropoff_latitude), alpha = 0.05, size = 0.1, color = "green") + theme(axis.text.x = element_blank(), axis.text.y = element_blank()) + labs(x = "", y = "") |
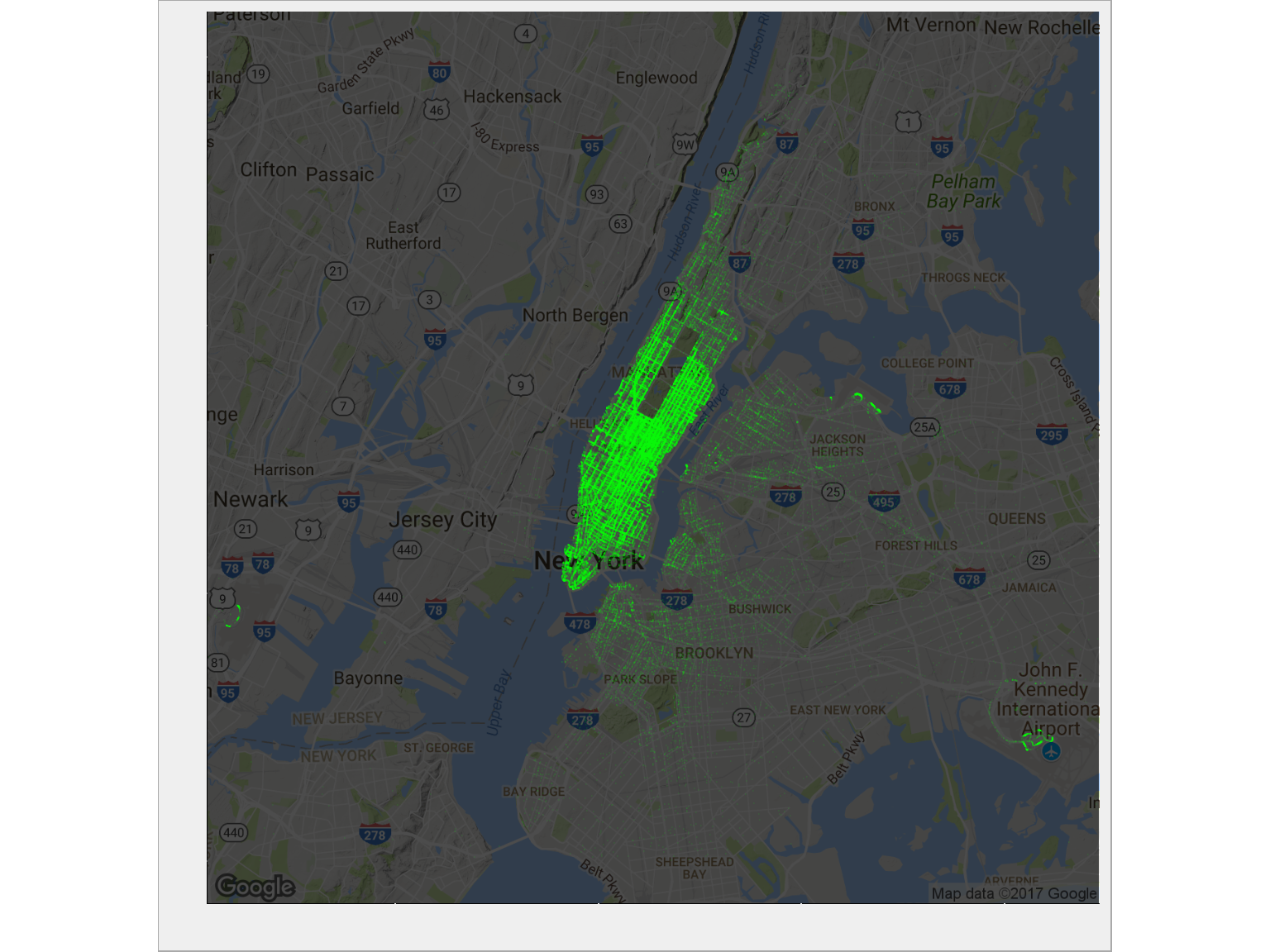
To jest moment w którym słyszysz Błękitną rapsodię i widzisz początek jednego z moich ulubionych filmów Woody Allena. Tego nie można nie znać… niecałe 4 minuty, możesz poświęcić na obejrzenie:
Manhattan. Po prostu . Tam jest największy ruch. Widać wyraźnie pusty prostokąt Central Parku. Widać też skupisko w prawym dolnym rogu. Dojdziemy z czasem do tego czym ono jest (nie znam Nowego Jorku, więc nie rozpoznaję. Rozpoznaję Kraków i Warszawę :).
Czas na drugie filtrowanie. Sprawdźmy najpierw jak wygląda rozkład czasu podróży:
|
1 |
summary(train$trip_duration) |
|
1 2 |
## Min. 1st Qu. Median Mean 3rd Qu. Max. ## 1 397 661 956 1072 3526282 |
|
1 2 3 4 5 |
train %>% sample_frac(size = 0.05) %>% # tylko 5% danych ggplot() + geom_histogram(aes(trip_duration), binwidth = 5) + # w blokach po 5 sekund scale_y_sqrt() # spłaszczenie osi Y, żeby szpilka nie była taka ostra :) |
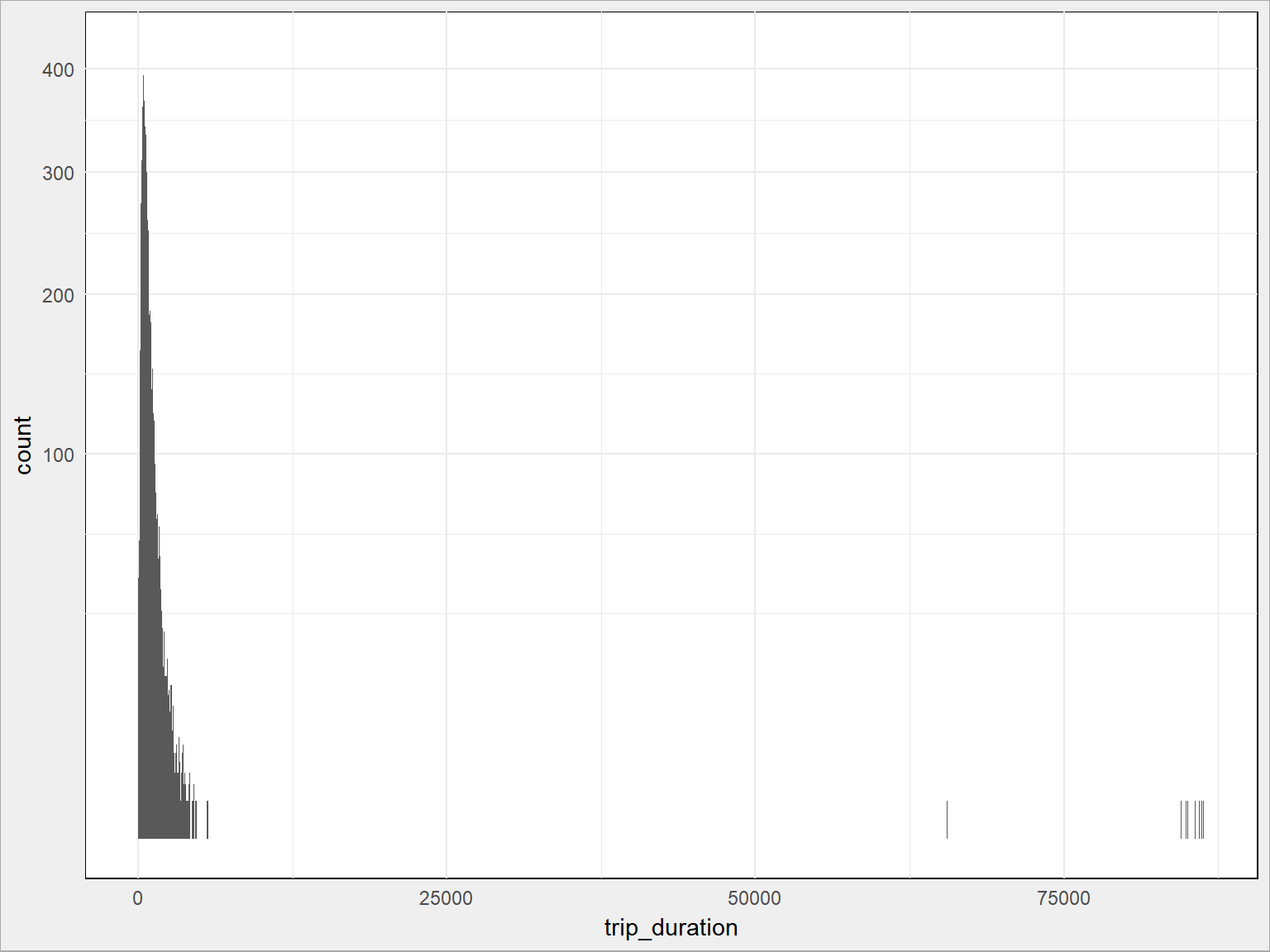
Widać, że są jakieś minimalne (mniej niż 30 sekund w taksówce to dość dziwaczne, podobnie więcej niż – powiedzmy – dwie godziny (7200 sekund)). Obetnijmy właśnie tak dane.
Z 1454759 wierszy…
|
1 2 |
train <- train %>% filter(trip_duration <= 7200, trip_duration >= 30) |
zostaje nam 1447865 – znowu usunęliśmy niewiele (jakieś 0.5%). Wszystko po to, żeby wartości odstające nie wpływały na model.
Teraz rozkład czasu podróży wygląda tak:
|
1 2 3 4 5 |
train %>% sample_frac(size = 0.1) %>% ggplot() + geom_histogram(aes(trip_duration), binwidth = 5) + scale_y_sqrt() |
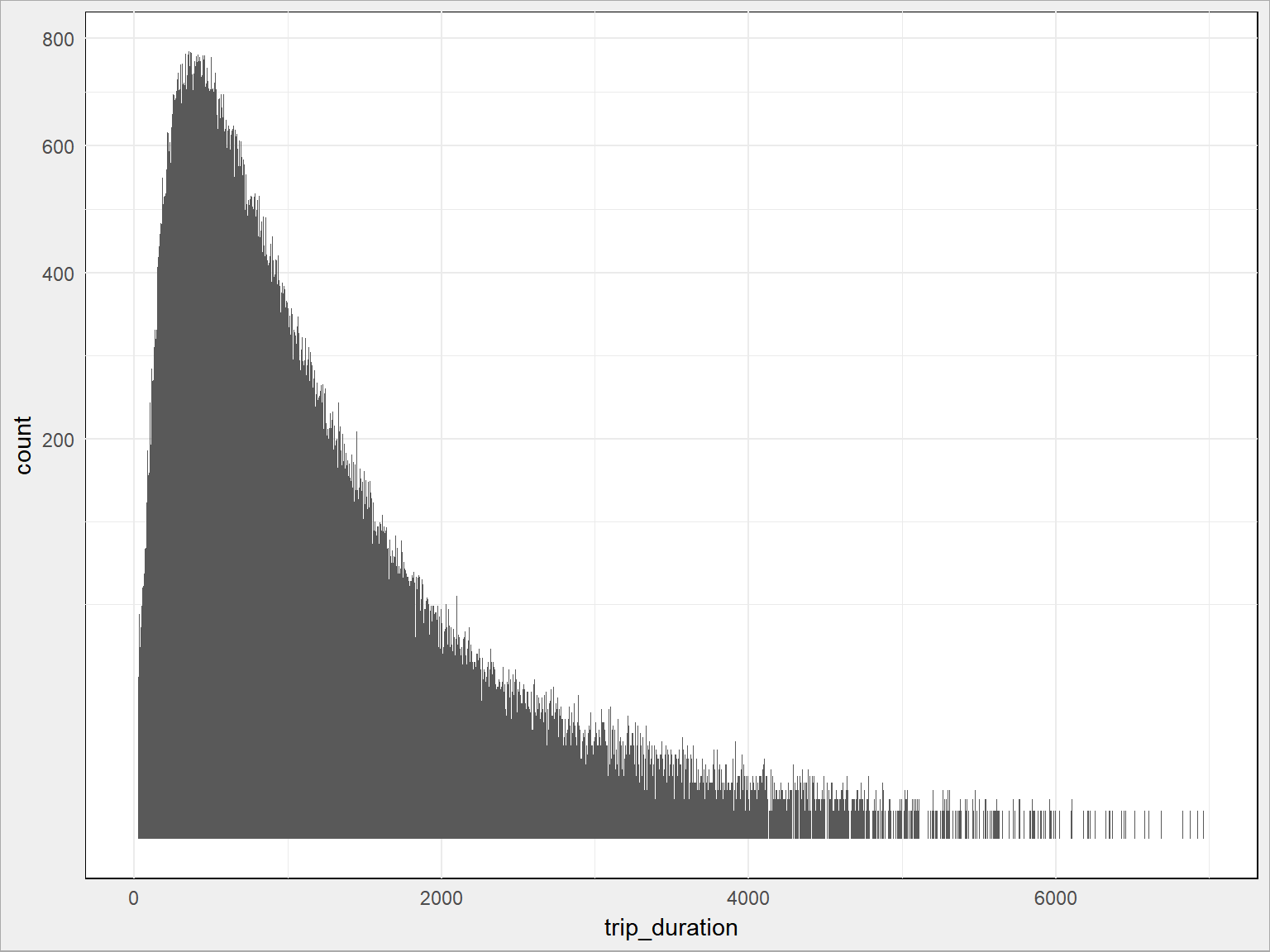
Można było obciąć przy 6000 sekundach, nawet może i 5000?
Na razie mamy tylko odrzucone wartości dziwne – poza miastem i podróże zbyt długie (oraz zbyt krótkie). Niczego nie wiemy o charakterze zmian czasu podróży – czy od czegoś zależy? A przecież to czas podróży mamy prognozować!
Najpierw przygotujmy informacje o dacie, tak aby pozwalały na różne przekroje. Nie mamy w danych testowych informacji o momencie zakończeniu kursu, więc odpuścimy sobie ją w danych treningowych. Zresztą data i godzina zakończenia kursu będzie prawie jednakowa z porą jego rozpoczęcia. To chyba niewiele wniesie do modelu.
|
1 2 3 4 5 6 7 |
train$pickup_datetime <- ymd_hms(train$pickup_datetime) train <- train %>% mutate(pickup_hour = hour(pickup_datetime), pickup_day = day(pickup_datetime), pickup_month = month(pickup_datetime), pickup_weekday = wday(pickup_datetime)) |
Czy liczba kursów zależy od miesiąca?
|
1 2 3 4 5 6 |
train %>% count(pickup_month) %>% ggplot() + geom_bar(aes(pickup_month, n, fill = pickup_month), stat = "identity", color = "black", show.legend = FALSE) + scale_x_continuous(breaks = 1:6) |
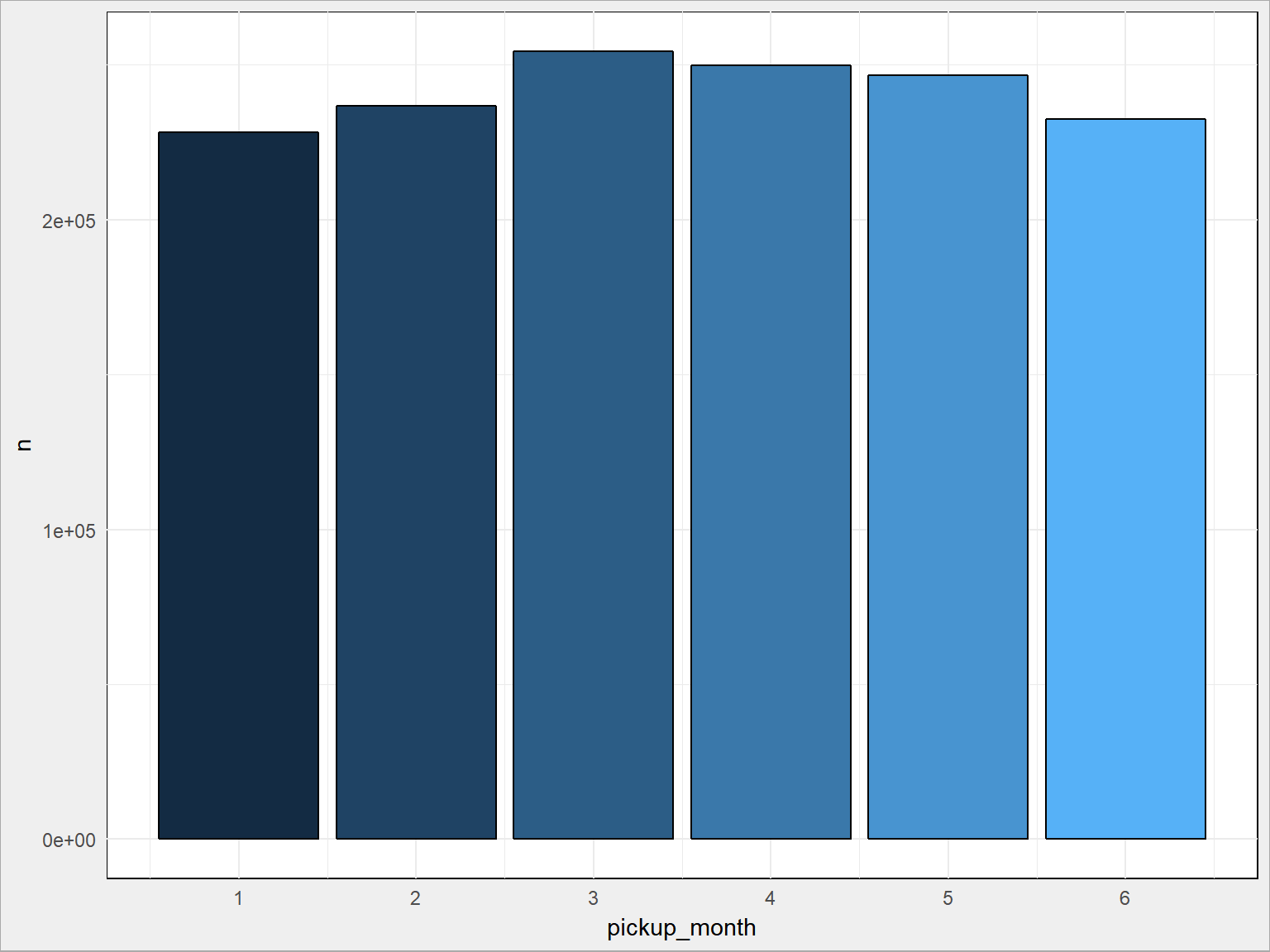
No nie bardzo, a gdyby jeszcze przeskalować ją ilością dni w miesiącu to już pewnie wcale.
A od dnia tygodnia? Najpierw zmienimy numerację dni tygodnia. Pakiet lubridate uznaje niedzielę za początek tygodnia (dzień numer 1) i sobotę (dzień numer 7) za koniec. Musimy to “zrolować” nieco:
|
1 2 3 4 5 6 7 8 9 |
# najpierw zamienimy wartości na factor-y w odpowiedniej kolejności # (od poniedziałku do niedzieli) # i nadamy im nowe labelki train$pickup_weekday <- factor(train$pickup_weekday, levels = c(2, 3, 4, 5, 6, 7, 1), labels = c("1", "2", "3", "4", "5", "6", "7")) # a teraz z factor wracamy do liczb całkowitych: train$pickup_weekday <- as.integer(as.character(train$pickup_weekday)) |
Teraz pierwszy dzień tygodnia to poniedziałek. Więc jak wygląda rozkład ilości kursów w poszczególne dni?
|
1 2 3 4 5 6 |
train %>% count(pickup_weekday) %>% ggplot() + geom_bar(aes(pickup_weekday, n, fill = pickup_weekday), stat = "identity", color = "black", show.legend = FALSE) + scale_x_continuous(breaks = 1:7) |
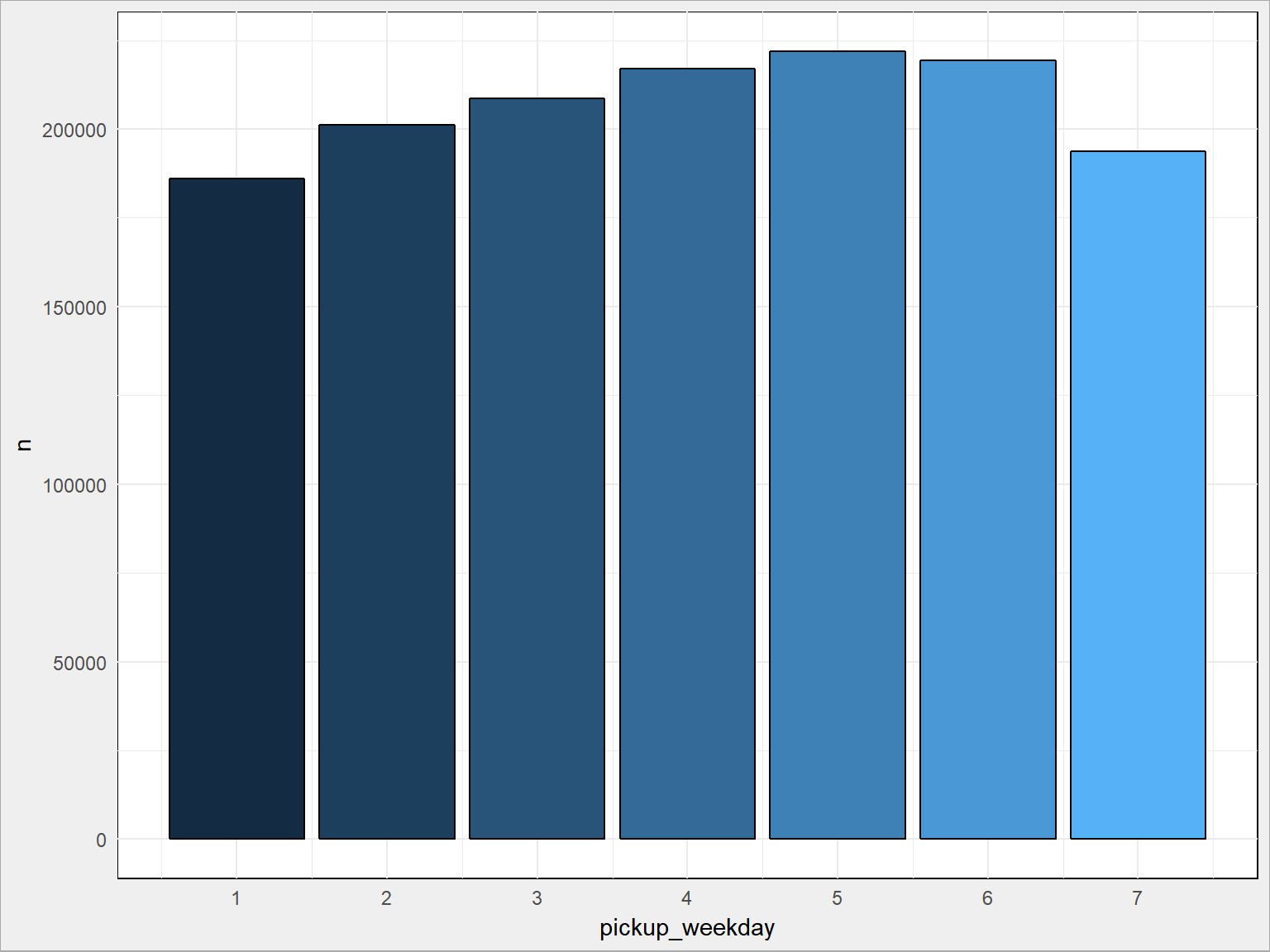
Szczerze mówiąc minimum poniedziałkowe nieco dziwi… Pytanie ile było poniedziałków? Może lepiej liczyć średnią? Sprawdźcie.
Zobaczmy rozkład po godzinach:
|
1 2 3 4 5 |
train %>% count(pickup_hour) %>% ggplot() + geom_bar(aes(pickup_hour, n, fill = pickup_hour), stat = "identity", color = "black", show.legend = FALSE) |
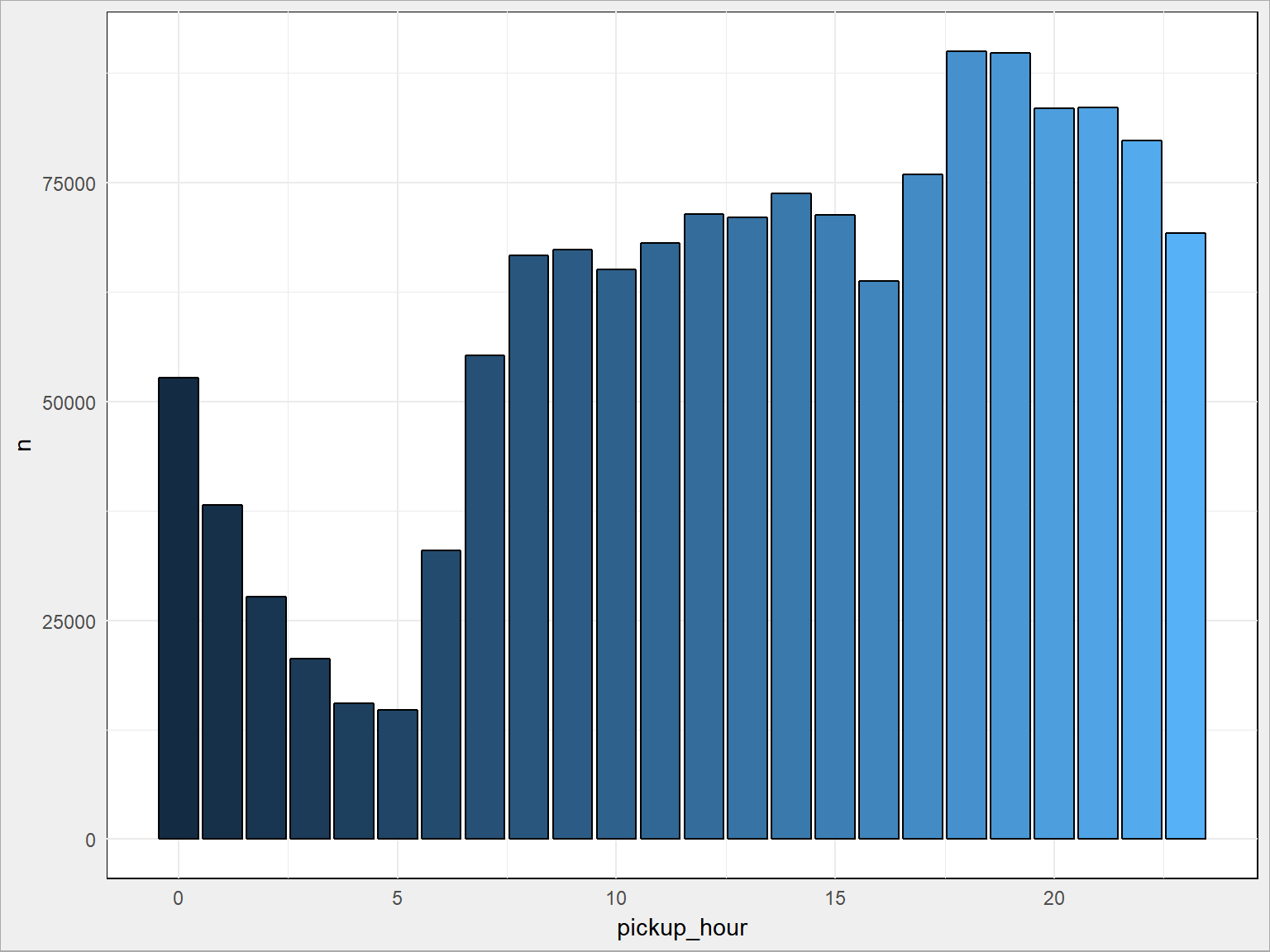
To już wygląda sensownie – minimum nad ranem, w miarę umiarkowanie w ciągu dnia i szczyt popołudniowy (po pracy, po wieczornych rozrywkach). Czy to się zmienia w ciągu tygodnia?
|
1 2 3 4 5 6 7 |
train %>% count(pickup_weekday, pickup_hour) %>% ggplot() + geom_tile(aes(pickup_weekday, pickup_hour, fill = n), color = "white") + scale_fill_gradient(low = "darkred", high = "yellow") + scale_x_continuous(breaks = 1:7) + scale_y_continuous(breaks = seq(0, 24, 3), trans = "reverse") |
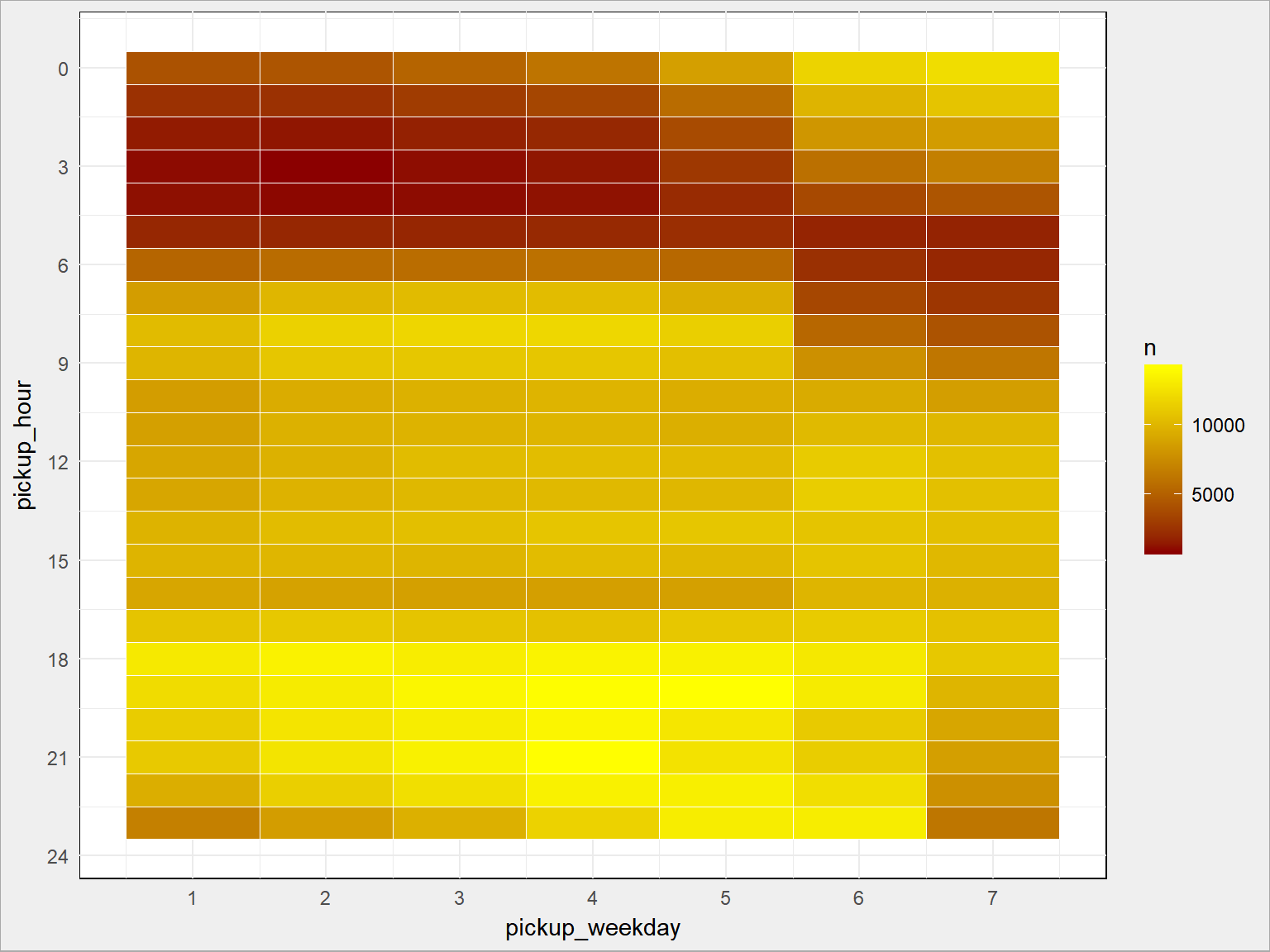
Widać górkę popołudnowo-wieczorną przesuniętą na później w weekend, a także więcej podróży w weekend w okolicach północy. Ładnie to widać też na innego rodzaju wykresie:
|
1 2 3 4 5 6 |
train %>% count(pickup_weekday, pickup_hour) %>% ggplot() + geom_line(aes(pickup_hour, n, color=as.factor(pickup_weekday)), size = 1) + scale_x_continuous(breaks = seq(0, 24, 2)) + labs(color = "weekday") |
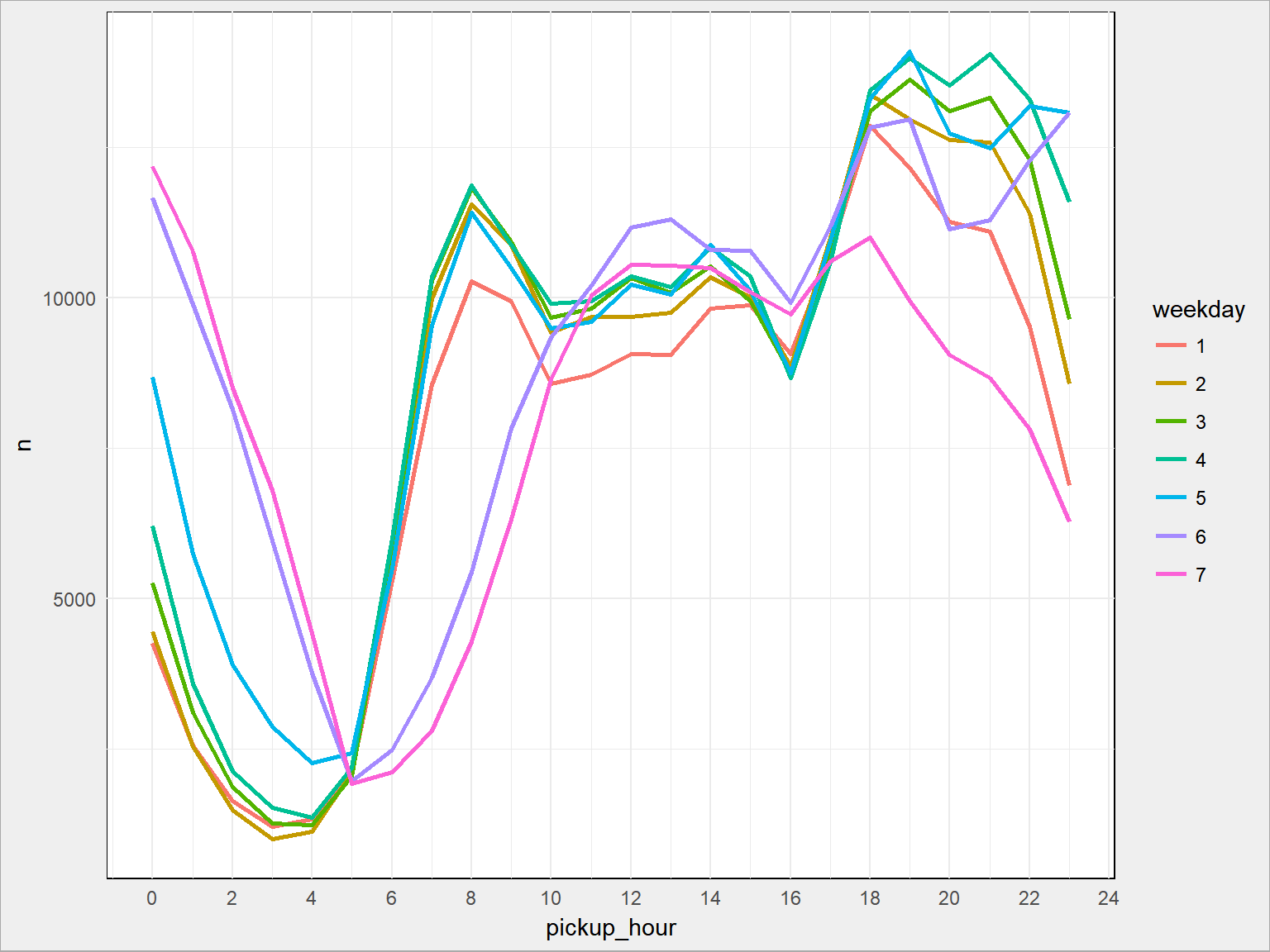
na którym widać też większą liczbę przejazdów w okolicach 8 rano.
Zobaczmy jeszcze układ dzień po dniu (bo jest ciekawy):
|
1 2 3 4 5 6 7 |
train %>% count(pickup_month, pickup_day) %>% ggplot() + geom_tile(aes(pickup_month, pickup_day, fill=n), color = "white") + scale_fill_gradient(low = "darkred", high = "yellow") + scale_x_continuous(breaks = 1:6) + scale_y_continuous(breaks = seq(1, 31, 3), trans = "reverse") |
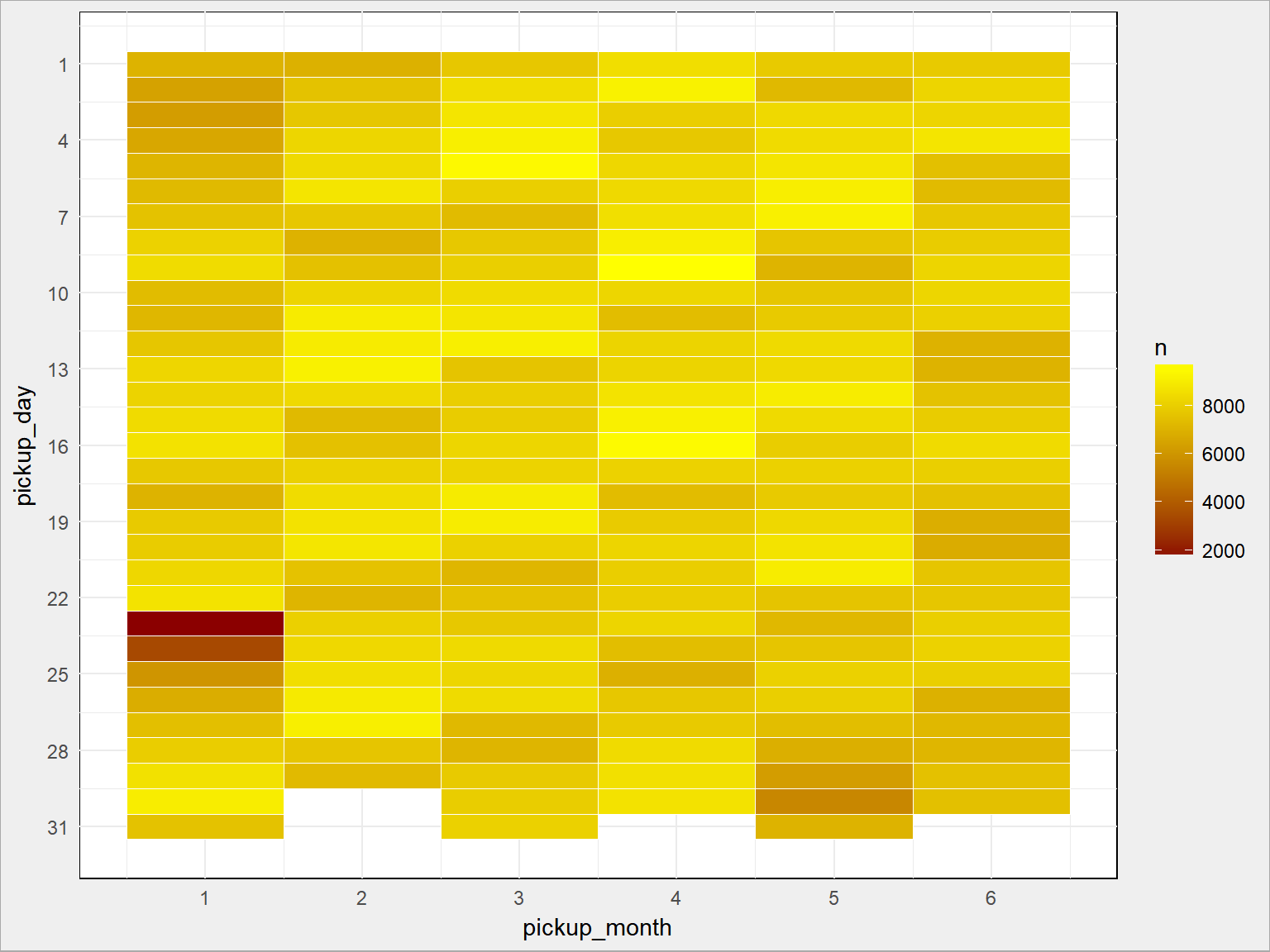
Coś zwróciło Waszą uwagę? Jest cyklicznie, co siedem dni. Ale w dniach 23 i 24 stycznia 2016 roku stało się coś dziwnego. Jak odrzucimy te dni mamy:
|
1 2 3 4 5 6 7 8 9 10 11 |
train %>% mutate(remove = ifelse(pickup_month == 1 & pickup_day == 23, 1, 0)) %>% filter(remove == 0) %>% mutate(remove = ifelse(pickup_month == 1 & pickup_day == 24, 1 , 0)) %>% filter(remove == 0) %>% count(pickup_month, pickup_day) %>% ggplot() + geom_tile(aes(pickup_month, pickup_day, fill=n), color = "white") + scale_fill_gradient(low = "darkred", high = "yellow") + scale_x_continuous(breaks = 1:6) + scale_y_continuous(breaks = seq(1, 31, 3), trans = "reverse") |
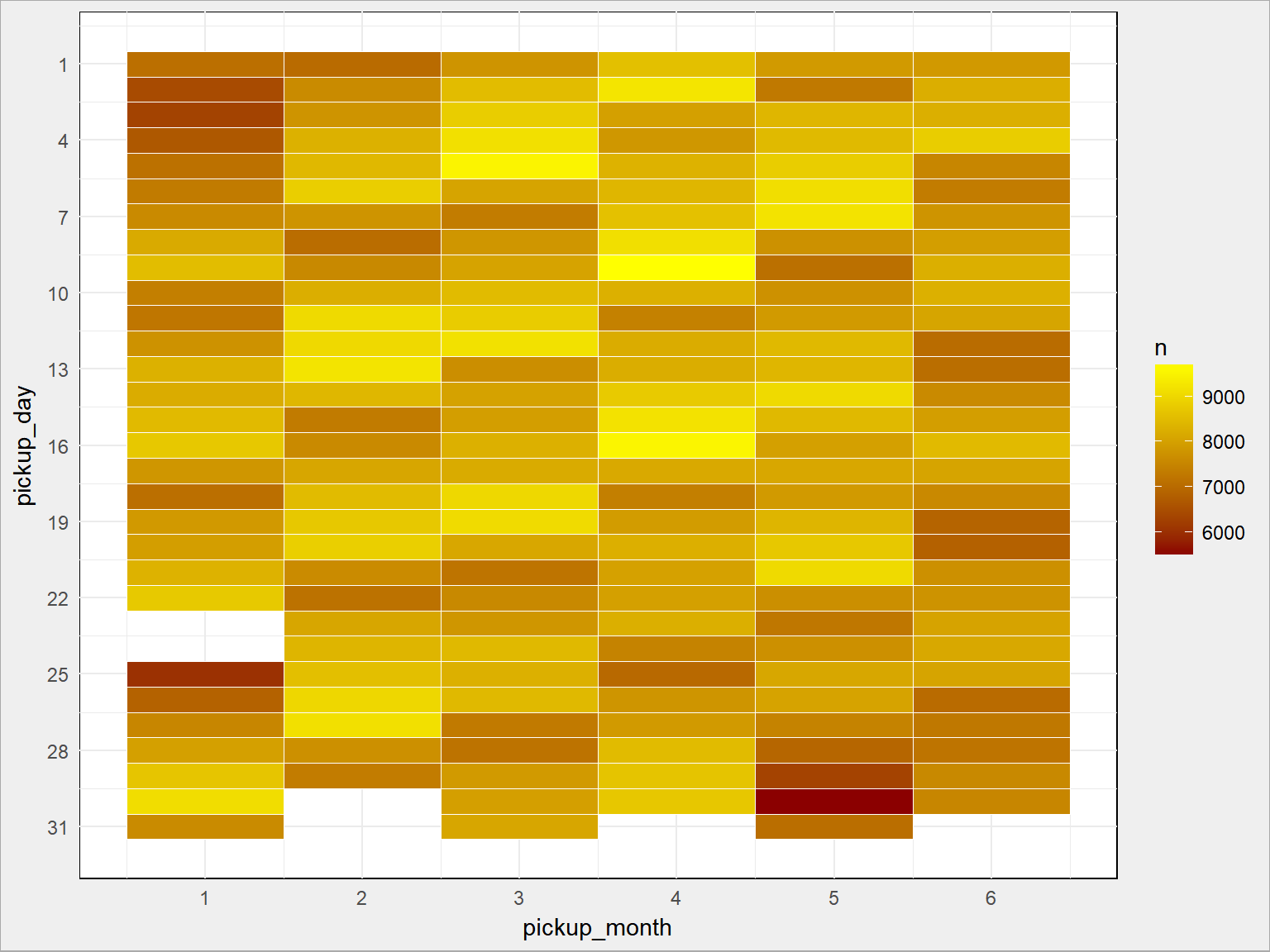
…o wiele bardziej widoczną tygodniową cykliczność. Jakby to było wykres typu calendar plot to byłoby jeszcze ładniej.
Ale wróćmy do tego 23-24 stycznia. Trzeba googlać. Albo pamiętać. Tej nocy nad Nowym Jorkiem przeszła ogromna śnieżyca (ogromna w wersji amerykańskiej – więcej krzyku niż prawdziwej zimy). Służby zapowiadały kataklizm, chyba wstrzymany był ruch na ulicach. Googlajcie po szczegóły.
Możemy sprawdzić jak długo (tym razem czas w minutach) trwa podróż taksówką w zależności od dnia tygodnia i pory dnia:
|
1 2 3 4 5 6 7 8 9 10 11 |
train %>% group_by(pickup_weekday, pickup_hour) %>% summarise(trip_duration = mean(trip_duration)/60) %>% ungroup() %>% ggplot() + geom_line(aes(pickup_hour, trip_duration, group = pickup_weekday, color = as.factor(pickup_weekday)), size = 1) + scale_x_continuous(breaks = seq(0, 24, 3)) + labs(color = "weekday") |
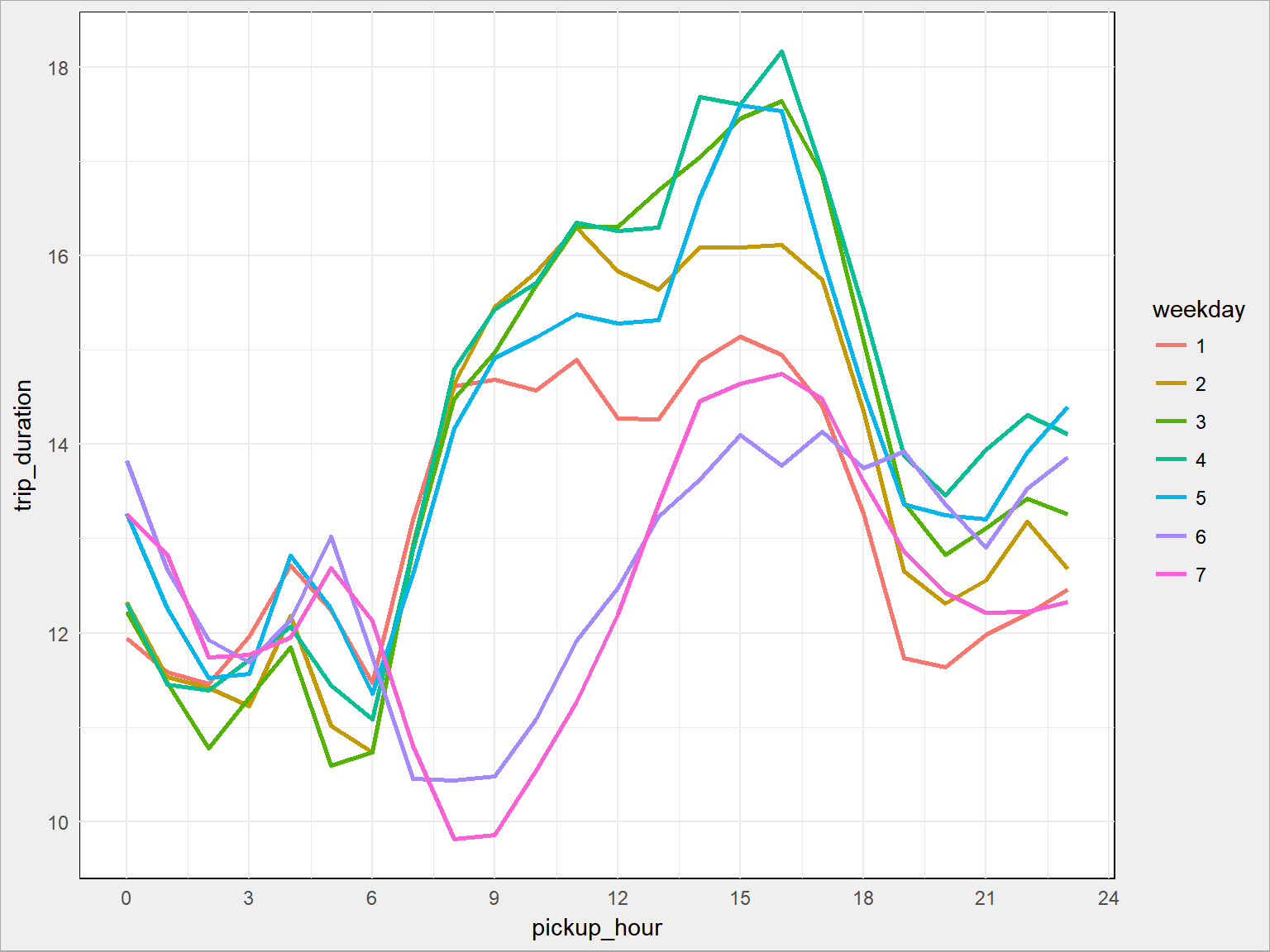
W ciągu dnia roboczego podróże są stosunkowo krótkie – około 15-16 minut. Najkrótsze są przejazdy weekendowe.
Wiemy coś o czasie, mamy położenia początku i końca – możemy zatem policzyć odległości pomiędzy punktami. Mając czas i odległość możemy policzyć prędkość. Do dzieła zatem.
Najpierw odległości (po sferze – używając distHaversine(), można w sumie liczyć zwykłą odległość euklidesową – w ramach miasta krzywizna Ziemi nie będzie mieć dużego znaczenia), a przy okazji kierunek (azymut – korzystając z funkcji bearing()). Obie funkcje pochodzą z pakietu geosphere. Ten kawałek kodu wykonuje się długo; przeliczone dane warto więc zapisać i później z nich korzystać żeby nie liczyć wielokrotnie.
|
1 2 3 4 5 6 7 |
train <- train %>% rowwise() %>% mutate(trip_distance = distHaversine(c(pickup_longitude, pickup_latitude), c(dropoff_longitude, dropoff_latitude))/1000) %>% mutate(bearing = bearing(c(pickup_longitude, pickup_latitude), c(dropoff_longitude, dropoff_latitude))) %>% ungroup() |
Zobaczmy jak wygląda rozkład długości podróży:
|
1 2 3 |
train %>% ggplot() + geom_histogram(aes(trip_distance), binwidth = 0.25) |
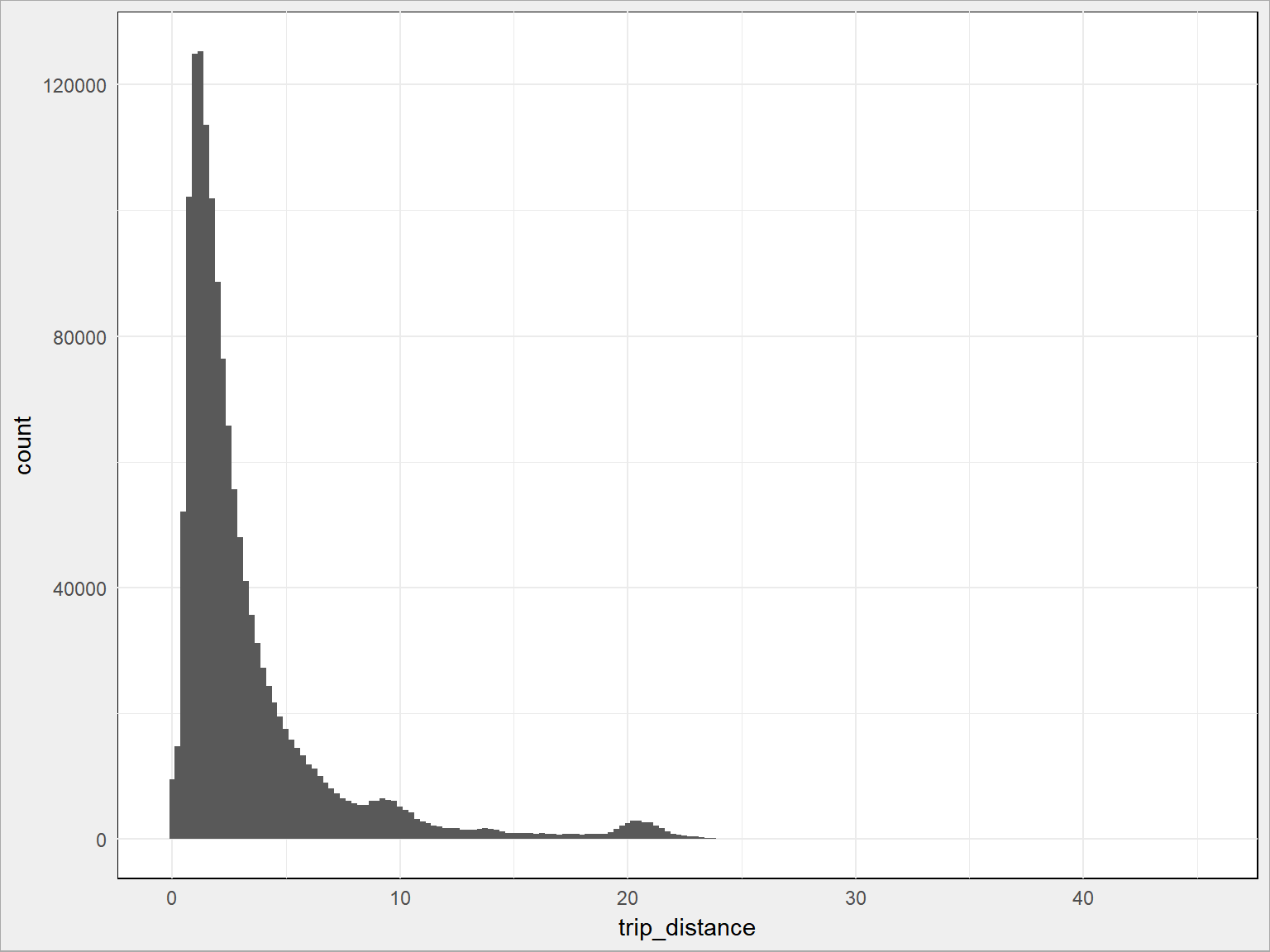
Widzimy górki w okolicach 9-10 kilometrów oraz nieco powyżej 20. Wszystko się wyjaśni :)
A jak wygląda rozkład azymutów?
|
1 2 3 4 5 6 |
train %>% sample_frac(size = 0.1) %>% mutate(bearing = round(bearing)) %>% count(bearing) %>% ggplot() + geom_bar(aes(bearing, n), stat = "identity") |
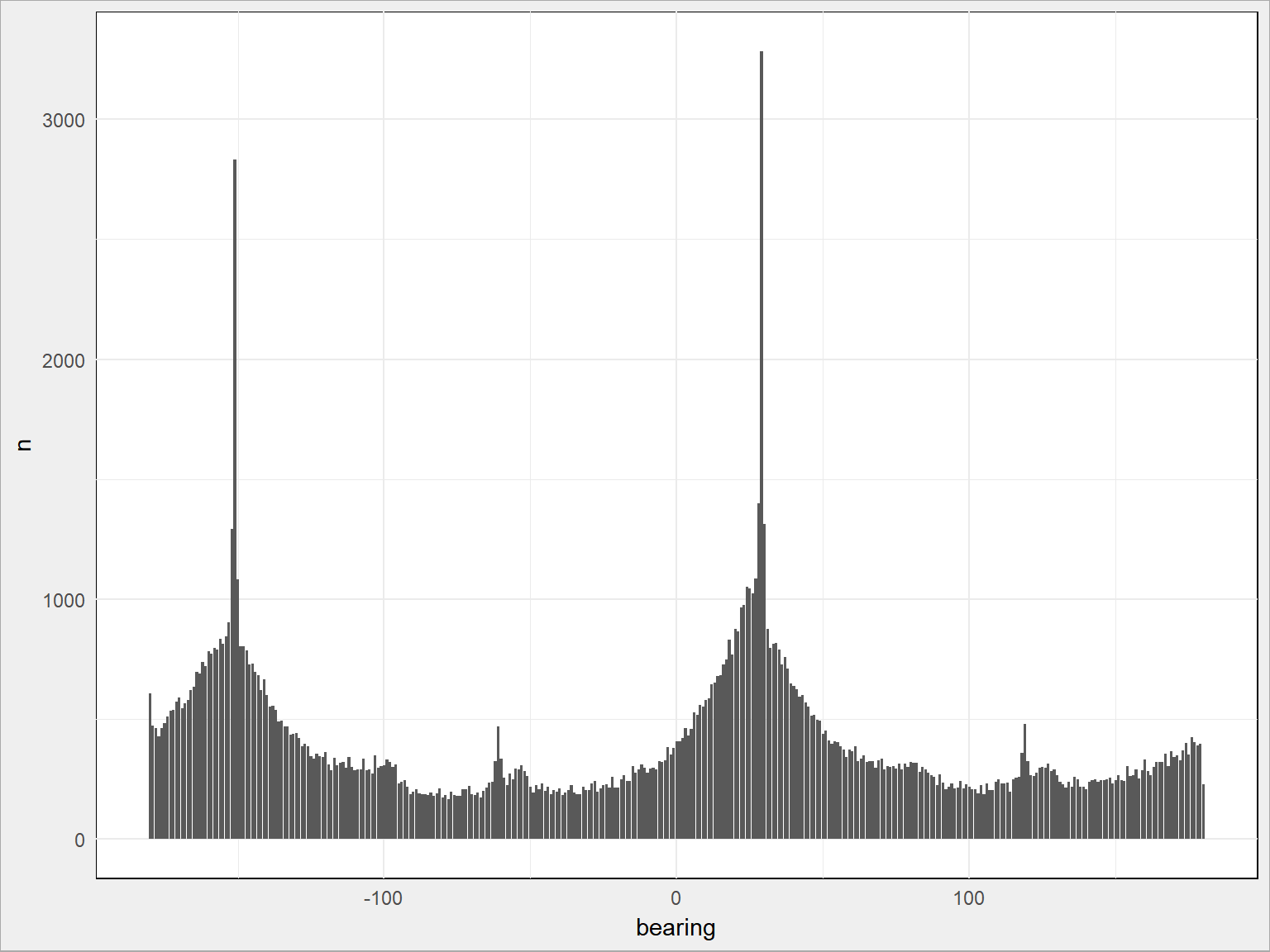
Widzimy dwa piki:
|
1 2 3 4 5 |
train %>% sample_frac(size = 0.1) %>% mutate(bearing = round(bearing)) %>% count(bearing) %>% top_n(2, wt = n) |
|
1 2 3 4 5 |
## # A tibble: 2 x 2 ## bearing n ## <dbl> <int> ## 1 -151 2822 ## 2 29 3316 |
Zobaczmy jakim podróżom to odpowiada:
|
1 2 3 4 5 6 7 8 9 10 11 |
train %>% mutate(bearing = round(bearing)) %>% filter(bearing %in% c(-151, 29)) %>% ggplot() + # czerwone skąd? geom_point(aes(pickup_longitude, pickup_latitude), size = 0.1, alpha = 0.1, color = "red") + # zielone dokąd? geom_point(aes(dropoff_longitude, dropoff_latitude), size = 0.1, alpha = 0.1, color = "green") + facet_wrap(~bearing) |
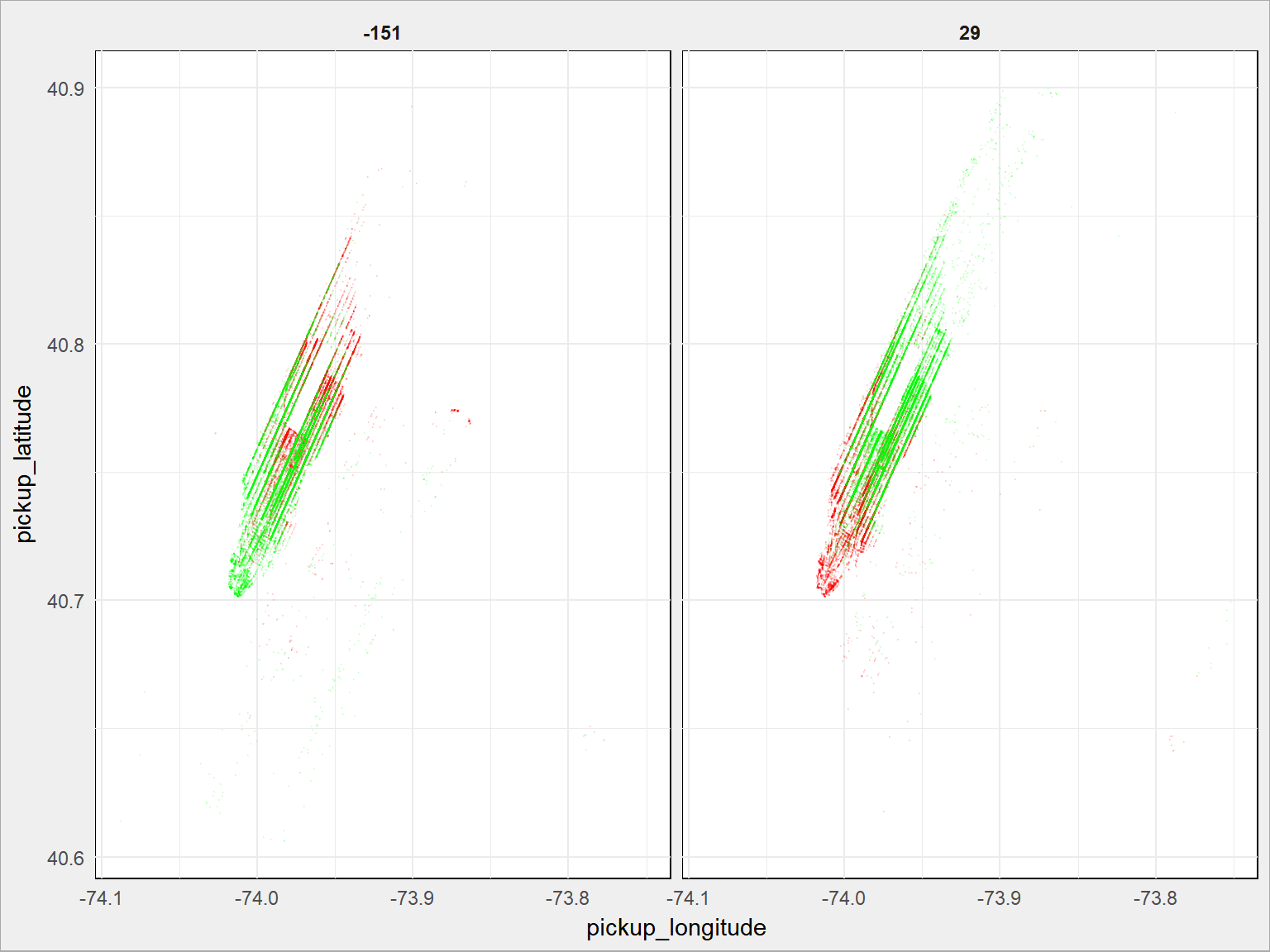
Tam i z powrotem po Manhattanie. Zauważyliście oczywiście, że -151 i 29 to idealnie przeciwne kierunki (suma wartości bezwzględnych to 180). Wystarczyło też użyć przekształcenia układu współrzędnych na wykresie z rozkładem, o tak:
|
1 2 3 4 5 6 7 |
train %>% sample_frac(size = 0.1) %>% mutate(bearing = round(bearing)) %>% count(bearing) %>% ggplot() + geom_bar(aes(bearing, n), stat = "identity") + coord_polar(start = 0) # jedyna dodana linijka! |
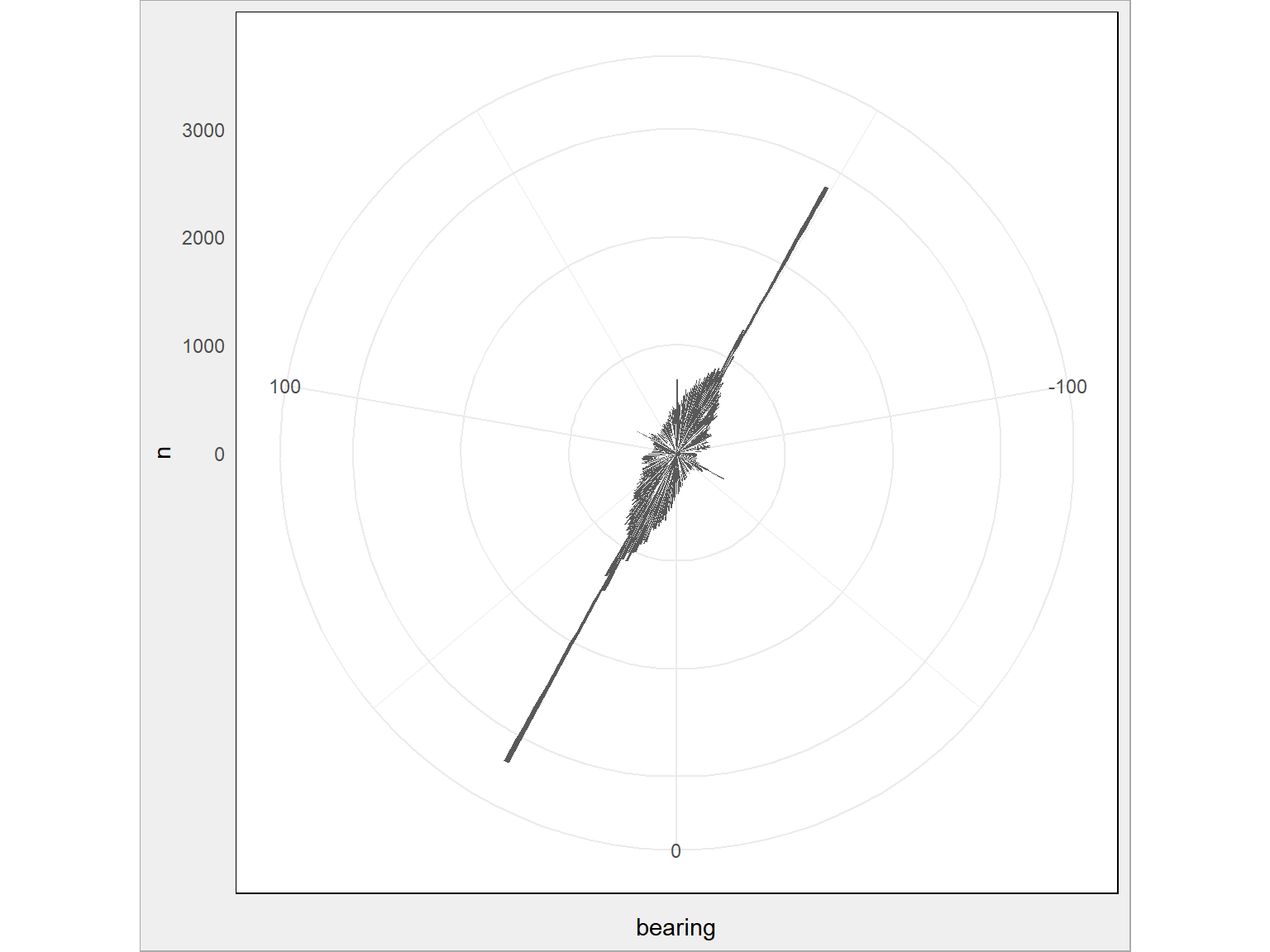
Policzmy teraz wspominaną już prędkość dla każdej z podróży. Odległości mamy w kilometrach, a czas w sekundach – stąd stosowny mnożnik.
|
1 2 3 4 5 6 7 8 |
train <- train %>% mutate(speed = 3600 * trip_distance/trip_duration) train %>% sample_frac(size = 0.1) %>% ggplot() + geom_histogram(aes(speed), binwidth = 1) + scale_y_sqrt() |
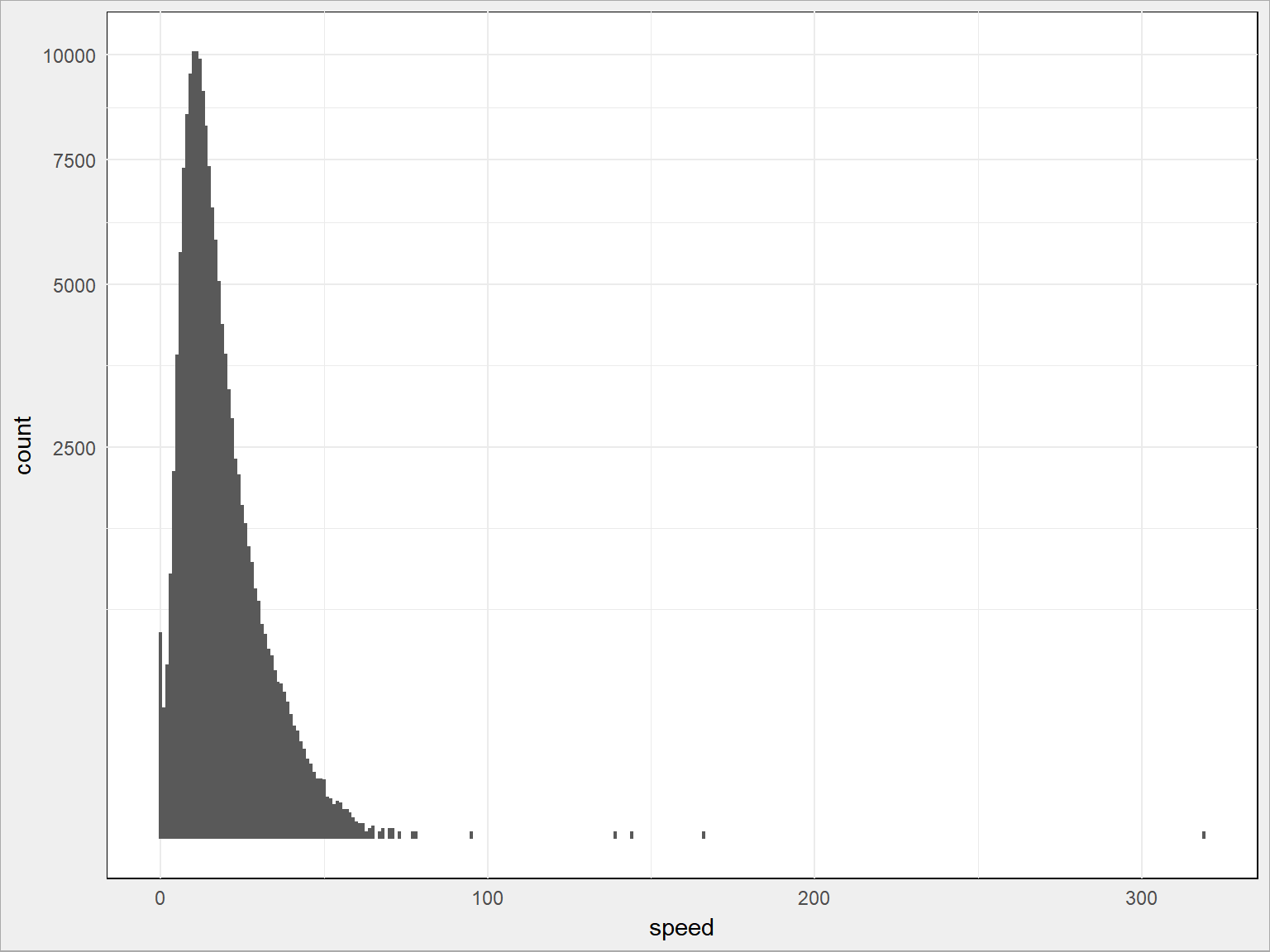
Widać, że bez większej utraty informacji możemy wyciąć te kursy, których prędkość przekracza 90 km/h (można nawet i 75 km/h). Owo 90 wziąłem z przybliżeń, podobnie jak z długością i szerokością geograficzną. Można również obcinać po percentylach albo krotności odchyleń standardowych od średniej (w przypadku rozkładów normalnych).
|
1 |
train <- train %>% filter(speed < 90) |
Możemy teraz przeprowadzić analizę prędkości przejazdu w poszczególnych godzinach lub dniach tygodnia – analogicznie jak robiliśmy to dla ilości przejazdów. Zapewniam, że widać godziny szczytu (i związane z nimi korki). Wystarczy heatmapa:
|
1 2 3 4 5 6 7 8 9 10 |
train %>% group_by(pickup_weekday, pickup_hour) %>% summarise(m_speed = mean(speed)) %>% ungroup() %>% ggplot() + geom_tile(aes(pickup_weekday, pickup_hour, fill = m_speed), color = "white") + scale_fill_gradient(low = "darkred", high = "yellow") + scale_x_continuous(breaks = 1:7) + scale_y_continuous(breaks = seq(0, 24, 3), trans = "reverse") |
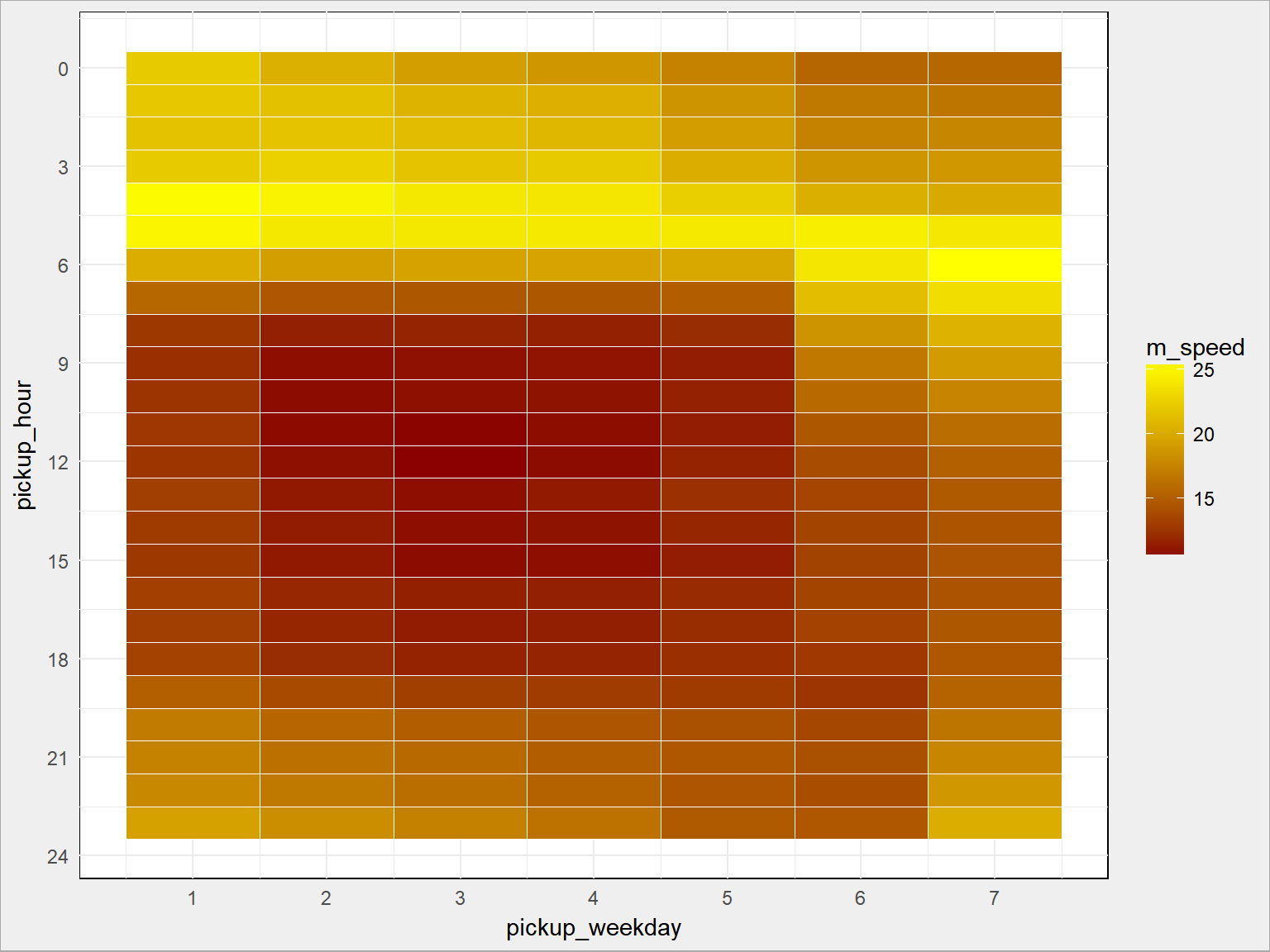
Jak widać jest analogicznie, z tym że odwrotnie (im więcej przejazdów tym mniejsza średnia prędkość).
Lotniska. To ważne miejsca dla taksówek. I już się pojawiły – pamiętacie prawy dolny róg mapki? Pamiętacie kursy długości około 10 i około 20 kilometrów. To właśnie lotniska. W Nowym Jorku są dwa (La Guardia i JFK), z Wikipedii weźmiemy ich współrzędne i oznaczymy odpowiednio punkty rozpoczęcia i zakończenia kursów. Z dokładnością do 2 setnych stopnia, czyli około 2.2 kilometrów. Powinno wystarczyć.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
# La Guardia la_guardia_lon <- -73.872611 la_guardia_lat <- 40.77725 # odjazdy z La Guardia train <- train %>% mutate(lga_pickup = ifelse(pickup_longitude >= la_guardia_lon - 0.02 & pickup_longitude <= la_guardia_lon + 0.02 & pickup_latitude >= la_guardia_lat - 0.02 & pickup_latitude <= la_guardia_lat + 0.02, 1, 0)) # przyjazdy na La Guardia train <- train %>% mutate(lga_dropoff = ifelse(dropoff_longitude >= la_guardia_lon - 0.02 & dropoff_longitude <= la_guardia_lon + 0.02 & dropoff_latitude >= la_guardia_lat - 0.02 & dropoff_latitude <= la_guardia_lat + 0.02, 1, 0)) # JFK airport jfk_lon <- -73.778889 jfk_lat <- 40.639722 # odjazdy z JFK train <- train %>% mutate(jfk_pickup = ifelse(pickup_longitude >= jfk_lon - 0.02 & pickup_longitude <= jfk_lon + 0.02 & pickup_latitude >= jfk_lat - 0.02 & pickup_latitude <= jfk_lat + 0.02, 1, 0)) # przyjazdy na JFK train <- train %>% mutate(jfk_dropoff = ifelse(dropoff_longitude >= jfk_lon - 0.02 & dropoff_longitude <= jfk_lon + 0.02 & dropoff_latitude >= jfk_lat - 0.02 & dropoff_latitude <= jfk_lat + 0.02, 1, 0)) # podróże z lotniska lub na lotnisko? train$jfk_trip <- train$jfk_pickup | train$jfk_dropoff train$lga_trip <- train$lga_pickup | train$lga_dropoff |
Zobaczmy jak dużo wszystkich kursów związanych jest z danym lotniskiem:
|
1 2 3 4 |
train %>% count(jfk_trip, lga_trip) %>% ungroup() %>% mutate(p = round(100*n/sum(n), 1)) |
|
1 2 3 4 5 6 7 |
## # A tibble: 4 x 4 ## jfk_trip lga_trip n p ## <lgl> <lgl> <int> <dbl> ## 1 FALSE FALSE 1353957 93.5 ## 2 FALSE TRUE 53695 3.7 ## 3 TRUE FALSE 39419 2.7 ## 4 TRUE TRUE 742 0.1 |
3.7% kursów to z/na JFK, 2.7% kursów związanych jest z La Guadrią. To odpowiada wysokości słupków na histogramie długości (w sensie odległości) kursów Chcesz to sprawdź, które lotnisko jest przy 10 km, a które przy 20 km. Albo zobacz na mapę ;)
Ciekawostka – 0.1% przejazdów (czyli 742 w pół roku – 4 dziennie, o ile mamy dane o wszystkich kursach) to kursy pomiędzy lotniskami.
Czy czas przejazdu wiąże się z przejazdem do/z lotniska?
Dla lotniska JFK:
|
1 2 3 |
train %>% ggplot() + geom_boxplot(aes(jfk_trip, trip_duration, group = jfk_trip)) |
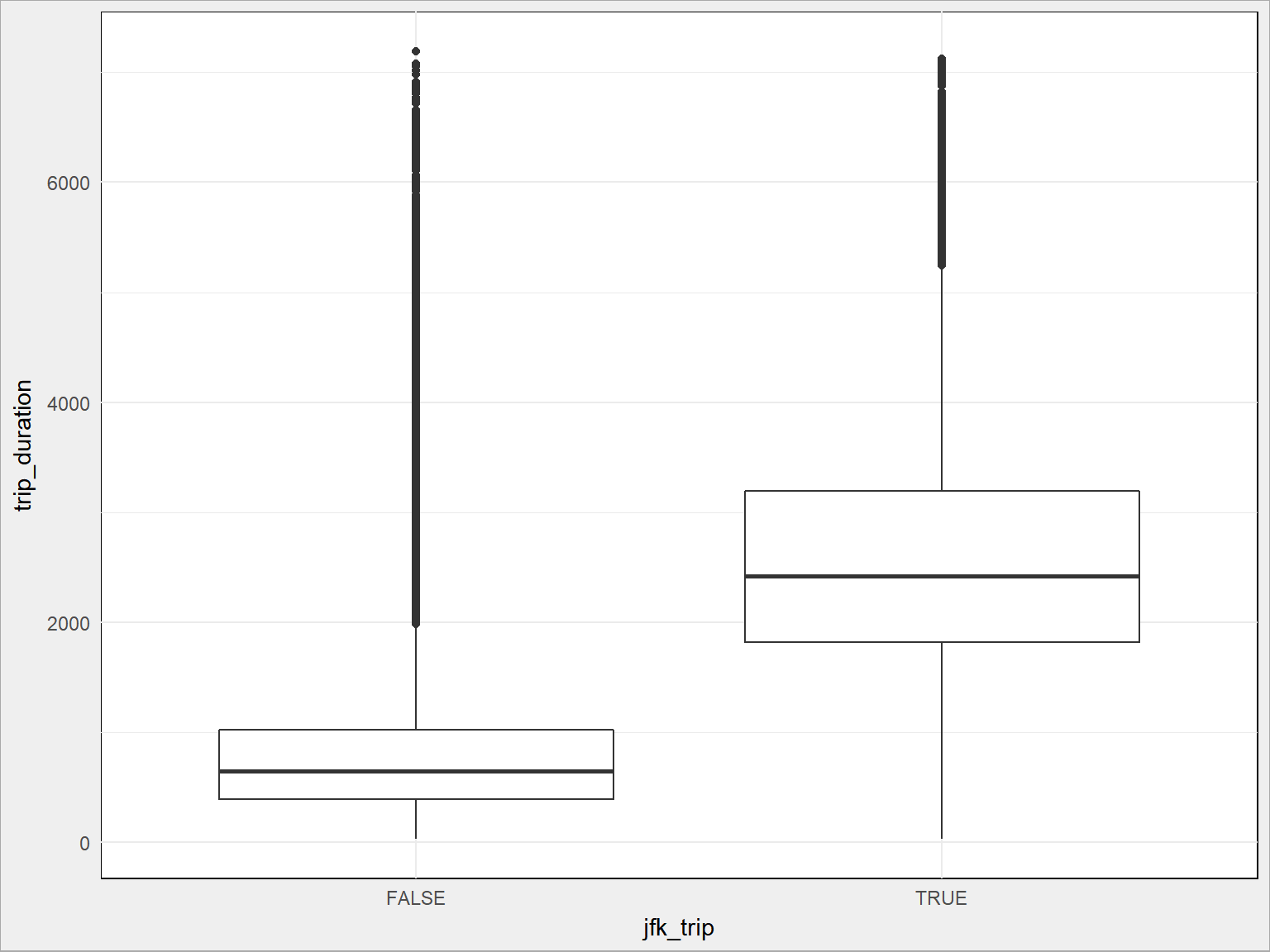
Dla La Guardia:
|
1 2 3 |
train %>% ggplot() + geom_boxplot(aes(lga_trip, trip_duration, group = lga_trip)) |
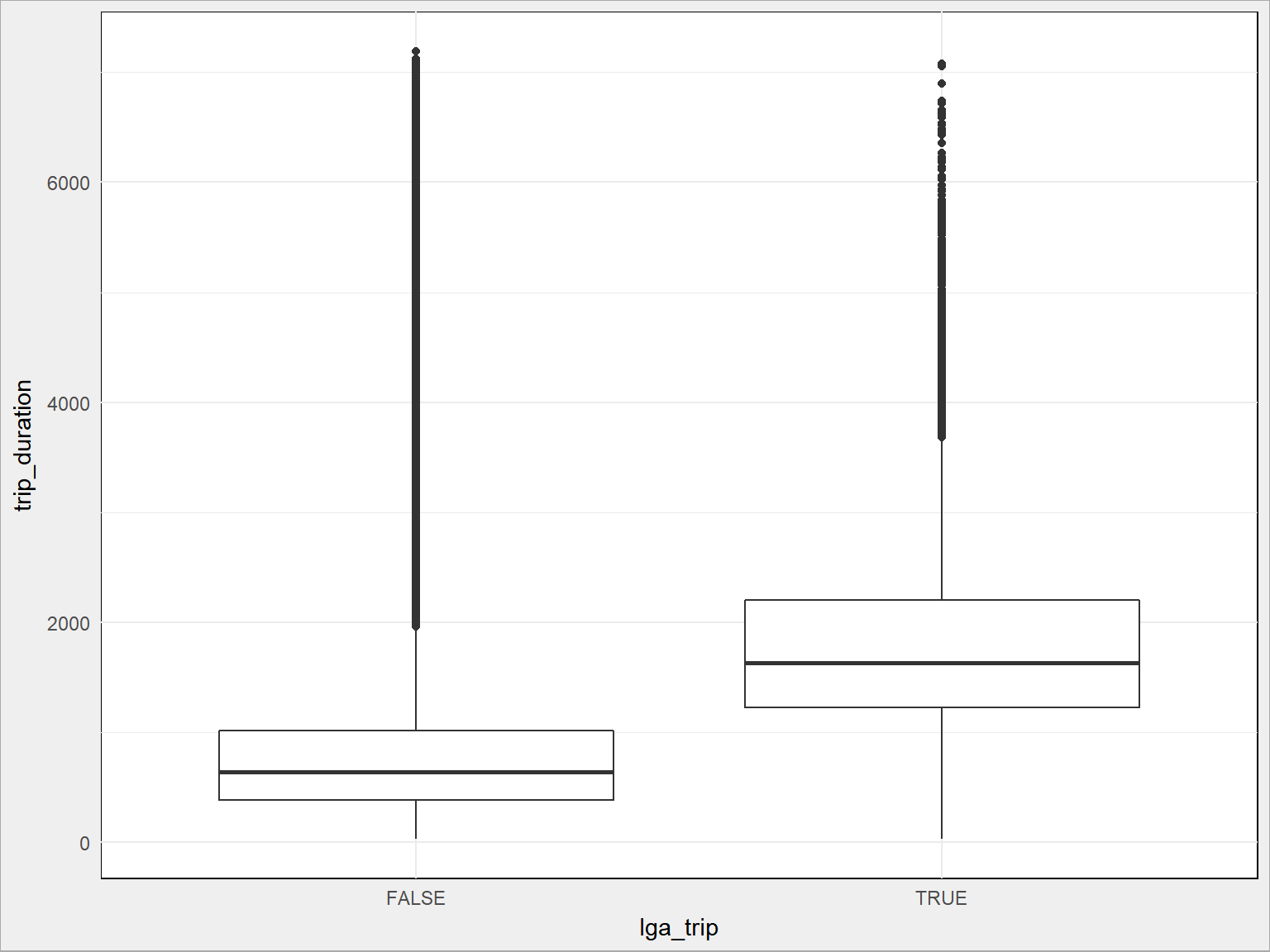
Widać, że kursy do/z lotniskiem mają inną średnią niż cała reszta. To dość oczywiste i już to wiemy ze wcześniejszych wykresów. Większość kursów odbywa się po Manhattanie, lotniska są poza nim w dodaku w różnej odległości. Musi to wpływać na czas przejazdu.
Średni czas podróży w zależności od tego czy kurs dotyczył lotniska (i którego):
|
1 2 3 4 |
train %>% group_by(jfk_trip, lga_trip) %>% summarise(trip_duration = round(mean(trip_duration)/60, 1)) %>% ungroup() |
|
1 2 3 4 5 6 7 |
## # A tibble: 4 x 3 ## jfk_trip lga_trip trip_duration ## <lgl> <lgl> <dbl> ## 1 FALSE FALSE 12.5 ## 2 FALSE TRUE 29.6 ## 3 TRUE FALSE 43.0 ## 4 TRUE TRUE 27.3 |
Znowu mamy dowód, że JFK jest dalej. Czasy chyba podobne do warszawskich (ze Śródmieścia na Okęcie jedzie si ę z 30-45 minut, prawda?).
Teraz spróbujemy czegoś nowego – podzielimy miejsca rozpoczęcia i zakończenia kursów na grupy (klasy). Skorzystamy z algorytmu k-średnich. Przyjmijmy powiedzmy 50 grup. Liczba grup może być istotna dla późniejszego modelu – trzeba eksperymentować.
Jedna uwaga, dość istotna. Tutaj dzielę osobno miejsca rozpoczęcia kursu i jego zakończenia. To oznacza, że:
- grupy mogą nie być identyczne (mogą mieć inny kształt i liczność)
- ten sam punkt może wpaść do grupy A w przypadku rozpoczęcia w nim kursu, a do grupy B w przypadku zakończenia
Wynika to z charakteru algorytmu k-średnich. Poprawnym rozwiązaniem byłoby zebranie wszystkich punktów (pickup i dropoff) do jednej tabeli, a co więcej – razem z tymi samymi współrzędnymi dla danych testowych i podział tej tabeli na grupy. Później (na podstawie współrzędnych) trzeba odpowiednio przepisać dane o przynależności do grupy z powrotem do danych o kursach.
Dla uproszczenia przygotujemy grupy osobno:
|
1 2 3 4 5 6 7 |
# grupy dla rozpoczęcia kursu pickup_cluster <- kmeans(train %>% select(pickup_longitude, pickup_latitude), 50) train$pickup_cluster <- pickup_cluster$cluster # grupy dla zakończenia kursu dropoff_cluster <- kmeans(train %>% select(dropoff_longitude, dropoff_latitude), 50) train$dropoff_cluster <- dropoff_cluster$cluster |
Jak wygląda przypisanie punktów początkowych do grup (czyli: które miejsca miasta są w których grupach)? Zobaczmy na mapie:
|
1 2 3 4 5 6 |
ggmap(ny_map, darken = 0.7) + geom_point(data = train %>% sample_frac(size = 0.1), aes(pickup_longitude, pickup_latitude, color = as.factor(pickup_cluster)), alpha = 0.2, size = 0.1, show.legend = FALSE) + theme(axis.text.x = element_blank(), axis.text.y = element_blank()) + labs(x = "", y = "") |
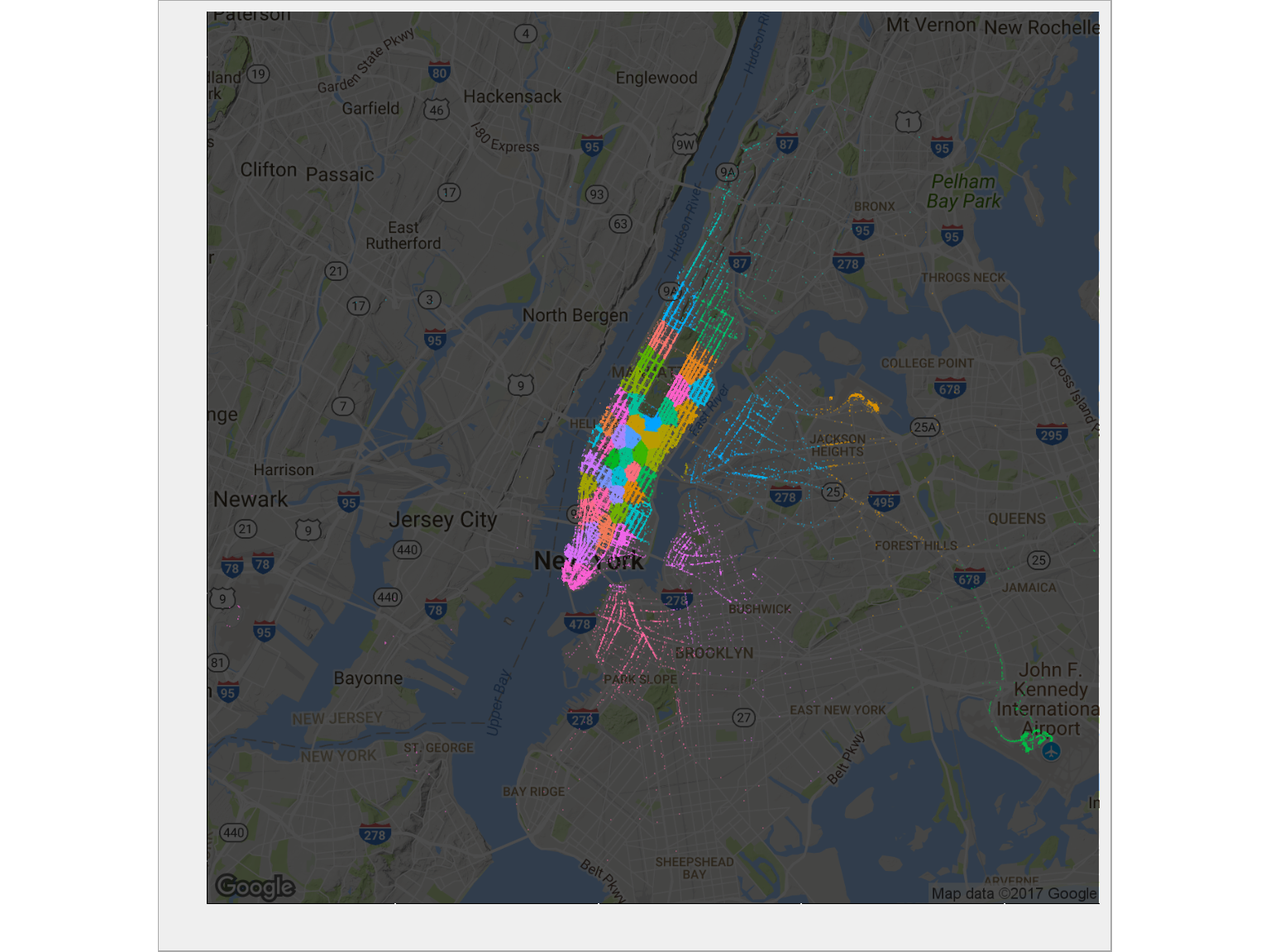
Jest zgodnie z tym czego można było się spodziewać: tam gdzie jest dużo kursów obszary danej grupy są mniejsze. Bardzo ładnie wydzieliło się lotnisko JFK w prawym dolnym rogu, La Guardia wygląda jakby należała do dwóch albo trzech grup? Możemy to sprawdzić:
|
1 2 |
# JFK - pickup train %>% filter(jfk_pickup == TRUE) %>% count(pickup_cluster, jfk_pickup) |
|
1 2 3 4 |
## # A tibble: 1 x 3 ## pickup_cluster jfk_pickup n ## <int> <dbl> <int> ## 1 18 1 29421 |
|
1 2 |
# JFK - dropoff train %>% filter(jfk_dropoff == TRUE) %>% count(dropoff_cluster, jfk_dropoff) |
|
1 2 3 4 |
## # A tibble: 1 x 3 ## dropoff_cluster jfk_dropoff n ## <int> <dbl> <int> ## 1 14 1 11347 |
|
1 2 |
# La Guardia - pickup train %>% filter(lga_pickup == TRUE) %>% count(pickup_cluster, lga_pickup) |
|
1 2 3 4 |
## # A tibble: 1 x 3 ## pickup_cluster lga_pickup n ## <int> <dbl> <int> ## 1 6 1 36543 |
|
1 2 |
# La Guardia - dropoff train %>% filter(lga_dropoff == TRUE) %>% count(dropoff_cluster, lga_dropoff) |
|
1 2 3 4 5 |
## # A tibble: 2 x 3 ## dropoff_cluster lga_dropoff n ## <int> <dbl> <int> ## 1 9 1 4 ## 2 50 1 18680 |
Z danymi o lokalizacji możemy zrobić jeszcze jedną rzecz – przekształcić je za pomocą PCA. Wiele to nie zmieni (z 2D przekształcamy w 2D), ale obrót płaszczyczny i skalowanie współrzędnych może pomóc modelom.
|
1 2 3 4 5 6 7 8 |
train_pickup <- train %>% select(pickup_longitude, pickup_latitude) train_dropoff <- train %>% select(dropoff_longitude, dropoff_latitude) train_pickup_pca <- prcomp(train_pickup, scale. = TRUE) train$pickup_pc1 <- train_pickup_pca$x[,1] train$pickup_pc2 <- train_pickup_pca$x[,2] train_dropoff_pca <- prcomp(train_dropoff, scale. = FALSE) train$dropoff_pc1 <- train_dropoff_pca$x[,1] train$dropoff_pc2 <- train_dropoff_pca$x[,2] |
Jaki to daje wynik? W połączeniu z grupowaniem:
|
1 2 3 4 5 |
train %>% sample_frac(size = 0.1) %>% ggplot() + geom_point(aes(pickup_pc1, pickup_pc2, color = as.factor(pickup_cluster)), alpha = 0.2, size = 0.1, show.legend = FALSE) |
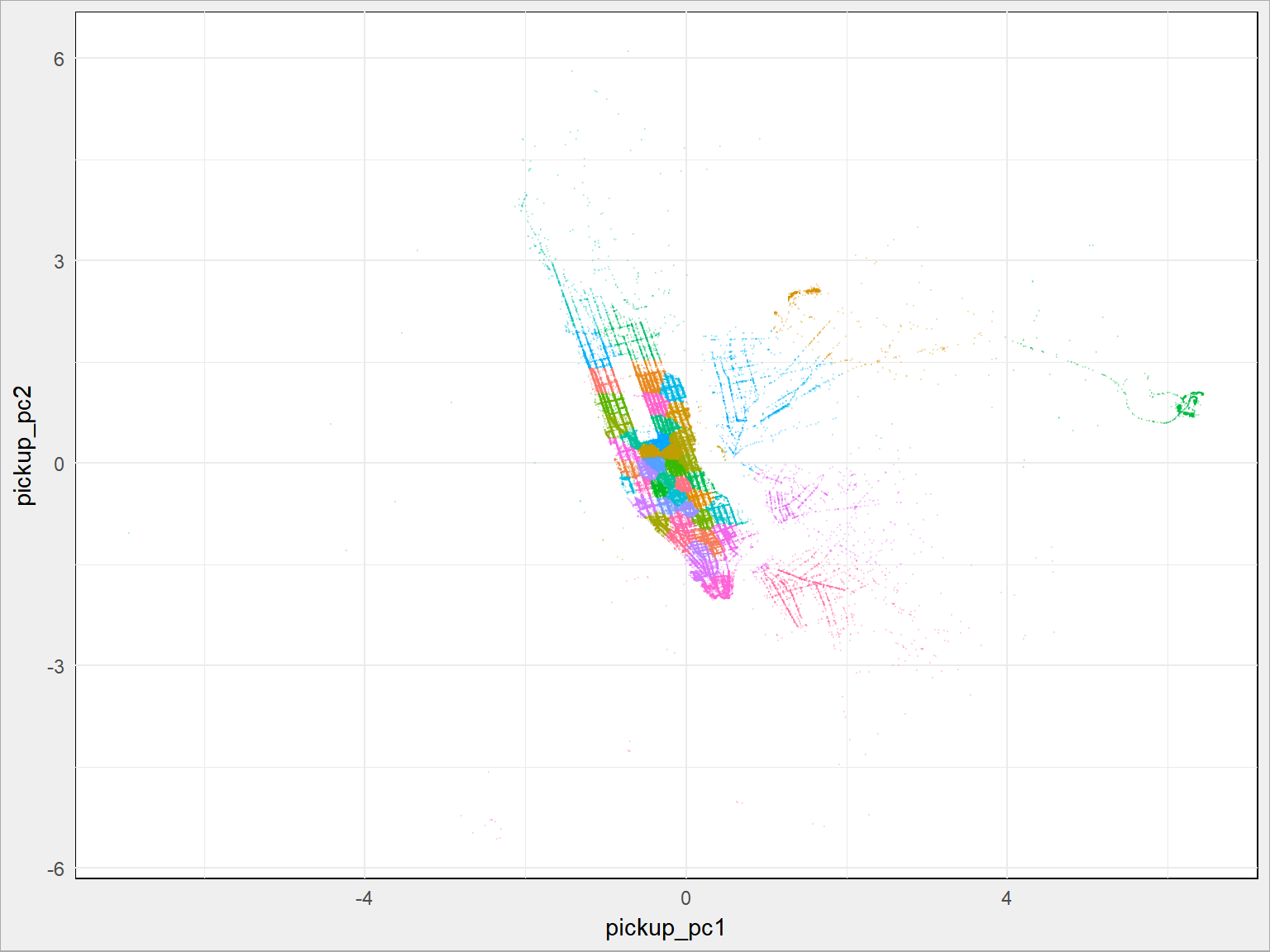
Jak widać całość się obróciła. Nie udało się znaleźć żadnych ukrytych właściwości.
To już wszystkie cechy, które dodaliśmy. Początkowo było ich 11, na koniec mamy 30:
|
1 |
glimpse(train) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
## Observations: 1,447,813 ## Variables: 30 ## $ id <chr> "id2875421", "id2377394", "id3858529", "id3... ## $ vendor_id <int> 2, 1, 2, 2, 2, 2, 1, 2, 1, 2, 2, 2, 2, 2, 2... ## $ pickup_datetime <chr> "2016-03-14T17:24:55Z", "2016-06-12T00:43:3... ## $ dropoff_datetime <chr> "2016-03-14 17:32:30", "2016-06-12 00:54:38... ## $ passenger_count <int> 1, 1, 1, 1, 1, 6, 4, 1, 1, 1, 1, 4, 2, 1, 1... ## $ pickup_longitude <dbl> -73.98215, -73.98042, -73.97903, -74.01004,... ## $ pickup_latitude <dbl> 40.76794, 40.73856, 40.76394, 40.71997, 40.... ## $ dropoff_longitude <dbl> -73.96463, -73.99948, -74.00533, -74.01227,... ## $ dropoff_latitude <dbl> 40.76560, 40.73115, 40.71009, 40.70672, 40.... ## $ store_and_fwd_flag <chr> "N", "N", "N", "N", "N", "N", "N", "N", "N"... ## $ trip_duration <int> 455, 663, 2124, 429, 435, 443, 341, 1551, 2... ## $ pickup_hour <int> 17, 0, 11, 19, 13, 22, 22, 7, 23, 21, 22, 1... ## $ pickup_day <int> 14, 12, 19, 6, 26, 30, 17, 21, 27, 10, 10, ... ## $ pickup_month <int> 3, 6, 1, 4, 3, 1, 6, 5, 5, 3, 5, 5, 2, 6, 5... ## $ pickup_weekday <int> 1, 7, 2, 3, 6, 6, 5, 6, 5, 4, 2, 7, 5, 3, 5... ## $ trip_distance <dbl> 1.5001995, 1.8075298, 6.3922513, 1.4871625,... ## $ bearing <dbl> 99.932546, -117.063997, -159.608029, -172.7... ## $ speed <dbl> 11.869710, 9.814641, 10.834324, 12.479686, ... ## $ lga_pickup <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0... ## $ lga_dropoff <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0... ## $ jfk_pickup <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0... ## $ jfk_dropoff <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0... ## $ jfk_trip <lgl> FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, F... ## $ lga_trip <lgl> FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, F... ## $ pickup_cluster <int> 23, 5, 8, 40, 1, 50, 10, 1, 47, 50, 8, 17, ... ## $ dropoff_cluster <int> 44, 38, 33, 33, 41, 42, 44, 9, 15, 43, 13, ... ## $ pickup_pc1 <dbl> -0.58869976, 0.19431719, -0.42738124, 0.108... ## $ pickup_pc2 <dbl> 0.27167701, -0.44546485, 0.22881807, -1.481... ## $ dropoff_pc1 <dbl> -0.014835579, 0.032648802, 0.048345077, 0.0... ## $ dropoff_pc2 <dbl> 0.0071565805, -0.0049541619, -0.0201723716,... |
Niektóre z cech są silnie skorelowane ze sobą – można je wyeliminować (niewiele wniosą do modelu). Na pewno trzeba zapisać przygotowane dane, żeby nie powtarzać za każdym razem tego samego procesu – jest w końcu dość pracochłonny (liczenie odległości, klasyfikacja punktów do grup). Lepiej czas (komputera, bo przecież mamy już maszynę) poświęcić na przygotowanie modelu.
Ja przejrzałem dla Was dane. Zrobicie dla mnie model?
Wszystkie powyższe operacje należy wykonać również na danych testowych, tak aby modele mogły czerpać z tego samego zestawu cech. Oczywiście nie policzymy prędkości.
Warto sięgnąć również do innych źródeł (konkurs tego nie zabrania) – chociażby godzinowych danych o pogodzie. Czy padał deszcz albo śnieg? Jeśli tak – prędkość spada. Być może pojawią się jakieś ukryte zależności. Jeśli udałoby się uzyskać dane o natężeniu ruchu – też mogą być ciekawe i pomocne. Może warto oznaczyć dni wolne od pracy?
Pominęliśmy całkowicie informacje o liczbie pasażerów i korporacji taksówkowej – warto prześledzić czy te informacje mają wpływ na czas przejazdu. To kilka prostych wykresów, przygotujcie je samodzielnie.
Polecam również zapoznać się z analogicznymi analizami publikowanymi już na Kaggle w ramach konkursów, chociażby bardzo dobrym NYC Taxi Rides EDA. Uzbrojeni w wiedzę o zależnościach pomiędzy zmiennymi i możliwościami wyciągnięcia ukrytych informacji nie musimy poświęcać czasu na samodzielną analizę. Możemy skupić się na przygotowaniu modelu.
Pingback: Newsletter Dane i Analizy, 2024-09-30 | Łukasz Prokulski