Montaż filmowy w Pythonie?

Czy da się automatycznie rozdzielić film na poszczególne ujęcia?

Oczywiście da się. Ale jak do tego podejść?

Dzisiejszy wpis to swego rodzaju zapis sposobu rozwiązania problemu. Wielkiej sztuki programistycznej tutaj nie ma, ale (mam nadzieję) ciekawa jest droga przez całą analizę do uzyskania konkretnego efektu.

Obraz cyfrowy składa się z punktów (określonej ich liczbie – wysokość x szerokość) o różnej barwie. Barwę najczęściej opisują trzy składowe: czerwona, zielona i niebieska (RGB). Wideo to nic innego jak ciąg (kolejne klatki) takich statycznych obrazów.

Weźmy zatem każdą klatkę z filmu i policzmy dla niej jakiś wskaźnik oparty na tym co jest na obrazie. Ten wskaźnik pozwoli nam określić czy dwie sąsiednie klatki różnią się od siebie, z kolei ta różnica da szacunkowe miejsce cięcia pomiędzy ujęciami.

Obraz (kolorowy) składa się z trzech (po jednym dla składowych kolorów: czerwonej, zielonej i niebieskiej) prostokątów wypełnionych wartościami od 0 do 255. Możemy więc dla każdego z tych prostokątów policzyć na przykład średnią wartość, medianę i sumę (suma akurat będzie idealnie związana ze średnią – w końcu średnia to suma podzielona przez liczbę elementów).

Ale przestrzeń barw RGB to nie jedyny sposób na zapis barwy punktu. Możemy ją też zapisać w innych przestrzeniach, na przykład HSV (hue = odcień światła, saturation = jego nasycenie oraz value = moc światła białego). Wykorzystajmy więc również składowe HSV i zbierzmy dla każdej klatki i każdego z kanałów średnią, medianę i sumę wartości składowych.

Do zebrania wszystkich tych informacji użyjemy Pythona i biblioteki OpenCV. Pandas i NumPy przydadzą się też na później:

Pierwsze zadanie to wczytanie klatki z filmu (pliku wideo). W OpenCV jest to wręcz banalne:

W efekcie tych dwóch linii kodu dostaniemy dwie informacje w dwóch zmiennych:

• rst – wynik operacji w postaci True lub False
• frame – obiekt z danymi o kolejnej ramce.

Aby pobrać kolejną ramkę – znowu sięgamy do strumienia przez stream.read(). Co jeszcze ciekawe – jeśli zamiast parametru w postaci ścieżki do pliku wideo podamy zero (czyli stream = cv2.VideoCapture(0)) to naszym wejściowym strumieniem będzie obraz z kamery komputera.

Jak w takiej wczytanej ramce reprezentowany jest obraz? To prosta 3 wymiarowa tablica, a kolejne wymiary to: szerokość, wysokość i liczba składowych koloru. Co ciekawe – na dzień dobry składowe kolorów ułożone są w kolejności BGR czyli odwrotnie niż jesteśmy przyzwyczajeni. I tak tabelka ze składowymi czerwonymi naszej klatki to:

Wyżej wspomniałem o tym, że próbkować każdą klatkę będziemy w przestrzeni barw RGB oraz HSV. Jak zmienić przestrzeń barw? W OpenCV dużo spraw jest prostych, ta w szczególności:

Gotowy skrypt poniżej:

Przydałby się teraz jakiś film, na którym zbadamy wspólnie dalsze pomysły. Nie za długi i z kilkoma rozpoznawalnymi cięciami. Najlepiej kolorowy. Weźmy więc scenę pojedynku z filmu Dobry, zły i brzydki często prezentowaną przy okazji omawiania technik montażu filmowego.

Obejrzyjcie ten krótki fragment, zwróćcie uwagę na to, że ujęcia są bardzo długie, a w kulminacyjnym punkcie cięcia występują coraz częściej. Widać też, że nie wszystkie ujęcia są statyczne – mamy ruch w ramach kadru albo dym z rewolwerów zasłaniający całą klatkę. Spróbuj zapamiętać sekwencję tych elementów.

Film ściągamy z YouTube na przykład przy pomocy narzędzia.

Wróćmy do naszych zabaw pythonowych – możemy przeliczyć całość korzystając z przygotowanego skryptu (zakładam, że nazywa się on skrypt.py). Uruchamiamy więc w konsoli:

Ostatni parametr (T) odpowiada za wyświetlenie w okienku kolejnych klatek filmu. Można oczywiście to sobie odpuścić i wpisać jakąkolwiek inną niż t (duże lub małe) literę. Chwilę to się przemieli (w zależności od długości filmu; podgląd lekko spowalnia całość).

Mając te zaagregowane wartości dla każdej klatki możemy zacząć coś kombinować i szukać sposobu na znalezienie cięć.

Przeanalizujmy w pierwszej kolejności jak kształtują się w czasie poszczególne wartości. Dane zapisałem do pliku good_bad_ugly.csv.

W przestrzeni RGB średnie dla kolejnych klatek wyglądają następująco:

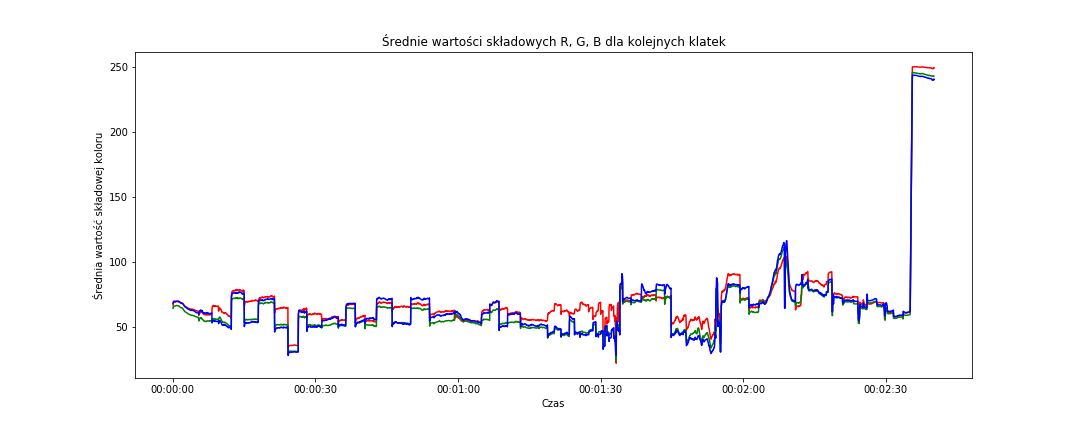
Widzimy przede wszystkim, że pod sam koniec ekran robi się biały. Jeśli zerkniecie w okolice 2:35 to właśnie tak jest – pojawia się plansza z nazwą kanału na YouTube.

Chwilę wcześniej (okolice 2:10) widać wzrost wartości każdej ze składowych w okolice 110 – to koniec właściwego fragmentu filmu i pojawienie się planszy reklamującej inne filmiki, a plansza ta ma sporo szarego. Jednakowe wartości składowych R, G oraz B to odcień szarości (od czarnego z wartościami (0,0,0) do białego – wartości (255,255,255)).

Nas interesuje wszystko to, co dzieje się wcześniej, czyli właściwy fragment filmu Dobry, zły i brzydki. Na poziomie uśrednionych wartości składowych w przestrzeni RGB widać schodki, szczególnie na składowej niebieskiej i zielonej. To, że dzieje się tak akurat dla niebieskiego i zielonego może być szczególnym przypadkiem dla tego filmu. Pamiętajmy, że chcemy przygotować uniwersalny algorytm. Interesują nas zatem gwałtowne różnice pomiędzy kolejnymi ujęciami.

Jedna uwaga – na filmie z YouTube mamy czarne pasy u góry i na dole ekranu, co zaburza pomiary. Dla lepszego efektu dobrze byłoby wyciąć je przed dalszą analizą (OpenCV, a właściwie NumPy, pozwala na to w dość prosty sposób – wystarczy wybrać odpowiedni fragment tablicy crop_img = img[y1:y2, x1:x2]), ale tutaj pominę ten fragment.

Sprawdźmy to samo na medianach:

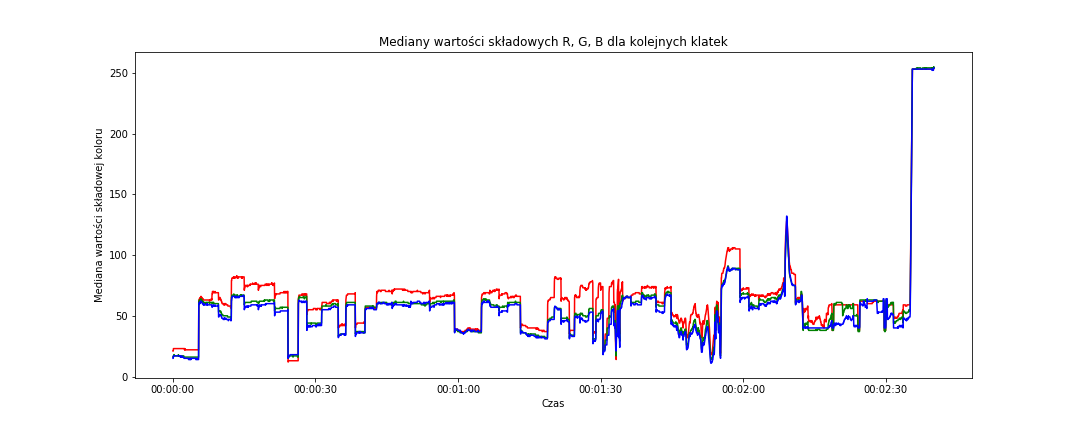
Tutaj jest dość podobnie, szczególnie w końcówce pełnego filmu (czyli z reklamami). Ciekawy jest pik w okolicach 2:10 – jest bardziej spiczasty co dobrze wróży.

Ciekawostką jest natomiast obszar od około 0:45 do 0:55. Na medianach RGB jest dość płasko, na średnich – mamy schody na składowej niebieskiej. Kadr prawie w pełni wypełniają twarze o dość podobnym odcieniu skóry – to jest przyczyną. Oczywiście w połączeniu z właściwością samej mediany.

Sprawdźmy to samo w przestrzeni HSV:

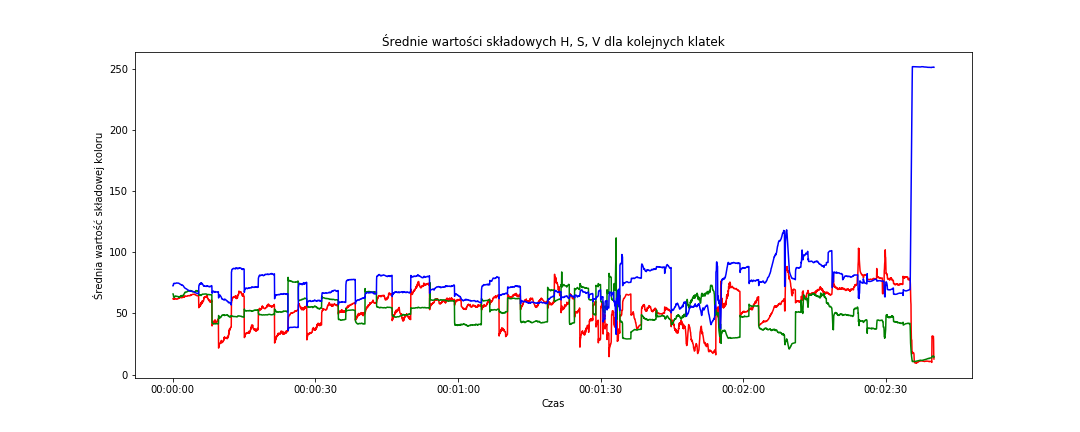
Na poziomie wartości uśrednionych po kanałach (składowych) H, S, V mamy podobny rozkład zębów (albo schodków) jak poprzednio, bardziej rozjeżdżają się składowe. To w sumie nic dziwnego – reprezentują coś innego. Powtarzam – nas interesuje zmiana wartości, a nie sama wartość. Z takiego punktu widzenia schody są podobne jak poprzednio.

Na medianach składowych HSV wygląda to podobnie:

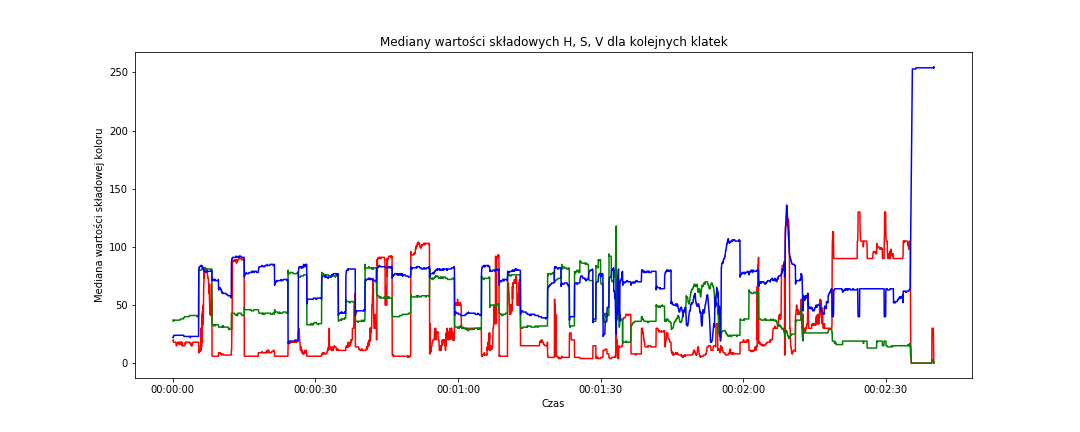
A gdyby uśrednić wszystkie trzy składowe i sprowadzić w ten sposób do jednej liczby dla każdej z klatek? Można będzie wówczas zbadać przebieg tylko tej jednej wartości. Uśrednijmy – zarówno średnie jak i mediany – w ramach obu przestrzeni barw:

I narysujmy to na wykresach:

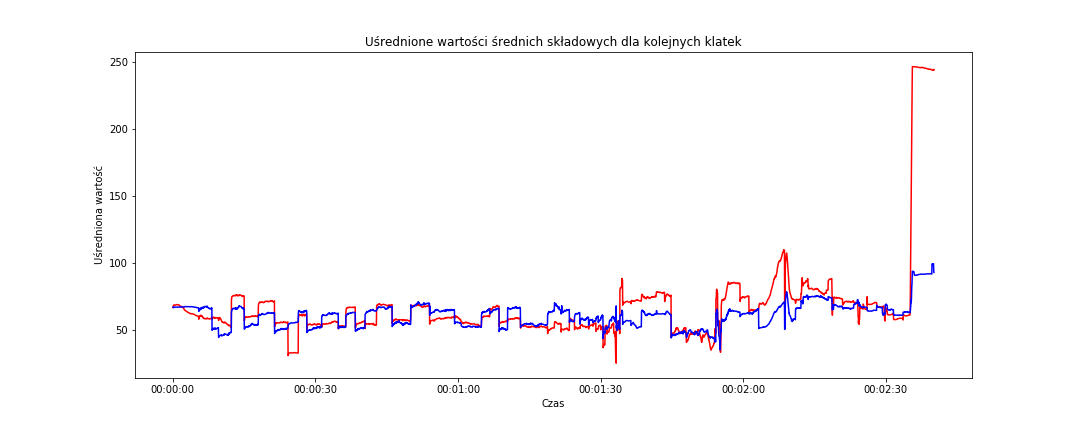
Schodki pojawiają się w podobnych miejscach jak poprzednio (może nieco złagodniały). Większych różnic pomiędzy przestrzeniami barw nie widać (w zasadniczej części filmu – do 2:10). Podobnie jest dla uśrednionych median:

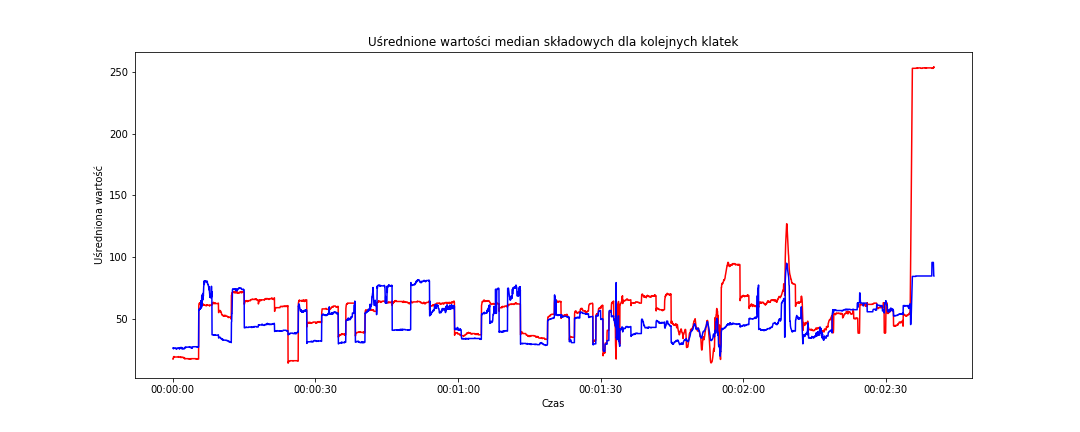
Doprowadziliśmy do tego, że potrafimy zobaczyć skoki poszczególnych parametrów – nieciągłość funkcji. Można zatem pokusić się o znaną z analizy matematycznej pochodną (używaną między innymi do badania zmienności funkcji). A gdyby tak prościej? Na przykład policzyć różnicę (właściwie zmianę procentową) między wartościami dla każdej z kolejnych klatek? O ile procent zmieniła się wartość średniej składowej niebieskiej między klatką dziesiątą a jedenastą? Spróbujmy. Ale już tylko dla uśrednionych wartości średnich i median w każdej z przestrzeni barw.

I narysujmy wykres uśrednionej po składowych zmiany dla średniej i mediany w przestrzeni RGB:

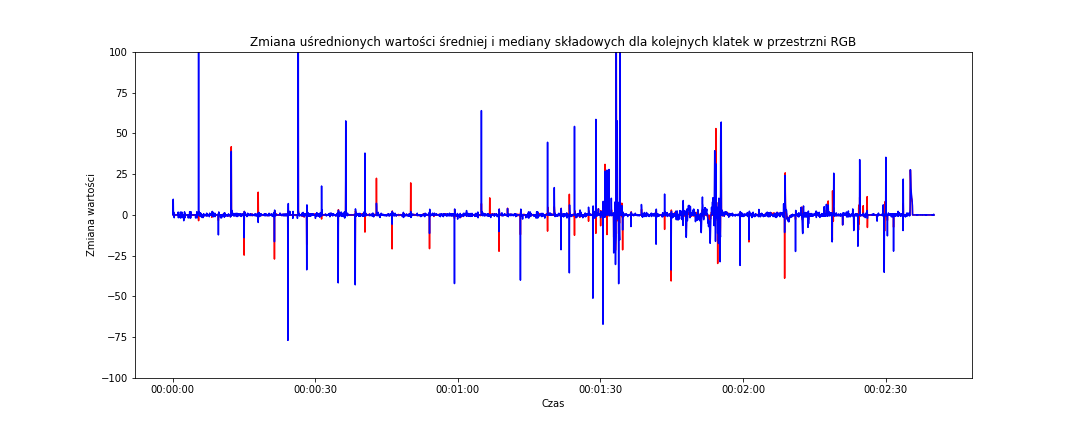
Widzimy, że niebieski kolor (czyli procentowa zmiana wartości uśrednionej mediany składowych kolorów w przestrzeni RGB z kolejnych klatek – zakręcone to, ale jeśli śledzisz tok myślenia od początku to na pewno wiesz o co biega :) na powyższym wykresie jest bardziej zmienny (szpilki zmian są wyższe).

A w przestrzeni HSV?

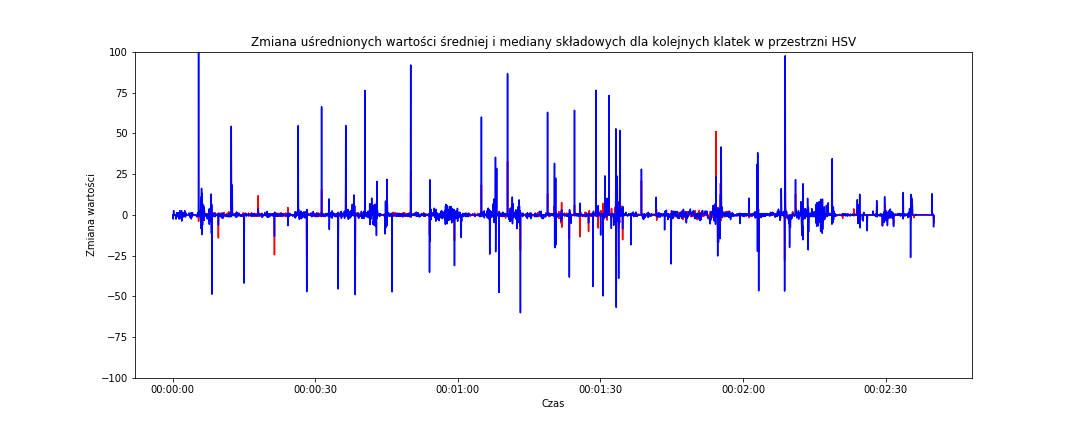
Jest podobnie – znowu niebieski (zatem zmiana mediany) jest bardziej agresywny. Na obu powyższych wykresach zastosowałem tę samą skalę dla osi Y – widać zatem od razu, że szpilki z przestrzeni HSV są wyższe i jest ich więcej. Czy to oznacza, że lepiej oddają cięcia pomiędzy ujęciami? Można tak założyć. Porównajmy jeszcze niebieskie szpilki z obu wykresów (jedna z nich będzie teraz czerwoną linią):

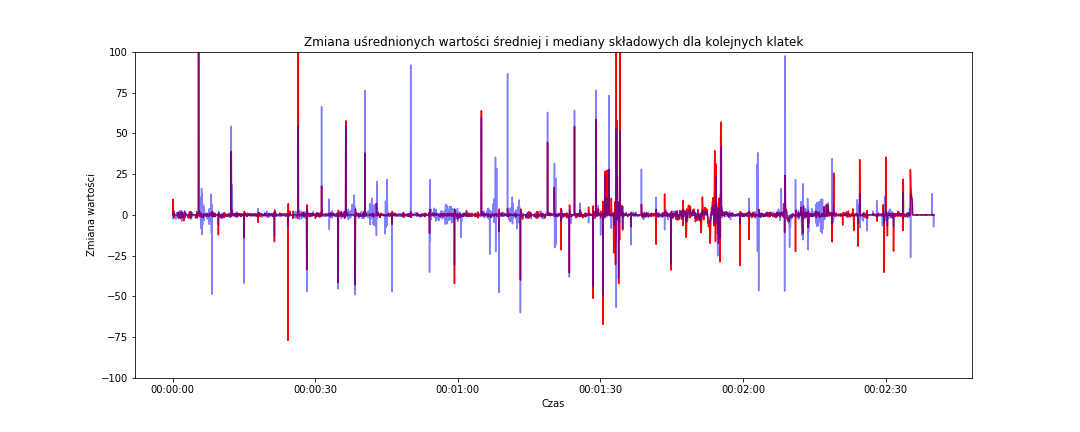
alpha=0.5 dla linii niebieskiej (zmiana mediany HSV) powoduje, że jest ona nieco przeźroczysta i dzięki temu widać gdzie pod nią kończy się czerwona (zmiana mediany RGB). Widać ponownie, że linie odpowiedzialne za przestrzeń HSV są wyższe, bardziej dynamiczne.

Jak wygląda histogram tych różnic?

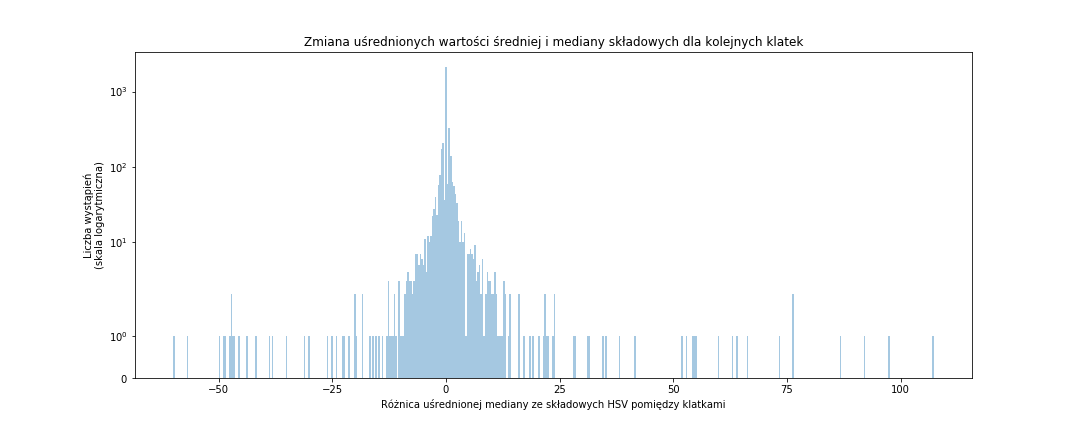
Na podstawie histogramu możemy określić próg zmiany procentowej parametru i tym samym wyznaczyć moment cięcia (jeśli zmiana wartości parametru pomiędzy dwoma klatkami jest ponad tym progiem mamy do czynienia z cięciem montażowym; pod uwagę weźmiemy wartość bezwzględną parametru aby było symetrycznie z obu stron zera). Oczywiście najwięcej będzie małych zmian, nas interesują te odstające wartości.

Zmniejszmy liczbę przedziałów i dodajmy małe niebieskie kreseczki pokazujący każdą z wartości:

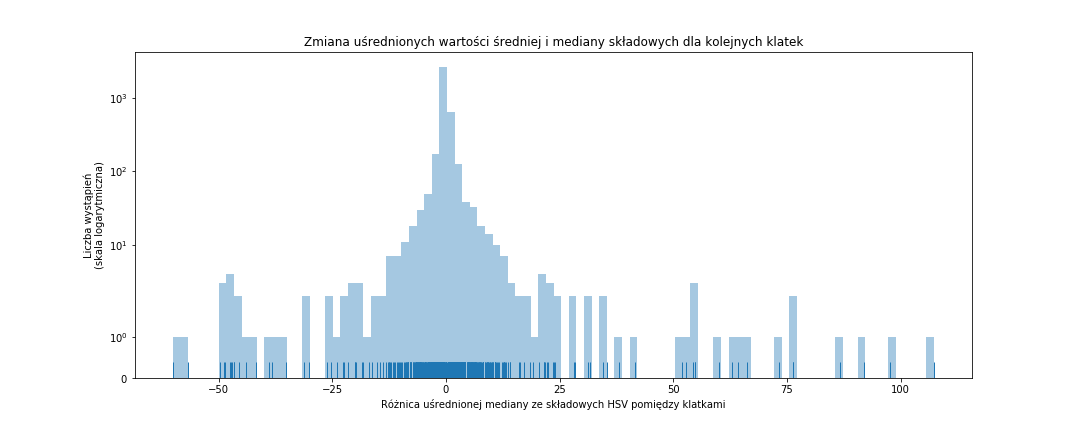
Osobiście wybrałbym próg na poziomie około 15-20%. Dlaczego? Kreseczek jest sporo pomiędzy -20 i 20, ale niemało ich ponad dwuziestką (czy to dodatnią czy ujemną) – może to sugerować, że są z jakiegoś powodu istotne. A przy okazji jest to na tyle duża zmiana, że może rzeczywiście oznaczać zmianę ujęcia. Porównajcie to z wysokością tych niebieskich szpilek gdzieś tam dwa/trzy wykresy wcześniej.

Przygotujmy zatem kolejny skrypt, który przetworzy kolejne klatki, dla każdej z nich obliczy zmianę parametru w stosunku do poprzedniej klatki i jeśli zmiana ta będzie ponad progiem – wyświetli obie sąsiadujące klatki:

Gotowy skrypt możesz uruchomić z konsoli. W wyniku zobaczysz trzy okienka (aktualną klatkę w przestrzni HSV oraz klatki przed i po wykrytym cięciu) oraz informację kiedy miało miejsce cięcie i jaka była różnica naszego wskaźnika.

Mam nadzieję, że spodobał Ci się ten wpis. Nie było tutaj wiele odkrywczych rzeczy, ale też taki postawiłem sobie cel – pokazać proces dochodzenia do algorytmu poprzez analizę otrzymanych danych testowych.

Żeby było śmiesznie – nic w tym odkrywczego. Jest sobie pakiet pySceneDetect który robi to samo na kilka sposobów (a znalazłem go po zakończeniu prac nad własnym podejściem). Wyżej opisany znajdziecie w kodzie w klasie ThresholdDetector.