Zaczynamy cykl związany z sieciami neuronowymi. Zaczniemy od przygotowania danych.
W kilku kolejnych postach posłużymy się danymi z ręcznie pisanymi liczbami. Zbiór ten nazywa się MNIST i jest bardzo popularny w świecie datalogów. Można go pobrać z tego miejsca. Klasyfikacja ręcznie pisanych liczb to takie hello world w sieciach neuronowych.
W kolejnych częściach:
- zbudujemy narzędziownię w R (w oparciu o bibliotekę Keras)
- zbudujemy prostą sieć neuronową i sprawdzimy jakie daje efekty
- zbudujemy sieć konwolucyjną (CNN) i sprawdzimy czy daje lepsze efekty, spróbujemy ją również rozbudować
Pliki jednak nie są w super przyjaznej formie (na przykład w Excelu nie da się ich otworzyć) – na początek więc przetworzymy je na czytelną formę.
Zgodnie z opisem zbiór dzieli się na cztery pliki. Mamy więc dwie (dane treningowe i testowe) paczki: plik określający literki oraz dane opisujące ich wygląd. Pliki są binarne, przetworzymy je na pliki CSV.
|
1 2 |
library(tidyverse) library(gridExtra) |
Ściągamy pliki .GZ i rozpakowujemy je. W dalszej części wpisu zajmiemy się tylko plikiem z danymi treningowymi. Sama konwersja danych testowych jest identyczna.
|
1 2 3 4 5 |
train_labels_path <- "data/train-labels.idx1-ubyte" train_images_path <- "data/train-images.idx3-ubyte" train_labels <- read_file_raw(train_labels_path) train_images <- read_file_raw(train_images_path) |
Pierwszy krok to labelki, czyli jaką liczbę pokazują dane? To prosta sprawa – wystarczy poszczególne bajty zamienić na wartości liczbowe:
|
1 |
labels <- train_labels[9:length(train_labels)] %>% as.numeric() |
I już! Kolejne elementy tablicy to po prostu liczby mówiące nam co widzimy na obrazku.
Obrazki są nieco trudniejsze w obsłudze. Każda liczba zapisana jest w postaci obrazka 28 na 28 pikseli. Początek pliku to jakieś dane informacyjne (opisane na stronie ze zbiorem), a później mamy 60 tysięcy ciągów 784 bajtów (28*28) opisujących wygląd pisanych liczb (60 tysięcy).
Wybieramy zatem po te 784 bajtów, układamy je w wiersz, na początku wiersza dodajemy odpowiedni label i całość upychamy w wielką tablicę:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
train_all <- tibble() for(n_pic in 0:length(labels)) { pixels <- train_images[(17+n_pic*28*28):(17+(n_pic+1)*28*28-1)] %>% as.numeric() data_row <- c(labels[n_pic+1], pixels) train_mat <- matrix(data_row, nrow = 1) %>% as_tibble() colnames(train_mat) <- c("label", paste0("pixel", 0:783)) train_all <- bind_rows(train_all, train_mat) } |
Proces jest pracochłonny, dlatego od razu zapisujemy wynik do pliku CSV:
|
1 |
write_csv(train_all, path = "data/train_converted.csv", col_names = TRUE) |
Podobne zabiegi trzeba dokonać dla danych testowych (odpowiednio modyfikując ścieżkę do plików i przesunięcie – w danych testowych opisujących obraz nie ma kilku bajtów).
Zobaczmy ile jest liczb w danych treningowych?
|
1 2 3 4 5 |
train_all %>% count(label) %>% ggplot() + geom_col(aes(label, n), fill = "lightgreen", color = "grey50") + scale_x_continuous(breaks = 0:9) |
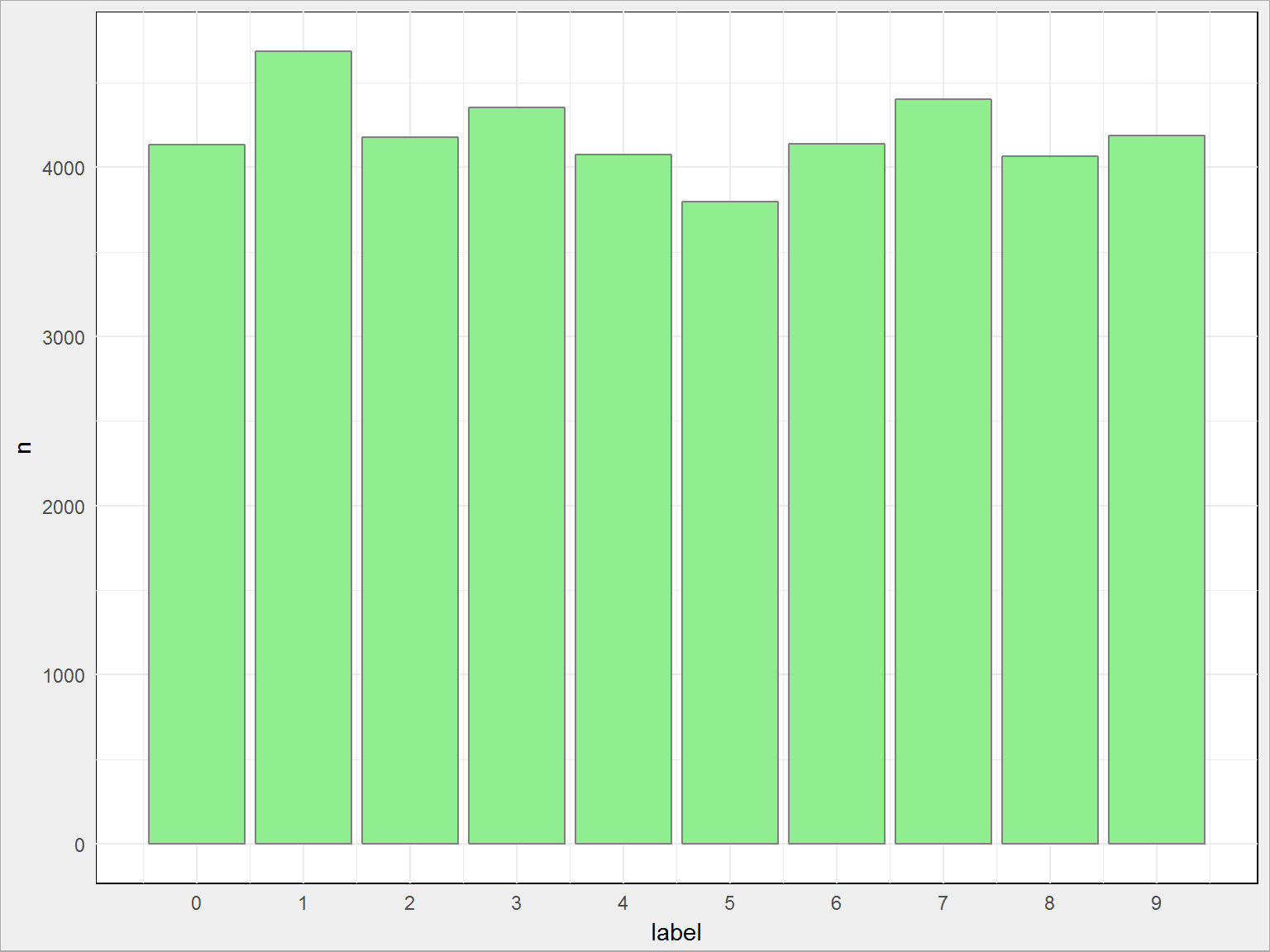
Rozkład jest mniej więcej równomierny.
Na razie mamy do czynienia z danymi w postaci cyferek, ale czy możemy je pokazać? Napiszemy funkcję, która z całych danych treningowych wybierze jeden wiersz i jego zawartość pokaże w formie graficznej.
Jedyne co trzeba zrobić to ciąg 784 liczb (o wartości od 0 do 255 co odpowiada stopniowi zaczernienia punktu) złożyć w macierz 28×28 punktów i ją pokazać. Dodatkowo, aby obraz nie był odbity w pionie (punkt 0,0 jest w lewym dolnym rogu dla wykresów, ale dla obrazków jest to lewy górny róg) musimy go obrócić.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
showDigit <- function(dataset=train_all, digit_number=1) { # wybieramy wskazany wiersz i składamy w macierz 28x28 punktów matrix1 <- dataset[digit_number, 2:dim(dataset)[2]] %>% as.numeric() %>% matrix(ncol = 28, byrow = T) # miejsce na odwróconą macierz matrix2 <- matrix(rep(0, 28*28), 28, 28) # odwrócenie osi Y (punkt 0,0 na górze, a nie na dole) for(i in 1:28) for(j in 1:28) matrix2[28-i, j] <- matrix1[i, j] # pokazujemy obrazek, w dodatku macierz musimy transponować (zamienić wiersze na kolumny) image(t(matrix2), col = rev(topo.colors(255)), axes = FALSE) # dodajemy tytuł, który powie nam co za liczbę oglądamy :) title(dataset[digit_number,1] %>% as.numeric()) } |
Zamiast podwójnego fora można użyć kombinacji apply() z rev() .
Pokażmy jakąś losową liczbę:
|
1 |
showDigit(train_all, sample(nrow(train_all), 1)) |
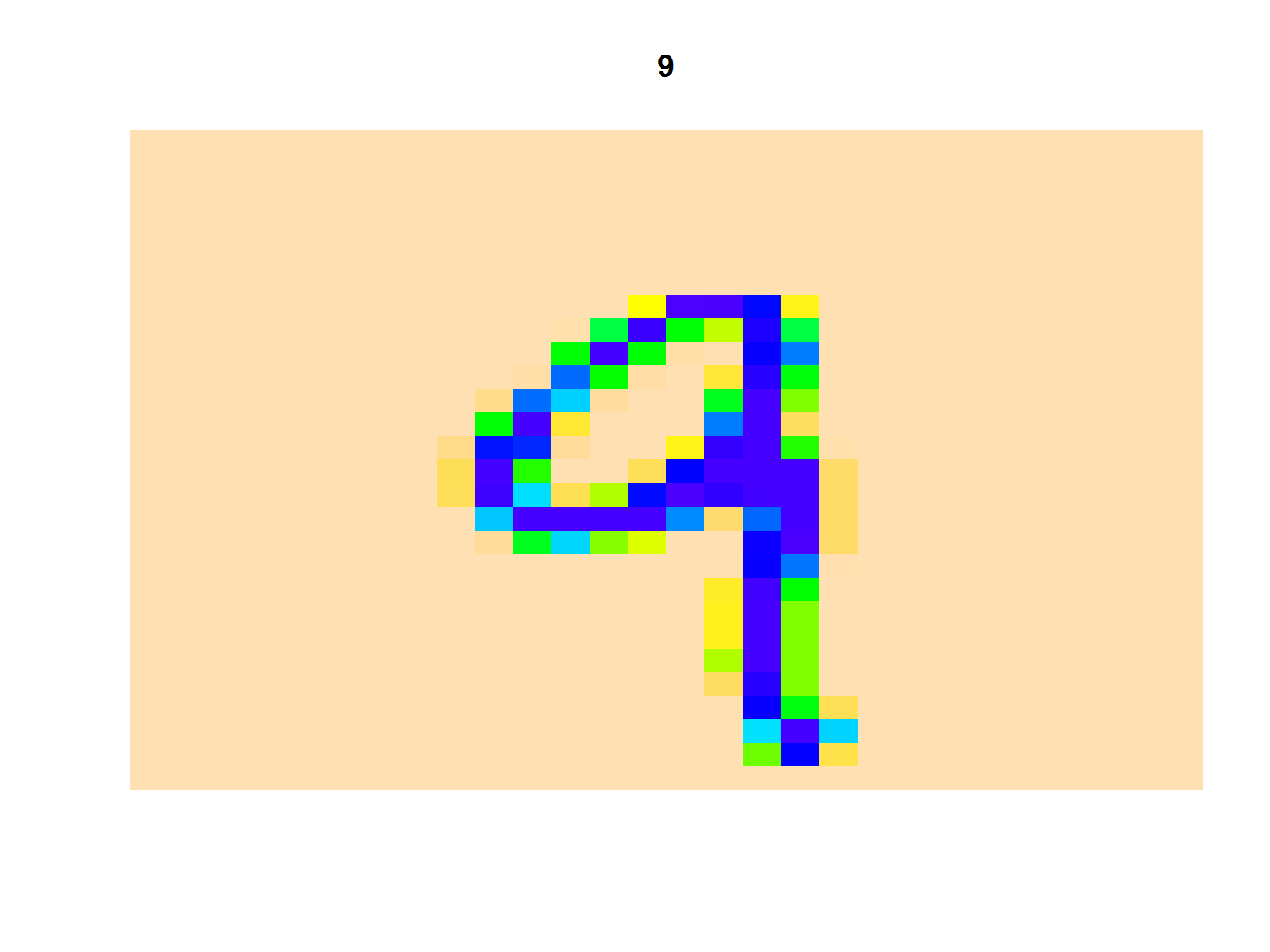
Działa.
Teraz zróbmy coś podobnego, ale z pomocą ggplot. I żeby nie było tak samo – weźmiemy 12 losowo wybranych szóstek:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
# miejsce na kolejne obrazki szóstek plots <- list() # wybieramy 12 szóstek for(i in 1:12) { # weź losowy wiersz z danych, ale opisujący szóstkę digits_data <- train_all[train_all$label == 6, ] %>% sample_n(1) # do listy wykresów dodajemy to co uzyskamy: plots[[i]] <- digits_data %>% # dane z szerokich przekształcamy na długie gather() %>% # usuwamy informację o labelce - zostanie nam 784 wierszy filter(key != "label") %>% # numerujemy je kolejno mutate(row = row_number()-1) %>% # zapisujemy numer kolumny i wiersza - czyli części: # całkowitą dzielenia numeru punktu przez 28 i resztę z tego dzielenia mutate(col = row %% 28, row = row %/% 28) %>% # rysujemy całość ggplot() + geom_tile(aes(col, 28-row, fill=value), show.legend = FALSE) + scale_fill_gradient(low = "white", high = "black") + coord_equal() + theme_void() + theme(plot.background = element_rect(fill = "gray80")) } # wszystkie wygenerowane obrazy układamy na jednym obrazku do.call("grid.arrange", c(plots, ncol = 4, nrow = 3)) |

Jak widać szóstki są różne, proces kategoryzacji danych testowych będzie zatem dość trudny. Ale to w kolejnej części.
Spróbujmy zobaczyć uśrednione wartości dla każdej z liczb. Wykorzystamy w znacznym stopniu powyższy kod. Zamiast rysować pojedyncze szóstki – przygotujemy 10 wierszy (liczby od 0 do 9) z uśrednionymi danymi:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
plots <- list() for(i in 0:9) { # uśredniamy dane dla kolejnych liczb digits_data <- train_all[train_all$label == i, ] %>% map_df(mean) # analogicznie jak dla szóstek je rysujemy plots[[i+1]] <- digits_data %>% gather() %>% filter(key != "label") %>% mutate(row = row_number()-1) %>% mutate(col = row %% 28, row = row %/% 28) %>% ggplot() + geom_tile(aes(col, 28-row, fill=value), show.legend = FALSE) + scale_fill_gradient(low = "white", high = "black") + coord_equal() + theme_void() + theme(plot.title = element_text(hjust = 0.5, size = 15), plot.background = element_rect(fill = "gray80")) plots[[i+1]] <- plots[[i+1]] + labs(title = paste("Liczba ", i)) } # pokazujemy całość do.call("grid.arrange", c(plots, ncol = 5, nrow = 2)) |
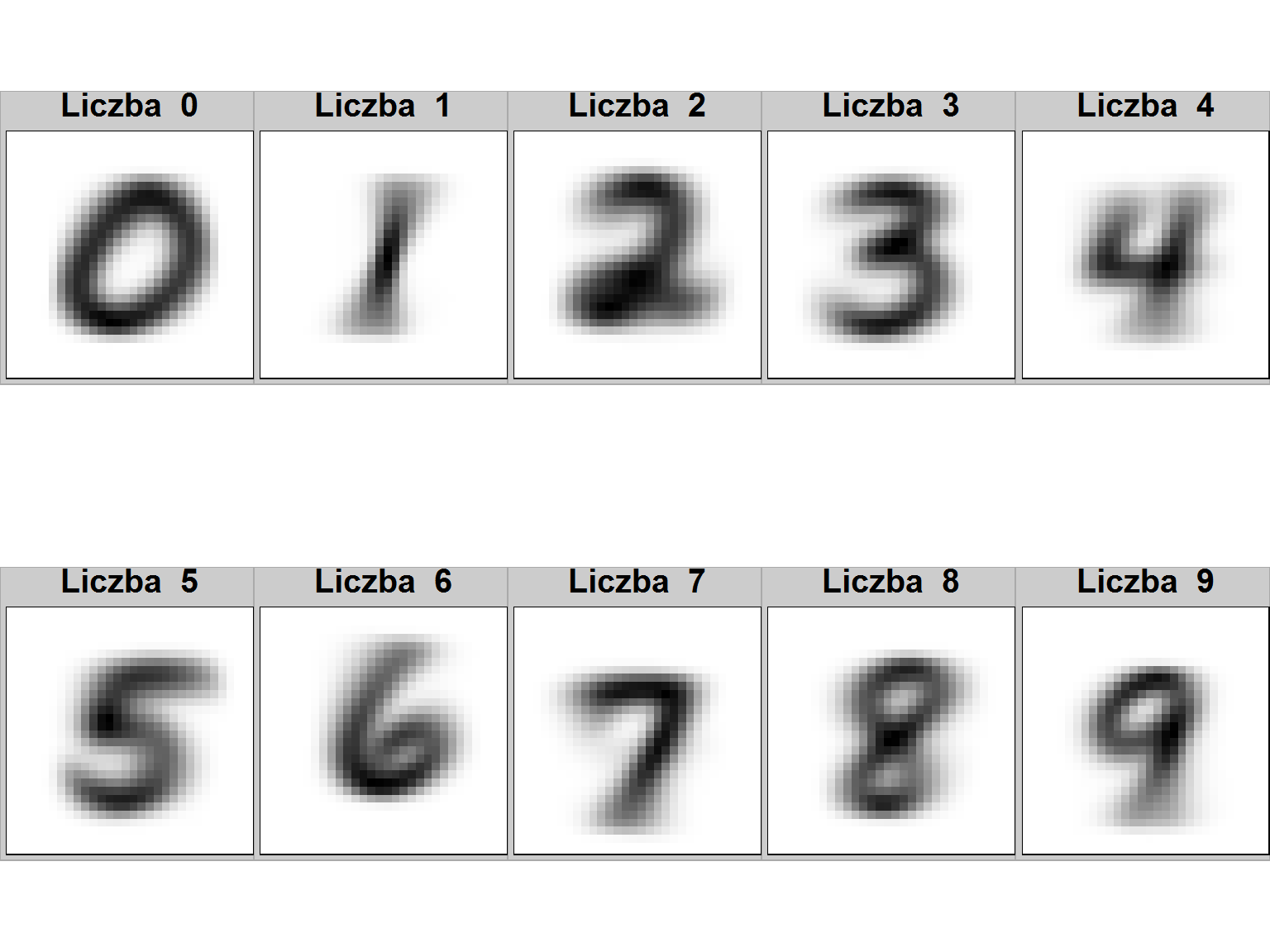
Widać, że niektóre z liczb są w miarę “zwarte”, w pewnym sensie można wyróżnić miejsca, przez które musi przechodzić linia w każdym z wariantów zapisu danej liczby. To cenna obserwacja, zapamiętajcie ją.
A na koniec niespodzianka: zamiast przygotowywać dane w CSV z oryginalnego zbioru MNIST można je po prostu ściągnąć z Kaggle.com. Dalsze części opierać się będą właśnie na danych z Kaggle.
Bardzo ciekawie się zaczyna, czekam na kolejne wpisy :)
co by sie stało gdybyś wyliczyl lepszą dokładność niż inni?
Musiałbym napisać jakiś poważny artykuł naukowy pewnie… Poza tym kariera, kobiety, wino, śpiew, wizyty w zakładach pracy… ;)