Jakie wina sprzedają się najlepiej? Czy Polacy lubią wino czerwone czy białe? Słodkie czy wytrawne? Jak wybrać wino dobre i tanie?
Dane na potrzeby analizy pobierzemy ze sklepu internetowego. Odpowiedni skrypt (i pobrane dane) znajdziecie w repo na GitHubie, w pliku get_data.R. Skrypt jest dość długi, nie wnosi niczego ciekawego do samej analizy.
Po zebraniu danych możemy przystąpić do EDA (eksploracji danych). Potrzebujemy właściwie tylko pakietu tidyverse (od zaktualizowanej kilka dni temu wersji w skład ekosystemu wchodzą stringr i forcats; w przyszłości przydałoby się jeszcze lubridate dla kompletu).
Wczytujemy więc zapisane dane, lekko je modyfikujemy (ze względu na późniejszą kolejność i porządek na wykresach).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
library(tidyverse) library(forcats) # zbędne dla tidyverse >= 1.2.1 library(stringr) # zbędne dla tidyverse >= 1.2.1 # wczytujemy zapisane dane lista_win <- readRDS("lista_win.RDS") # trochę poprawek lista_win$popularnosc <- as.numeric(lista_win$popularnosc) lista_win$expert_rating_ocena <- factor(lista_win$expert_rating_ocena, levels = c("wina poprawne", "wina dobre", "wina bardzo dobre", "wina wyjątkowe", "idealne")) lista_win$smak <- factor(lista_win$smak, levels = c("Półsłodkie", "Słodkie", "Półwytrawne", "Wytrawne")) lista_win$kolor <- factor(lista_win$kolor, levels = c("Białe", "Czerwone", "Różowe", "Inne")) lista_win$region <- ifelse(lista_win$region == "WOJEWÓDZTWO ZACHODNIOPOMORSKIE", "Zachodniopomorskie", lista_win$region) lista_win$region <- ifelse(lista_win$region == "WOJEWÓDZTWO LUBUSKIE", "Lubuskie", lista_win$region) |
W pierwszej kolejności zrobimy remanent: zobaczymy co oferuje sklep. Jakie wina ze względu na pochodzenie, smak czy kolor.
|
1 2 3 4 5 6 7 |
lista_win %>% count(kraj) %>% arrange(n) %>% mutate(kraj = factor(kraj, levels = kraj)) %>% ggplot() + geom_col(aes(kraj, n), color = "gray50", fill = "#a6d96a") + coord_flip() |
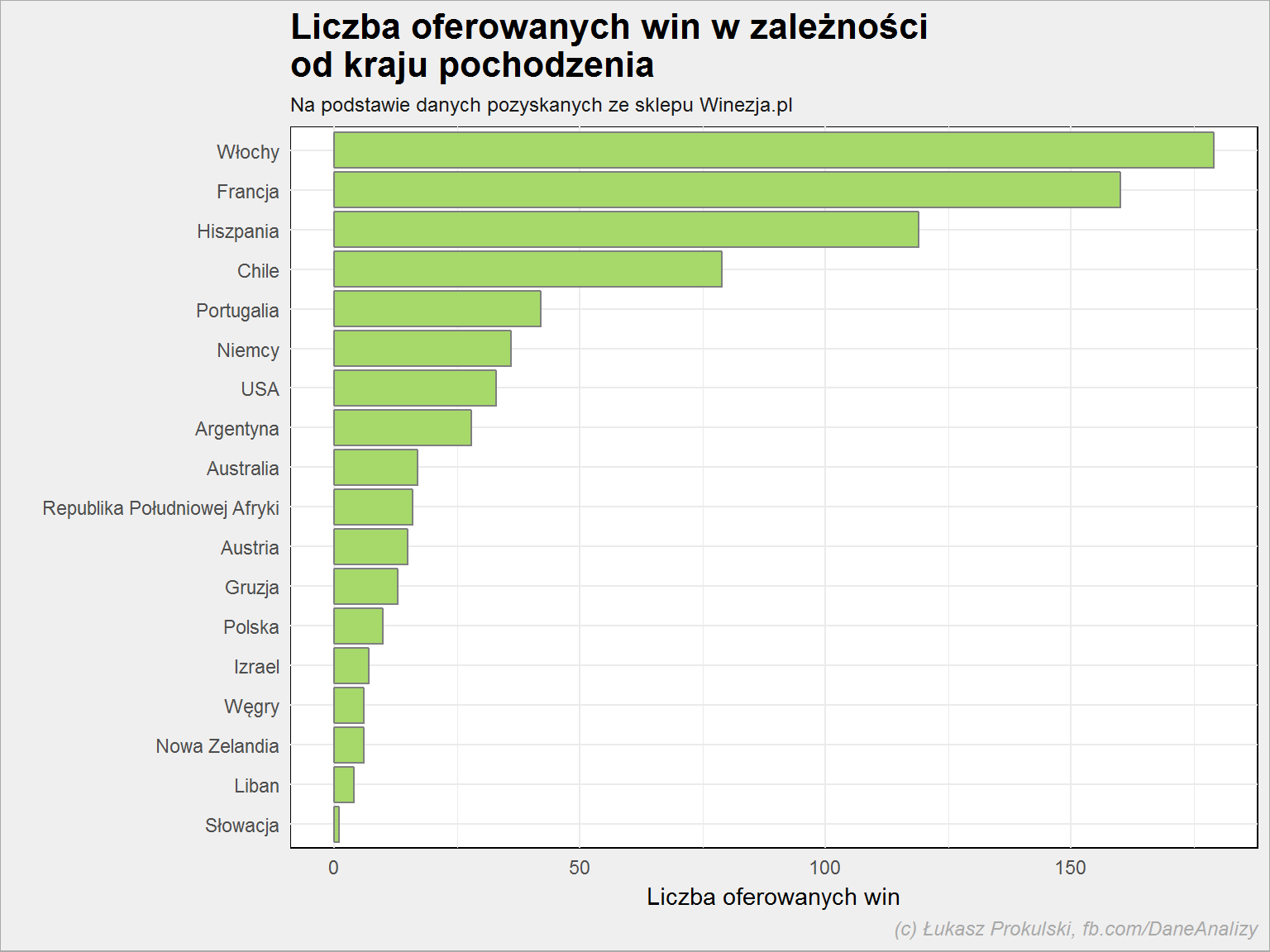
Najwięcej oferowanych win pochodzi z Włoch i Francji, kolejna jest Hiszpania i Chile. Nie ma w tym nic dziwnego. Z jednej strony kraje te “od zawsze” produkują wina, a drugiej – te wina są najpopularniejsze.
|
1 2 3 4 5 6 7 8 9 10 |
lista_win %>% count(smak) %>% filter(!is.na(smak)) %>% arrange(n) %>% mutate(smak = factor(smak, levels = smak)) %>% mutate(p = 100*n/sum(n)) %>% ggplot() + geom_col(aes(smak, n), color = "gray50", fill = "#a6d96a") + geom_text(aes(smak, n, label = sprintf("%.1f%%", p)), hjust = 1.1) + coord_flip() |

Najwięcej oferowanych jest win wytrawnych. Niektórzy twierdzą, że inne smaki to nie wino ;)
|
1 2 3 4 5 6 7 8 |
lista_win %>% count(kolor) %>% filter(!is.na(kolor)) %>% arrange(n) %>% mutate(kolor = factor(kolor, levels = kolor)) %>% ggplot() + geom_col(aes(kolor, n), color = "gray50", fill = "#a6d96a") + coord_flip() |
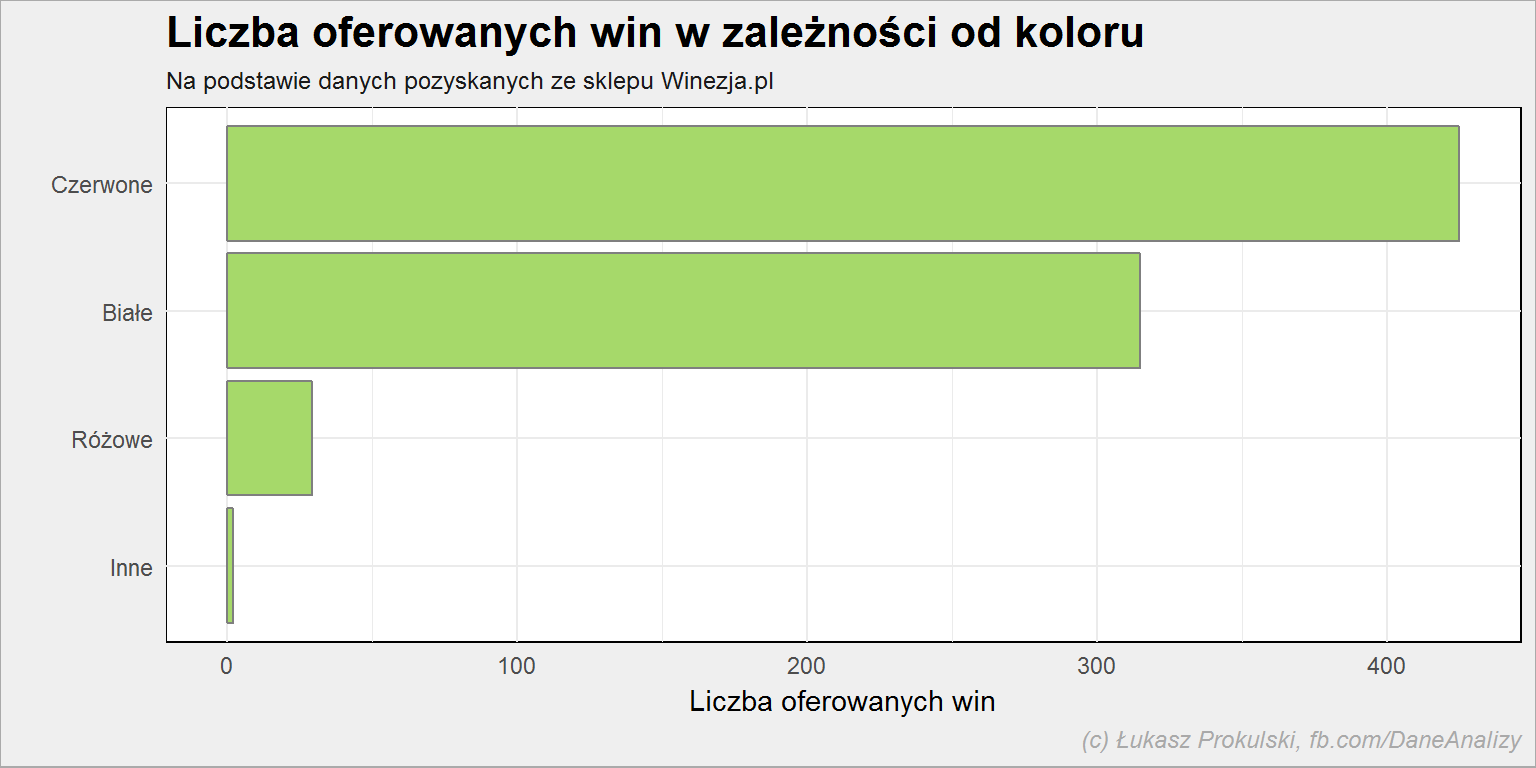
Jeśli zaś chodzi o kolor to oczywiście dominuje czerwony (55% oferowanych win). Niemalże 41% to wina białe. Kolor “inny” mają dwa wina (andaluzyjskie “Alma Azul Blue Chardonnay” w wersji spokojnej i musującej).
Zobaczmy jeszcze jak wygląda przekrój smaku i koloru – więcej jest wytrawnych białych czy czerwonych?
|
1 2 3 4 5 6 7 8 9 10 |
lista_win %>% filter(!is.na(smak)) %>% count(kolor, smak) %>% ungroup() %>% mutate(p = 100*n/sum(n)) %>% ggplot() + geom_tile(aes(kolor, smak, fill = n), color = "gray50") + geom_text(aes(kolor, smak, label = sprintf("%d\n(%.1f%%)", n, p))) + scale_fill_distiller(palette = "YlOrBr") + theme(legend.position = "bottom") |
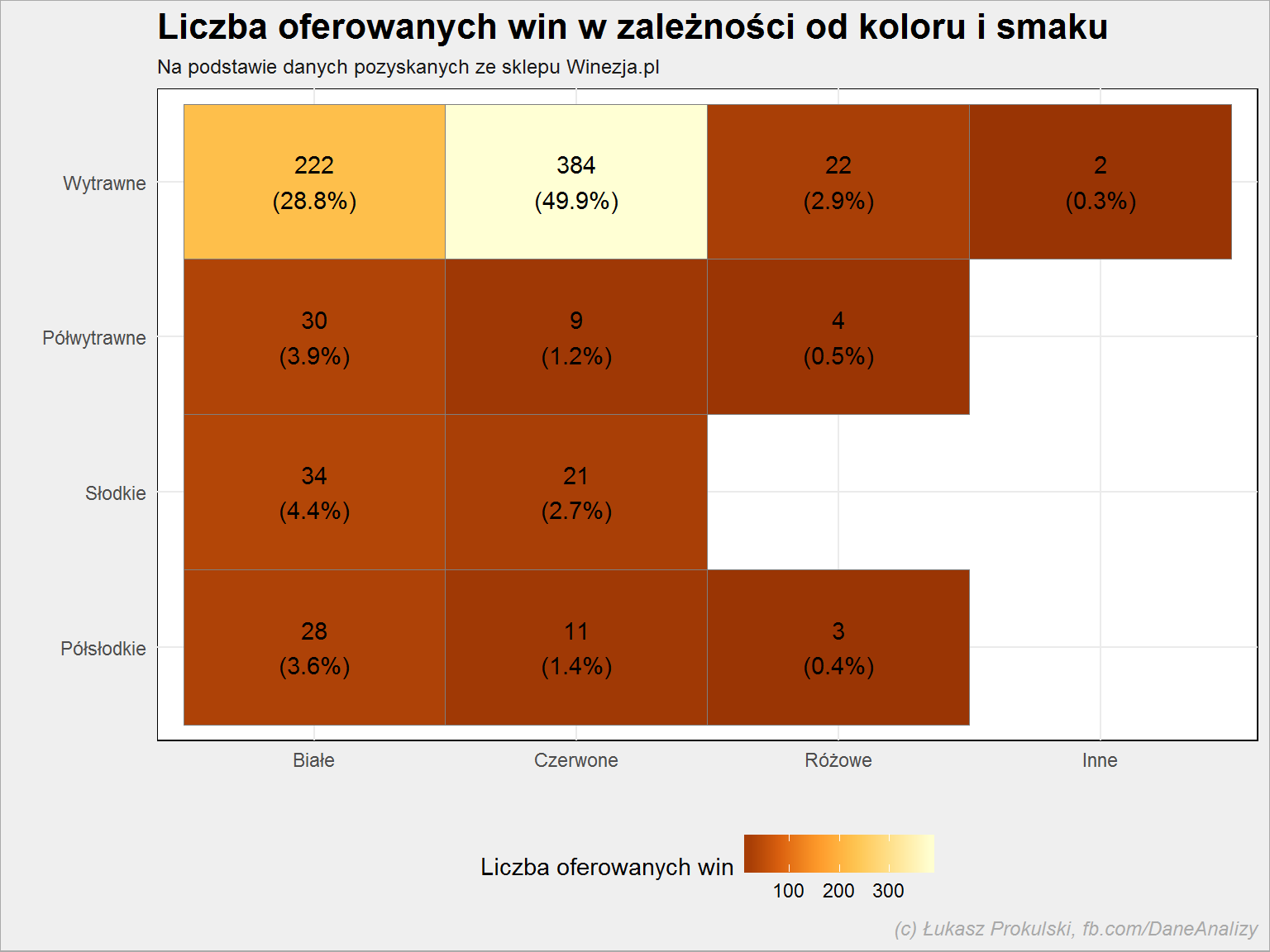
Wiemy już, że 55% wszystkich oferowanych win to wina wytrawne, zaś z powyższego wykresu widzimy, że 49% wszystkich to wytrawne czerwone. Prawie połowa wytrawnych stanowią wina białe. W dużym uproszczeniu można powiedzieć, że:
- wino czerwone to wino wytrawne
- wino białe to też wytrawne
- słodkie są wina białe
- różowe są… wytrawne (i to dla mnie zaskoczenie – sądziłem, że będą to półsłodkie)
Swoją drogą powyższa tabela świetnie nadaje się do przećwiczenia prawa Bayesa. Jeśli mam wino czerwone to z jakim prawdopodobieństwem jest ono słodkie? I tego typu zadania na maturę.
Czy są kraje, gdzie produkuje się więcej win słodkich niż wytrawnych?
|
1 2 3 4 5 6 7 8 9 10 11 12 |
lista_win %>% filter(!is.na(smak)) %>% count(kraj, smak) %>% ungroup() %>% group_by(smak) %>% mutate(p = 100*n/sum(n)) %>% ungroup() %>% ggplot() + geom_tile(aes(smak, kraj, fill = p), color = "gray50") + geom_text(aes(smak, kraj, label = sprintf("%.1f%%", p))) + scale_fill_distiller(palette = "YlOrBr") + theme(legend.position = "bottom") |
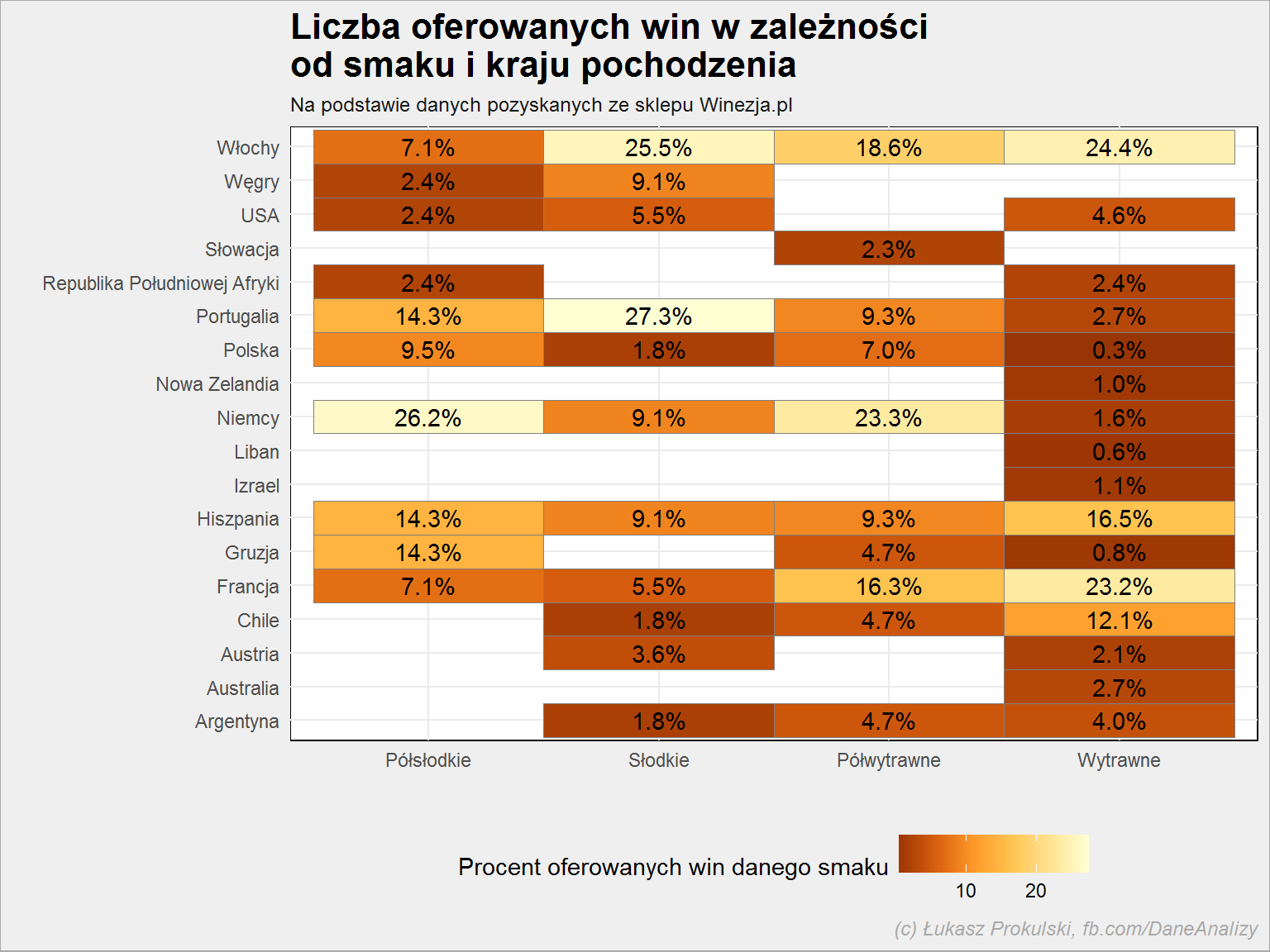
Suma w kolumnie (dla danego smaku) daje 100%. Możemy więc wyczytać, że:
- produkcję win półsłodkich zdominowali Niemcy – ponad 1/4 półsłodkich win oferowanych w sklepie pochodzi z Niemiec
- słodkie pochodzą mniej więcej równomiernie z Portugalii i Włoch
- Niemcy dostarczają też najwięcej win półwytrawnych – ma to sens, klimat jest umiarkowany, daleko od morza, stąd może wynikać wypośrodkowany charakter wina
- najwięcej win wytrawnych w ofercie Winezji pochodzi z Włoch
Zejdźmy teraz poziom niżej – do regionów. Czy region, z którego pochodzi wino ma wpływ na jego smak? Oczywiście tak, ale czy jest to bardzo widoczne – czy są regiony gdzie produkuje się tylko wina słodkie?
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
lista_win %>% filter(!is.na(region), !is.na(smak)) %>% count(kraj, region, smak) %>% ungroup() %>% group_by(kraj, region) %>% mutate(p = sum(n)) %>% ungroup() %>% arrange(p) %>% mutate(region = factor(region, levels = unique(region))) %>% mutate(smak = factor(smak, levels = c("Słodkie", "Półsłodkie", "Półwytrawne", "Wytrawne"))) %>% ggplot() + geom_col(aes(region, n, fill = smak), color = "gray50") + coord_flip() + scale_fill_manual(values = c("Półsłodkie" = "#fdae61", "Słodkie" = "#d7191c", "Półwytrawne" = "#a6d96a", "Wytrawne" = "#1a9641")) + facet_wrap(~kraj, scales = "free", ncol=3) + theme(legend.position = "bottom") |
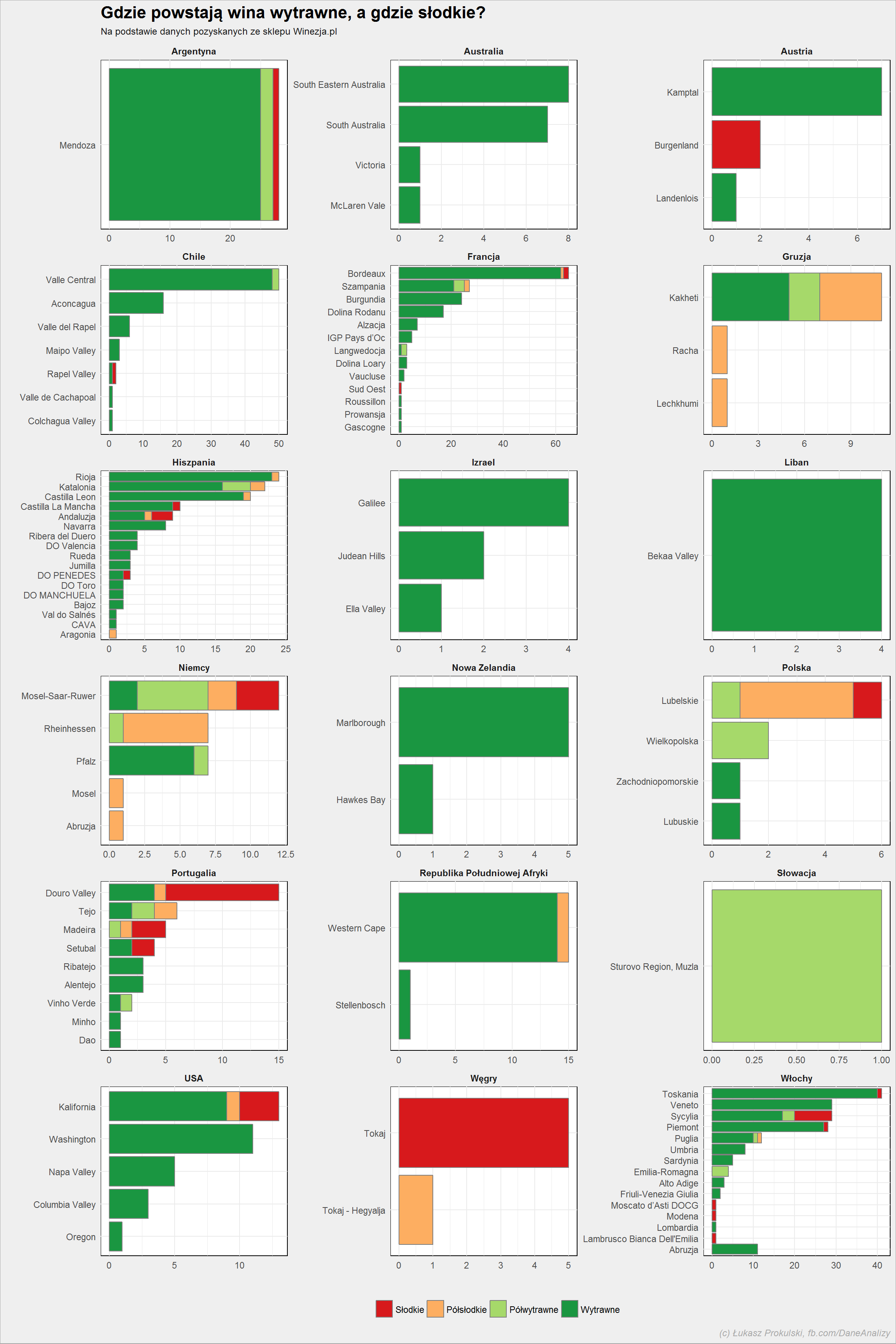
Słodkie wina powstają na Węgrzech (Tokaj) i w Austrii (Burgenland). Najwięcej widać zielonego (czyli win wytrawnych według legendy), ale to wynika również z tego, że w ofercie w ogóle dominują wina wytrawne.
Tyle przeglądu cech. Przejdźmy do cen i (nieco później) ocen.
Czy kraj pochodzenia ma wpływ na cenę butelki?
|
1 2 3 4 5 6 7 8 9 |
lista_win %>% group_by(kraj) %>% mutate(m_cena = median(cena, na.rm = TRUE)) %>% ungroup() %>% arrange(m_cena) %>% mutate(kraj = factor(kraj, levels = unique(kraj))) %>% ggplot() + geom_boxplot(aes(kraj, cena), fill = "#fdae61") + coord_flip() |
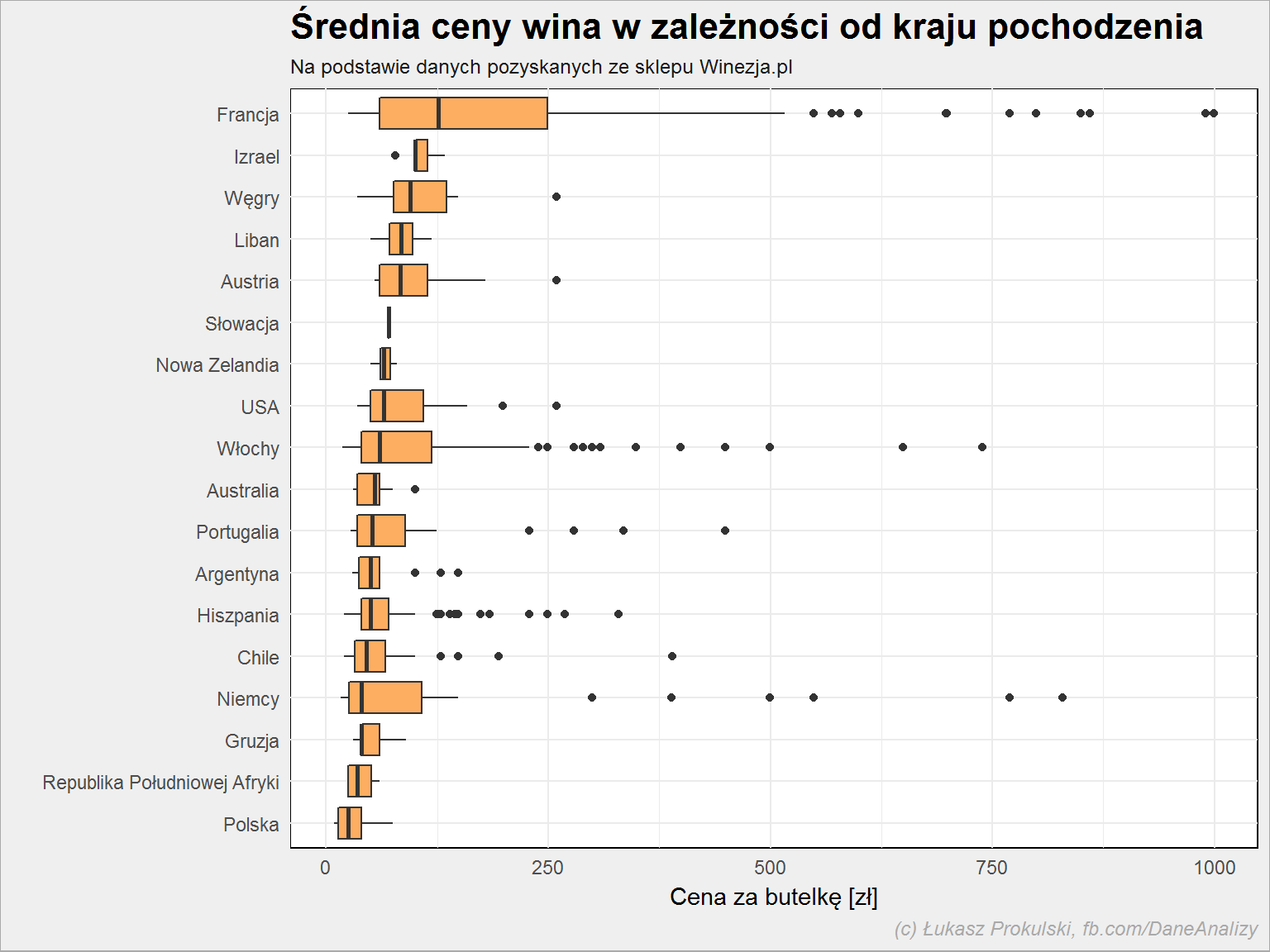
Najtańsze są wina z Polski, co być może da się wytłumaczyć kosztem transportu. Największą medianę cen (i jednocześnie największy ich rozstrzał) mają wina z Francji.
Popularne wina chilijskie mieszczą się w większości w cenie do około 100 zł za butelkę. Spodziewam się, że to jeden z czynników ich popularności. Drugi to (zapewne) ocena. Sprawdźmy jak wypadają te wina według oceny ekspertów:
|
1 2 3 4 5 6 7 8 9 |
lista_win %>% group_by(kraj) %>% mutate(m_ocena = median(expert_rating, na.rm = TRUE)) %>% ungroup() %>% arrange(m_ocena) %>% mutate(kraj = factor(kraj, levels = unique(kraj))) %>% ggplot() + geom_boxplot(aes(kraj, expert_rating), fill = "#fdae61") + coord_flip() |
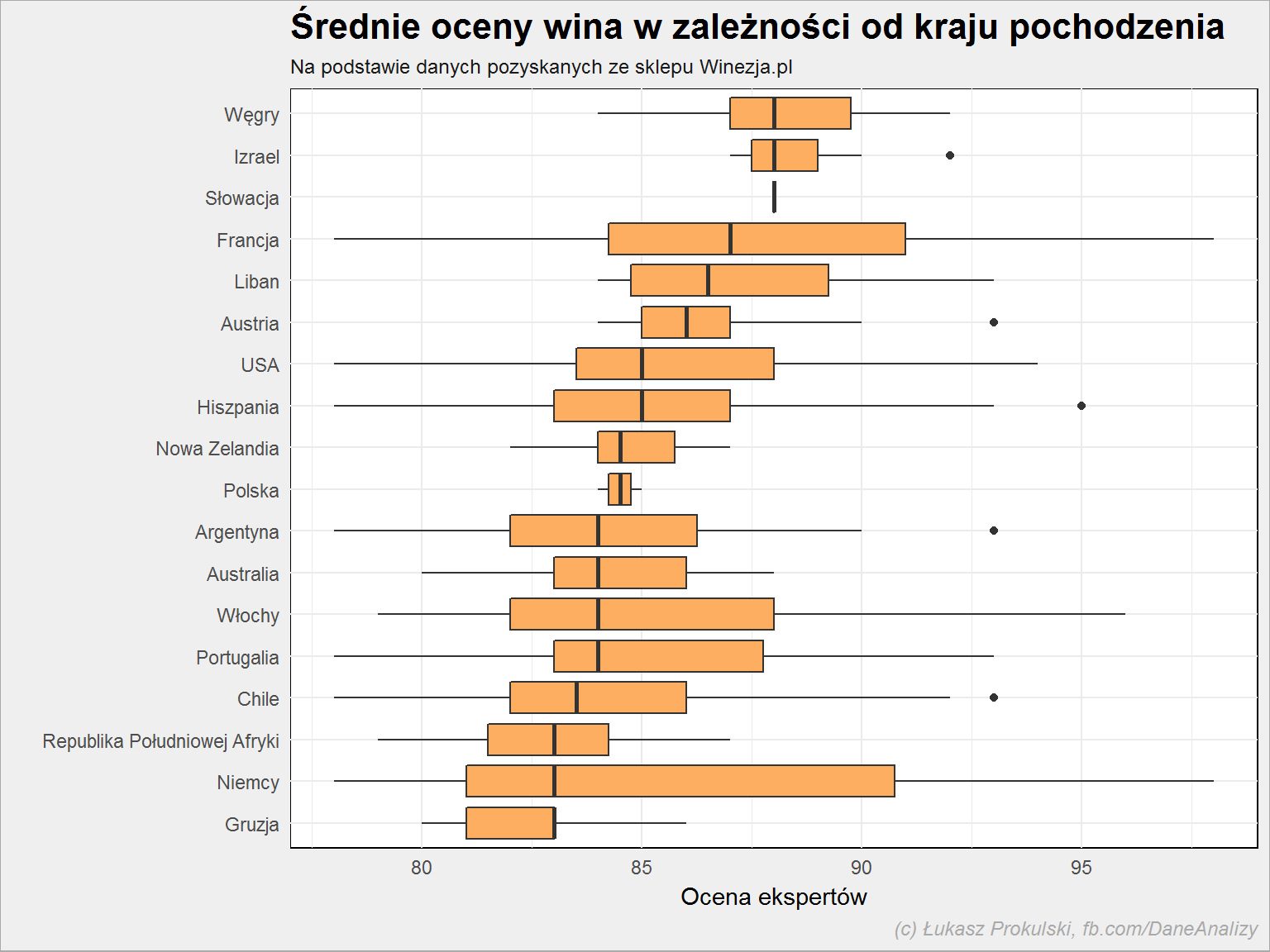
I tutaj mamy ciekawostkę: wino z Chile jest średnio (dokładniej: medianą) gorzej ocenione niż wino z Polski. Zaś Francja nie jest wcale najlepsza – lepsze są węgierskie tokaje.
Czy smak wina ma wpływ na cenę? Droższe są słodkie czy wytrawne?
|
1 2 3 4 5 6 7 8 9 10 |
lista_win %>% filter(!is.na(smak)) %>% group_by(smak) %>% mutate(m_cena = median(cena, na.rm = TRUE)) %>% ungroup() %>% arrange(m_cena) %>% mutate(smak = factor(smak, levels = unique(smak))) %>% ggplot() + geom_boxplot(aes(smak, cena), fill = "#fdae61") + coord_flip() |
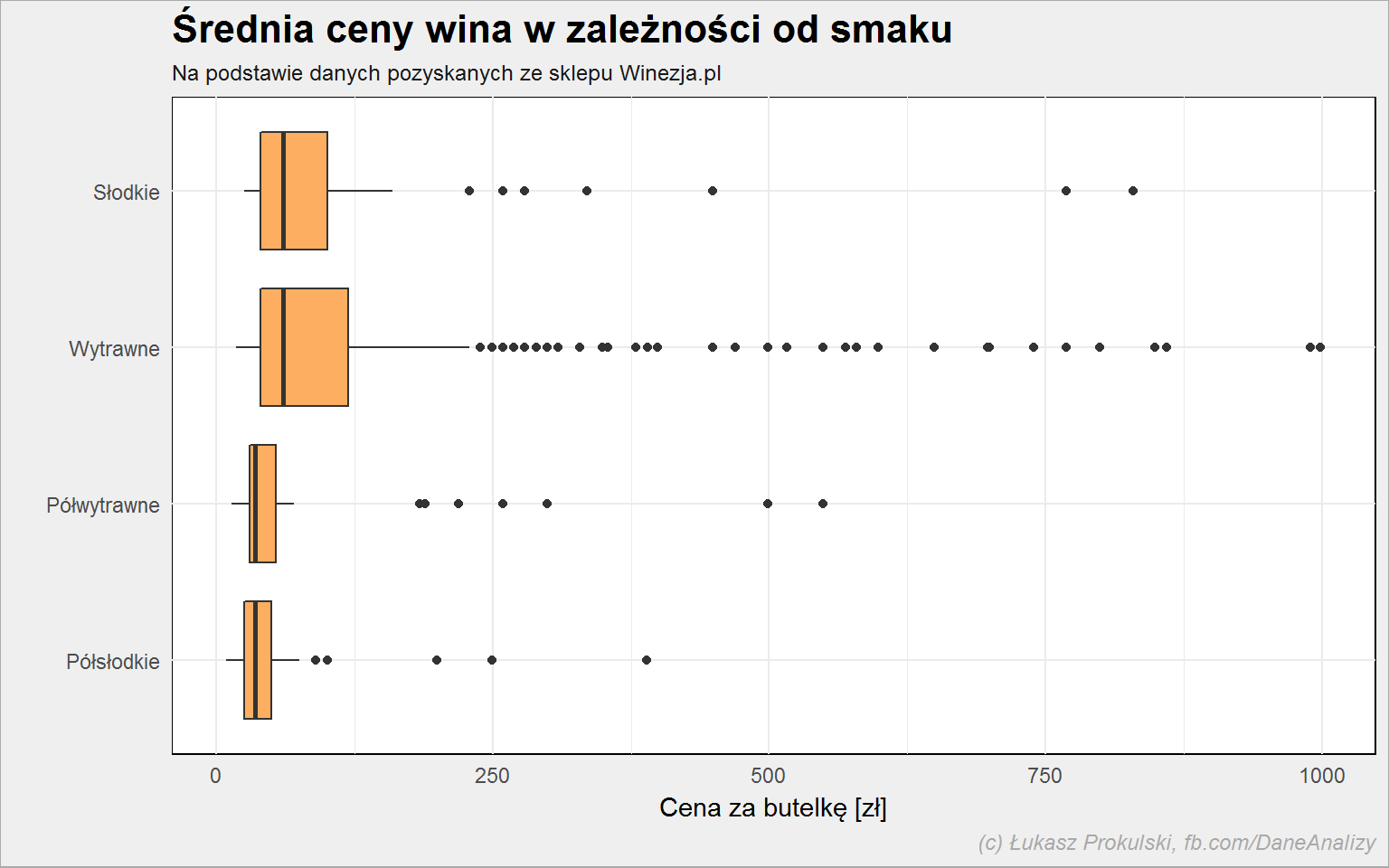
Patrząc na medianę to słodkie wina są nieznacznie droższe od wytrawnych. Widać wyraźnie różnicę pomiędzy smakami pośrednimi (półsłodkie i półwytrawne) a pełnymi.
Porównajmy jeszcze cenę i ocenę. Czy lepsze oznacza droższe?
|
1 2 3 4 5 |
lista_win %>% filter(!is.na(expert_rating), !is.na(smak)) %>% ggplot() + geom_smooth(aes(expert_rating, cena, color = smak), show.legend = FALSE) + facet_wrap(~smak, ncol = 2) |
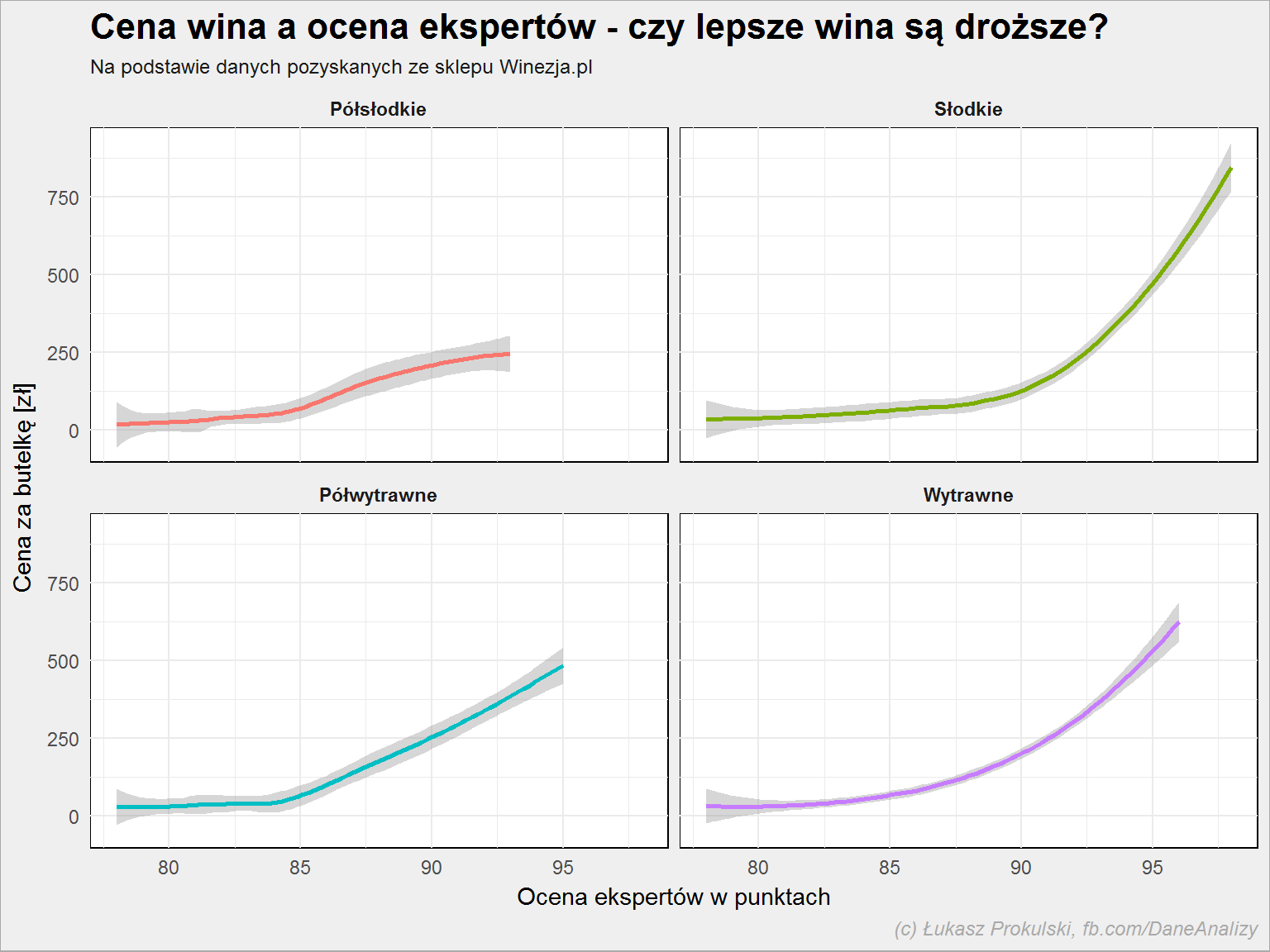
Jest tak jak można się spodziewać: za jakość należy zapłacić. To naturalne prawo rynku. Do wyboru wina dobrego i taniego (oraz taniego i dobrego) jeszcze wrócimy.
Czy eksperci mają jakieś preferencje jeśli chodzi o smak?
|
1 2 3 4 5 |
lista_win %>% filter(!is.na(smak)) %>% ggplot() + geom_boxplot(aes(smak, expert_rating), fill = "#fdae61") + coord_flip() |
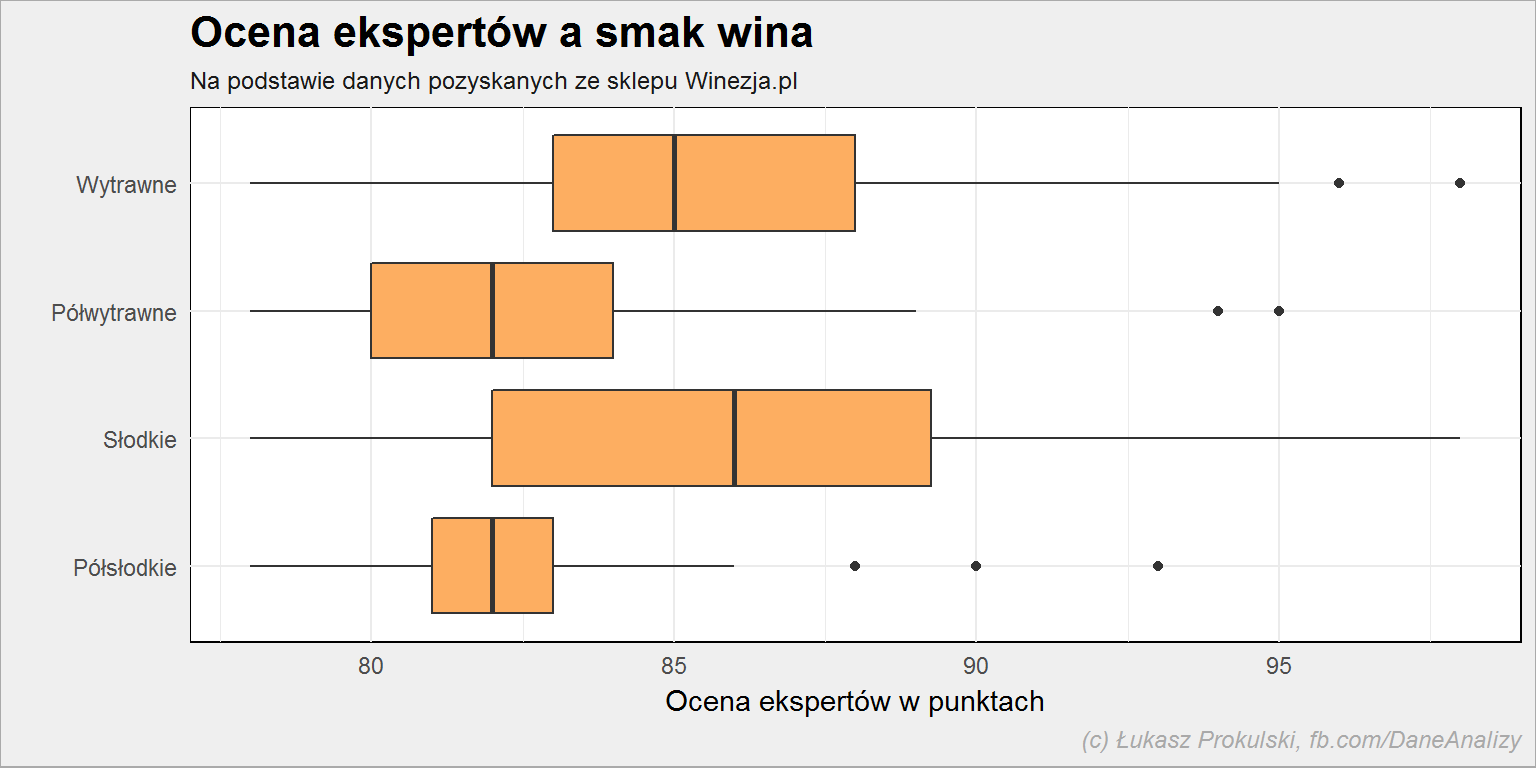
Znowu: wina wyraziste (nie jakieś pół-) są oceniane lepiej. Różnica jest na poziomie kilku punktów (w skali 1-100, gdzie najniżej oceniane wino w naszym zbiorze ma ocenę 78, a najwyżej – 98), co wydaje się być całkiem sporą wartością.
A teraz klucz do rozwoju biznesu. Nie wiem czy sklep Winezja.pl prowadzi takie analizy. Jeśli nie – zrobiłem to za nich (gratis). Z jednej strony znamy podaż (ofertę sklepu) i wiemy, że najwięcej oferowanych jest win wytrawnych (prawie 82%), ale czy też takich sprzedaje się najwięcej?
|
1 2 3 4 5 6 |
lista_win %>% filter(!is.na(smak)) %>% ggplot() + geom_boxplot(aes(smak, popularnosc), fill = "#fdae61") + coord_flip() + scale_y_log10() |
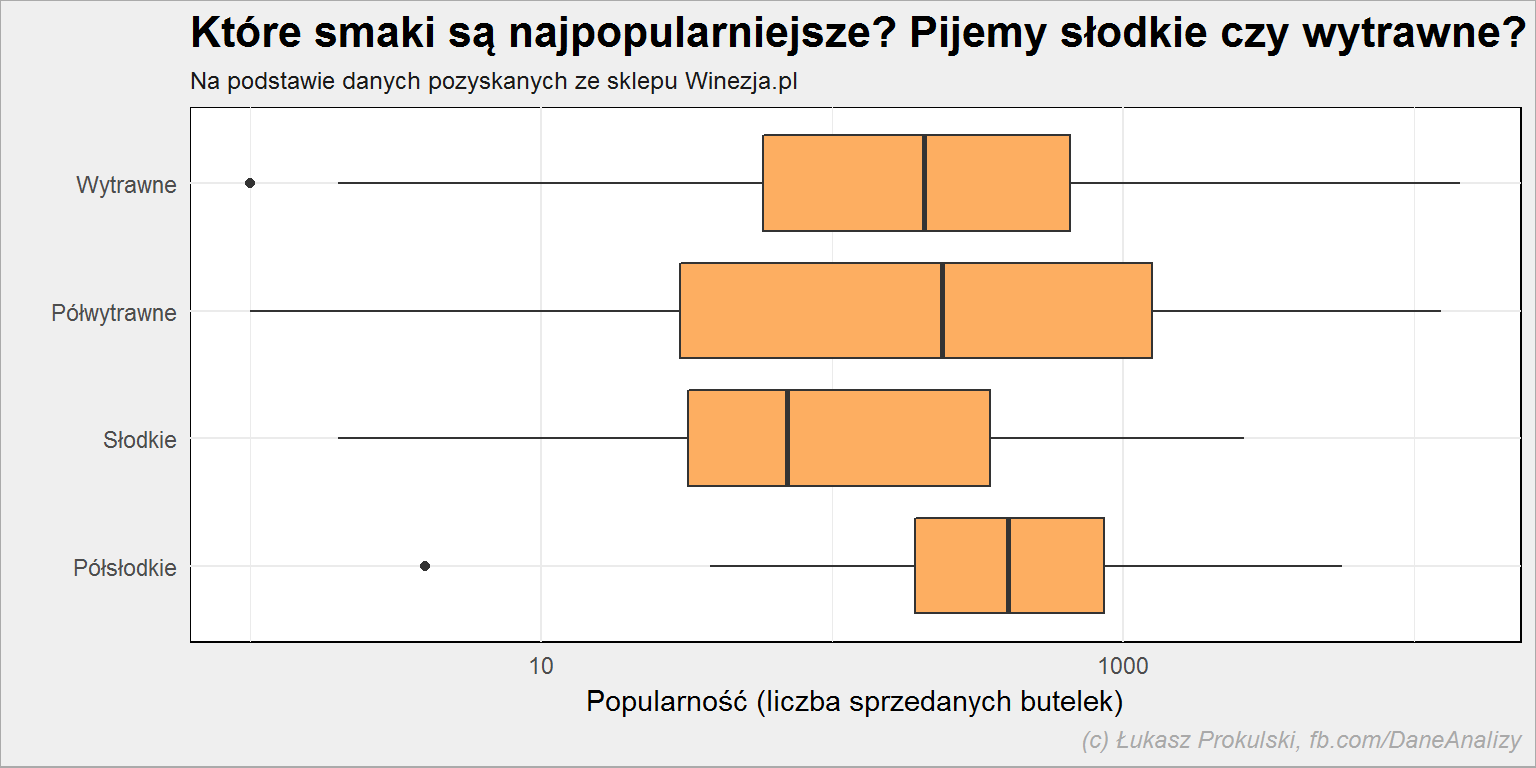
Wykres może być mylący. Grupuje on wina po smakach i pokazuje rozstrzał liczby sprzedanych butelek. Na pierwszy rzut oka widać, że mediana dla półwytrawnych win jest większa niż win wytrawnych, a w ogóle największa dla win słodkich. Czy to znaczy, że słodkich sprzedaje się najwięcej? Nie.
Zobaczmy to w formie tabeli, zestawiając udział procentowy smaków ze względu na liczbę sprzedanych butelek (ich sumę dla danego smaku) po stronie popytowej oraz liczbę win (oferowanych) po stronie podażowej:
|
1 2 3 4 5 6 7 8 |
lista_win %>% filter(!is.na(smak)) %>% group_by(smak) %>% summarise(popyt = sum(popularnosc, na.rm = T), podaz = n()) %>% ungroup() %>% mutate(popyt_p = round(100*popyt/sum(popyt), 1), podaz_p = round(100*podaz/sum(podaz), 1)) |
| Smak | Popyt | Podaż | Popyt % | Podaż % |
|---|---|---|---|---|
| Półsłodkie | 36918 | 42 | 7.7 | 5.5 |
| Słodkie | 14181 | 55 | 2.9 | 7.1 |
| Półwytrawne | 51527 | 43 | 10.7 | 5.6 |
| Wytrawne | 379527 | 630 | 78.7 | 81.8 |
Podaż i popyt nie są idealnie zrównoważone (widać to szczególnie w przypadku win półwytrawnych). Ale może tak powinno być? Najwięcej oferowanych jest tych, które kupują się najlepiej – wśród kategorii “wina wytrawne” mamy największy wybór.
Schodząc dodatkowo na poziom koloru (wystarczy dodać w grupowaniu kolor) widać podobną równowagę. Jeśli miałbym coś sugerować to dodanie win czerwonych półwytrawnych: spożycie to 5.5%, a oferta to 1.2%.
No właśnie – co pijemy? Jak rozkłada się popularność (mierzona liczbą sprzedanych butelek) na poszczególne smaki i kolory?
|
1 2 3 4 5 6 7 8 9 10 11 |
lista_win %>% filter(!is.na(smak), !is.na(kolor)) %>% group_by(smak, kolor) %>% summarise(n = sum(popularnosc, na.rm = T)) %>% ungroup() %>% mutate(p = 100*n/sum(n)) %>% ggplot() + geom_tile(aes(kolor, smak, fill = n), color = "gray80") + geom_text(aes(kolor, smak, label = sprintf("%.1f%%", p))) + scale_fill_distiller(palette = "YlOrBr") + theme(legend.position = "bottom") |
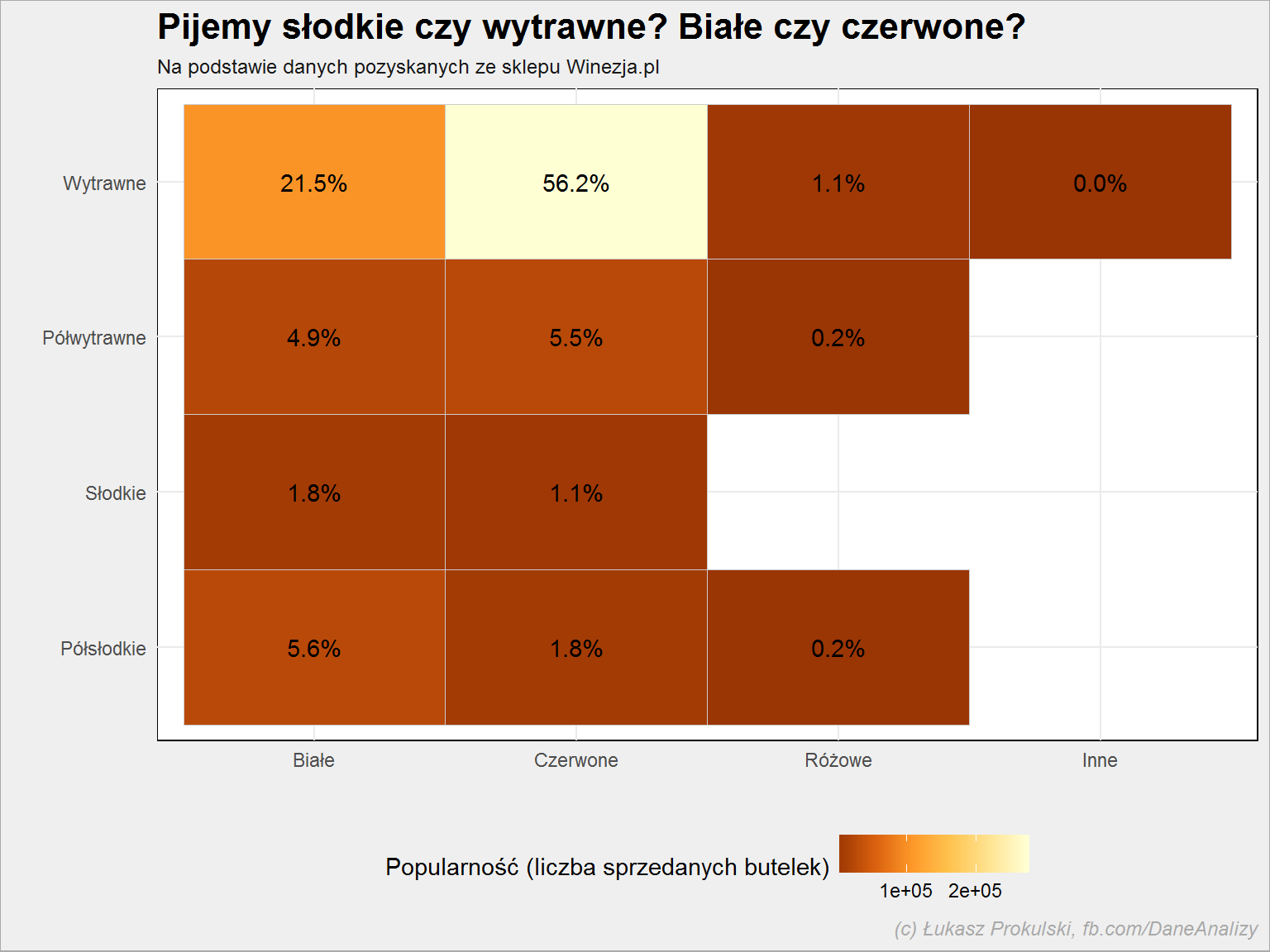
Wróćmy teraz do ocen. Na początek oceny ekspertów, tym razem podzielone według smaków i kraju pochodzenia wina:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
lista_win %>% filter(!is.na(smak), !is.na(expert_rating)) %>% group_by(kraj, smak) %>% summarise(n = mean(expert_rating, na.rm = TRUE)) %>% ungroup() %>% group_by(smak) %>% mutate(max_n = max(n)) %>% ungroup() %>% ggplot() + geom_col(aes(kraj, n, fill = n == max_n), color = "gray50", show.legend = FALSE) + scale_fill_manual(values = c("TRUE" = "#d7191c", "FALSE" = "#a6d96a")) + coord_flip() |
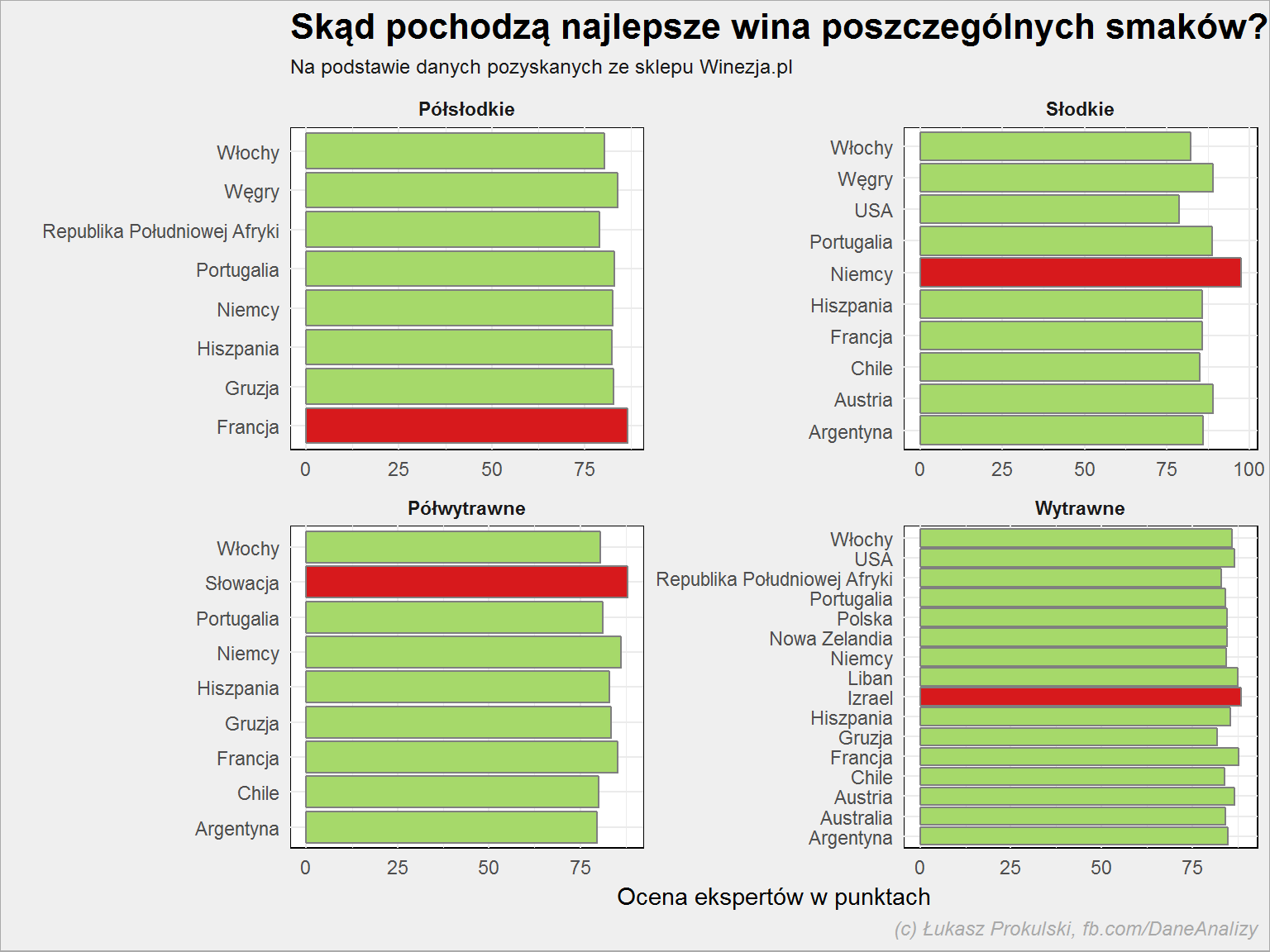
Na czerwono oznaczone są te kraje, dla których ocena była najwyższa. Sprawdźmy w detalach, po trzy kraje dla danego smaku:
|
1 2 3 4 5 6 7 8 9 10 11 |
lista_win %>% filter(!is.na(smak), !is.na(expert_rating)) %>% group_by(kraj, smak) %>% summarise(n = mean(expert_rating, na.rm = TRUE)) %>% ungroup() %>% group_by(smak) %>% top_n(3, n) %>% ungroup() %>% arrange(smak, desc(n)) %>% select(smak, kraj, n) %>% mutate(n = round(n, 1)) |
| Smak | Kraj | Ocena |
|---|---|---|
| Półsłodkie | Francja | 86.7 |
| Półsłodkie | Węgry | 84.0 |
| Półsłodkie | Portugalia | 83.2 |
| Słodkie | Niemcy | 97.7 |
| Słodkie | Austria | 89.0 |
| Słodkie | Węgry | 89.0 |
| Półwytrawne | Słowacja | 88.0 |
| Półwytrawne | Niemcy | 86.2 |
| Półwytrawne | Francja | 85.3 |
| Wytrawne | Izrael | 88.6 |
| Wytrawne | Francja | 87.7 |
| Wytrawne | Liban | 87.5 |
Ta Słowacja (półwytrawne) wygląda interesująco – jakie to wino?
|
1 2 3 4 |
lista_win %>% filter(kraj == "Słowacja", smak == "Półwytrawne") %>% filter(expert_rating == max(expert_rating, na.rm = TRUE)) %>% select(nazwa, kolor, rocznik, producent, cena, expert_rating) |
| Nazwa | Kolor | Rocznik | Producent | Cena [zł] | Ocena |
|---|---|---|---|---|---|
| Chateau Bela Riesling Sturovo Region Muzla | Białe | 2015 | Chateau Bela S.R.O. | 69.99 | 88 |
W sklepie mamy również oceny rozbite na poszczególne składowe: smak, gładkość, budowa i aromat. Swoją drogą kod strony jest nieco zakręcony w tym miejscu – dla zainteresowanych polecam prześledzić skrypt pobierający dane. Ja to wygląda w rozbiciu na gatunki (smaki)?
|
1 2 3 4 5 6 7 8 9 10 11 |
lista_win %>% select(c(2, 3, 25:28)) %>% filter(!is.na(smak)) %>% gather(key, val, -kolor, -smak) %>% group_by(kolor, smak, key) %>% summarise(n = mean(val)) %>% mutate(key = gsub("ocena_", "", key)) %>% ggplot() + geom_point(aes(n, key), size = 3, color = "#d7191c") + scale_x_continuous(limits = c(0, 5)) + facet_grid(kolor~smak) |
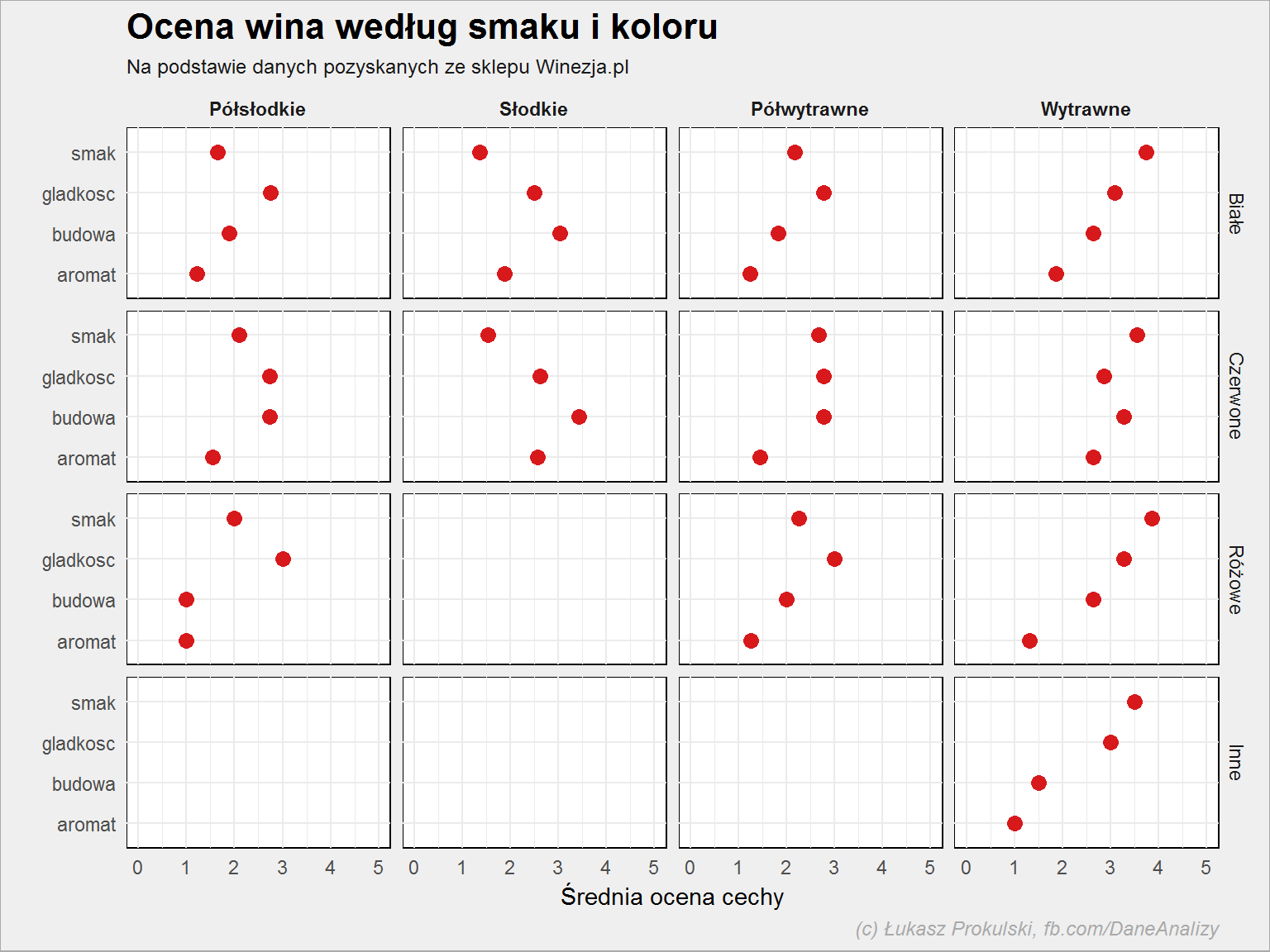
Najsmaczniejsze są wina wytrawne (jak pamiętacie w ogólnej ocenie są również dobrze oceniane) i to bez względu na kolor. Jakie wina są najlepsze w danej kategorii oceny? Zróbmy tabelę:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
lista_win %>% select(c(2, 3, 25:28)) %>% filter(!is.na(smak)) %>% gather(key, val, -kolor, -smak) %>% group_by(kolor, smak, key) %>% summarise(n = mean(val)) %>% mutate(key = gsub("ocena_", "", key)) %>% group_by(key) %>% filter(n == max(n)) %>% mutate(n = round(n, 1)) %>% ungroup() %>% select(key, kolor, smak, n) |
| Cecha | Kolor | Smak | Ocena |
|---|---|---|---|
| budowa | Czerwone | Słodkie | 3.4 |
| aromat | Czerwone | Wytrawne | 2.6 |
| gładkość | Różowe | Wytrawne | 3.3 |
| smak | Różowe | Wytrawne | 3.9 |
Odejdźmy teraz od koloru w zamian za kraj:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
lista_win %>% select(c(3, 6, 25:28)) %>% filter(!is.na(smak)) %>% gather(key, val, -smak, -kraj) %>% filter(val != 0) %>% group_by(smak, kraj, key) %>% summarise(n = mean(val)) %>% ungroup() %>% group_by(key) %>% mutate(n_max = max(n)) %>% ungroup() %>% mutate(key = gsub("ocena_", "", key)) %>% ggplot() + geom_tile(aes(smak, kraj, fill = n), color = "gray80") + geom_text(aes(smak, kraj, label = round(n, 1), color = (n == n_max)), size = 2.9, show.legend = FALSE) + scale_fill_distiller(palette = "PuBu") + scale_color_manual(values = c("TRUE" = "red", "FALSE" = "black")) + facet_wrap(~key) + theme(legend.position = "bottom") |

Jeśli chcesz najbardziej aromatyczne wino – kup chilijskie słodkie. Najsmaczniejsze – austriackie wytrawne.
Teraz przełóżmy te same dane w inną formę:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
lista_win %>% select(c(3, 6, 25:28)) %>% filter(!is.na(smak)) %>% gather(key, val, -smak, -kraj) %>% filter(val != 0) %>% group_by(smak, kraj, key) %>% summarise(n = mean(val)) %>% ungroup() %>% mutate(key = gsub("ocena_", "", key)) %>% group_by(smak, key) %>% top_n(1, n) %>% ggplot() + geom_jitter(aes(key, smak, color = kraj), width = 0.15, height = 0.15, size = 5) + scale_color_brewer(palette = "Paired") |
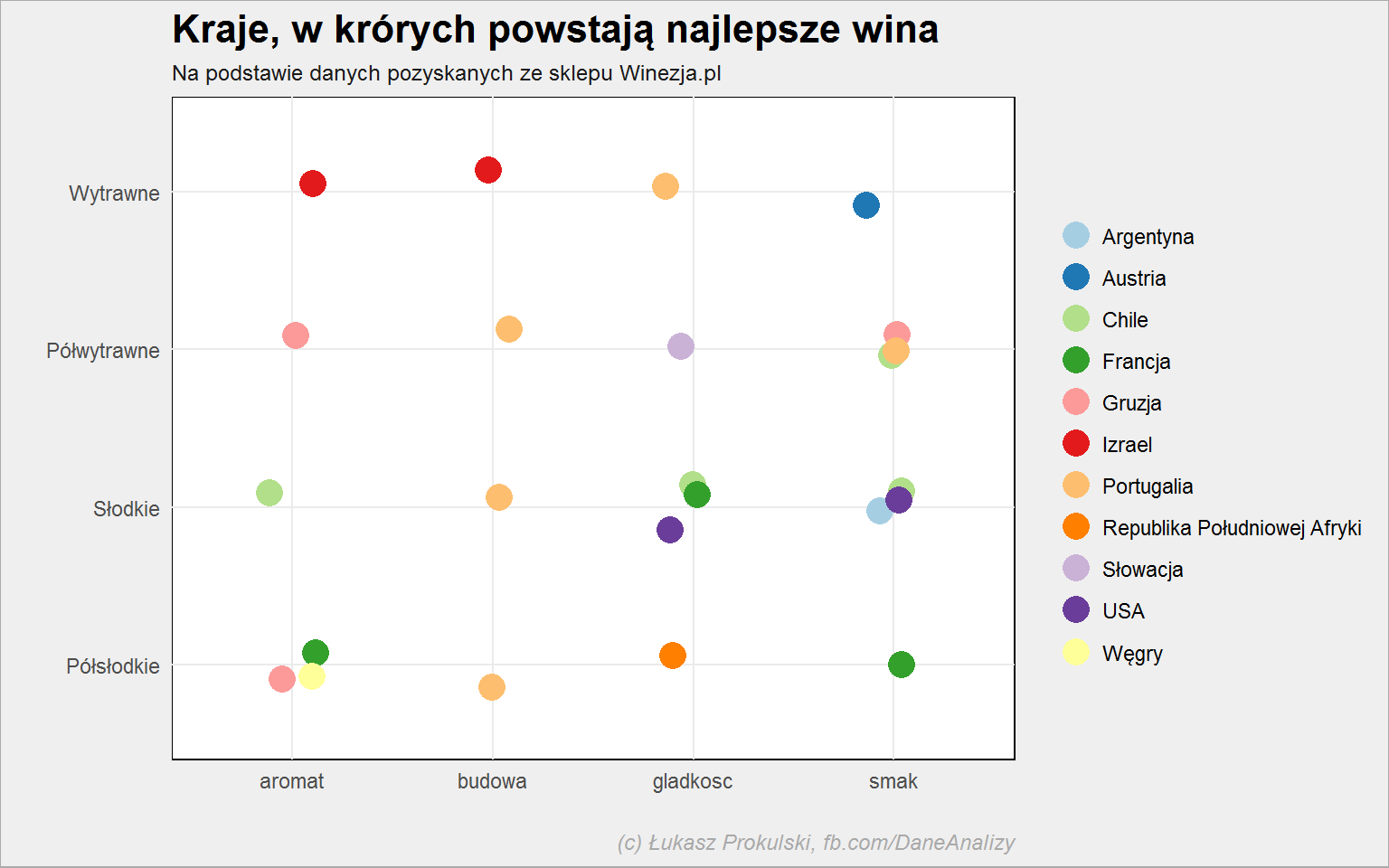
Celowałbym w Portugalię, bez względu na rodzaj wina :)
Do każdego z win w sklepie mamy podaną zalecaną temperaturę podawania. Nauczmy się więc przy okazji czegoś i dowiedzmy w jakiej temperaturze podawać wina? Biorąc pod uwagę najczęściej występującą temperaturę dla każdego z gatunków i kolorów:
|
1 2 3 4 5 6 7 8 9 10 11 |
lista_win %>% filter(!is.na(smak)) %>% count(smak, kolor, temp_podawania) %>% ungroup() %>% group_by(smak, kolor) %>% arrange(desc(n)) %>% mutate(rown = row_number()) %>% top_n(-1, rown) %>% ungroup() %>% select(kolor, smak, temp_podawania) %>% spread(kolor, temp_podawania, fill = " ") |
| Smak | Białe | Czerwone | Różowe | Inne |
|---|---|---|---|---|
| Półsłodkie | 8°C | 14°C | 10°C | |
| Słodkie | 8-10°C | 18°C | ||
| Półwytrawne | 10°C | 14-16°C | 10°C | |
| Wytrawne | 10°C | 18°C | 10°C | 12°C |
Zasada jest prosta: zawsze około 10 stopni Celsiusza, chyba że wino czerwone to nieco cieplejsze (16 stopni będzie ok).
Przejdźmy teraz do roczników, a raczej informacji od kiedy wina są dostępne w sklepie:
|
1 2 3 4 5 6 7 8 |
lista_win %>% filter(!is.na(dostpene_od)) %>% ggplot() + geom_density(aes(dostpene_od), color = "gray50", fill = "#a6d96a") + labs(title = "Od kiedy wina dostępne są w sklepie?", subtitle = "Na podstawie danych pozyskanych ze sklepu Winezja.pl", x = "", y = "", color = "", fill = "", caption = "(c) Łukasz Prokulski, fb.com/DaneAnalizy") |
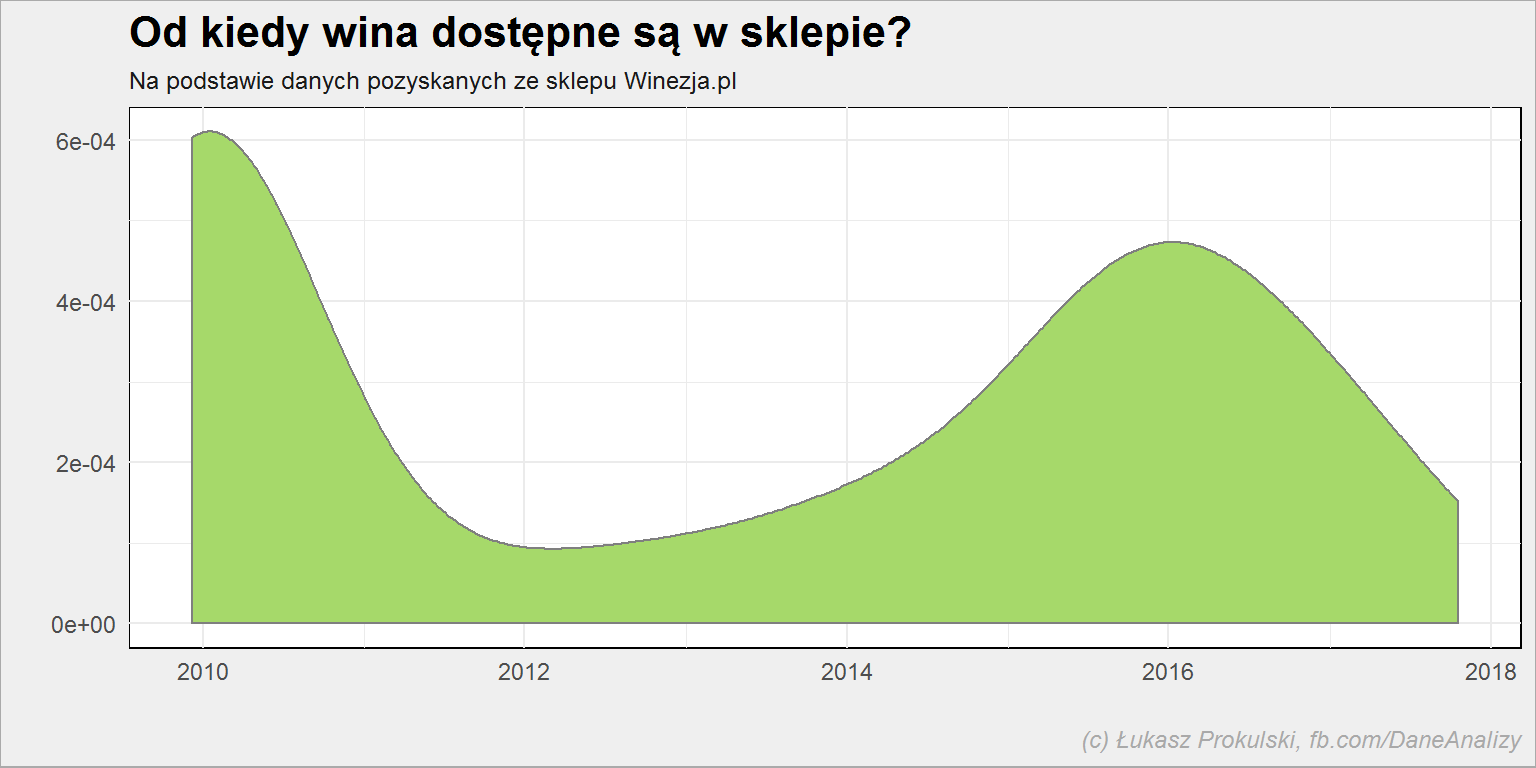
Widać tutaj historię zdobywania nowych pozycji w ofercie (tak sobie to tłumaczę). Nie wiem kiedy powstał sklep, można sądzić że w 2010 roku. W 2016 dotarła druga fala nowych zakupów (kontraktów).
Popatrzmy na roczniki oferowanych win:
|
1 2 3 4 |
lista_win %>% filter(!is.na(rocznik)) %>% ggplot() + geom_density(aes(rocznik), color = "gray50", fill = "#a6d96a") |
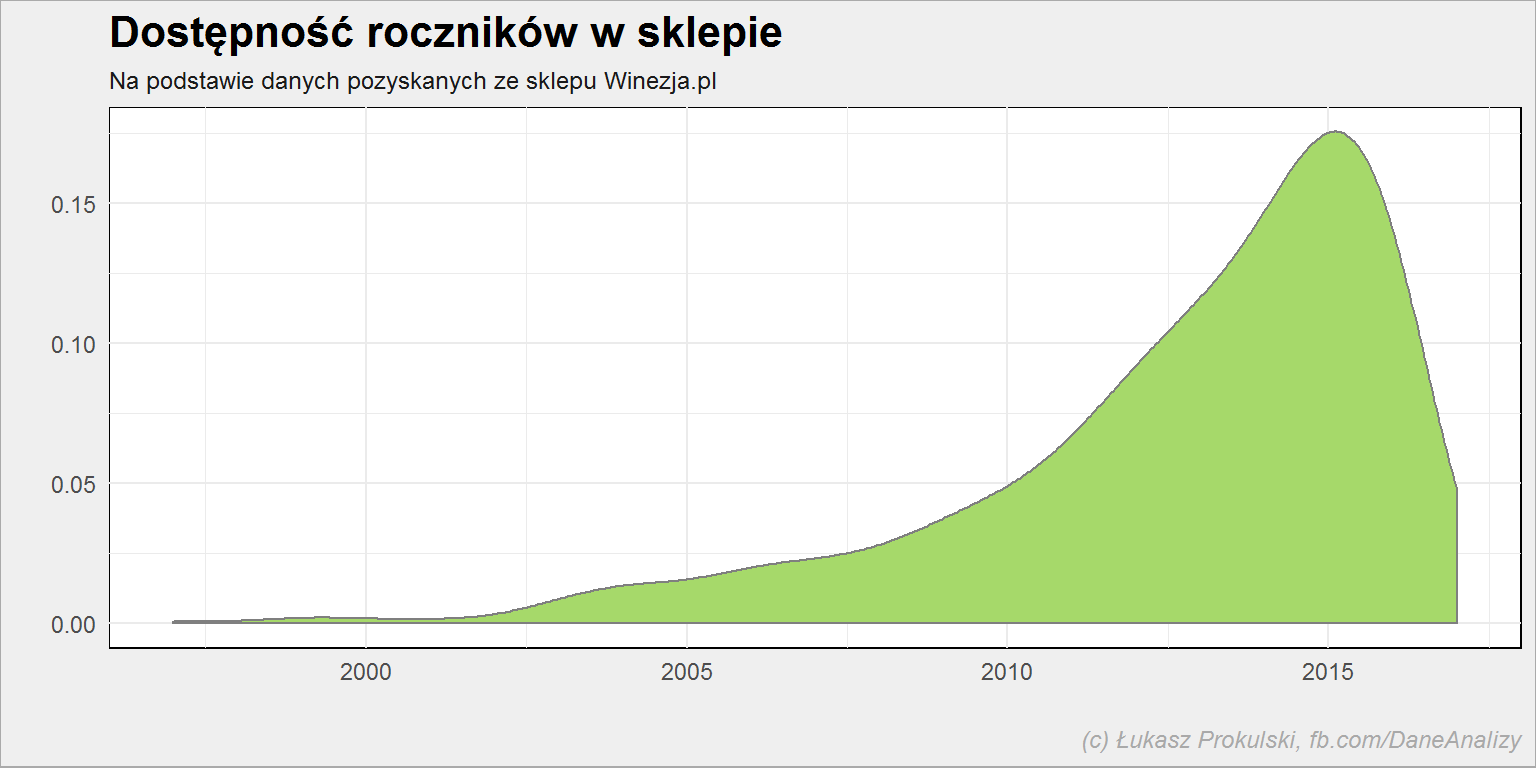
Najwięcej w ofercie jest win z rocznika 2015. Ma to swoje uzasadnienie, zapewne w cenie jaki dostępności u producentów.
Czy wina długo dostępne są bardziej popularne?
|
1 2 3 4 5 |
lista_win %>% mutate(popularnosc = as.numeric(popularnosc)) %>% filter(!is.na(dostpene_od), !is.na(popularnosc)) %>% ggplot() + geom_smooth(aes(dostpene_od, popularnosc), color = "#a6d96a") |
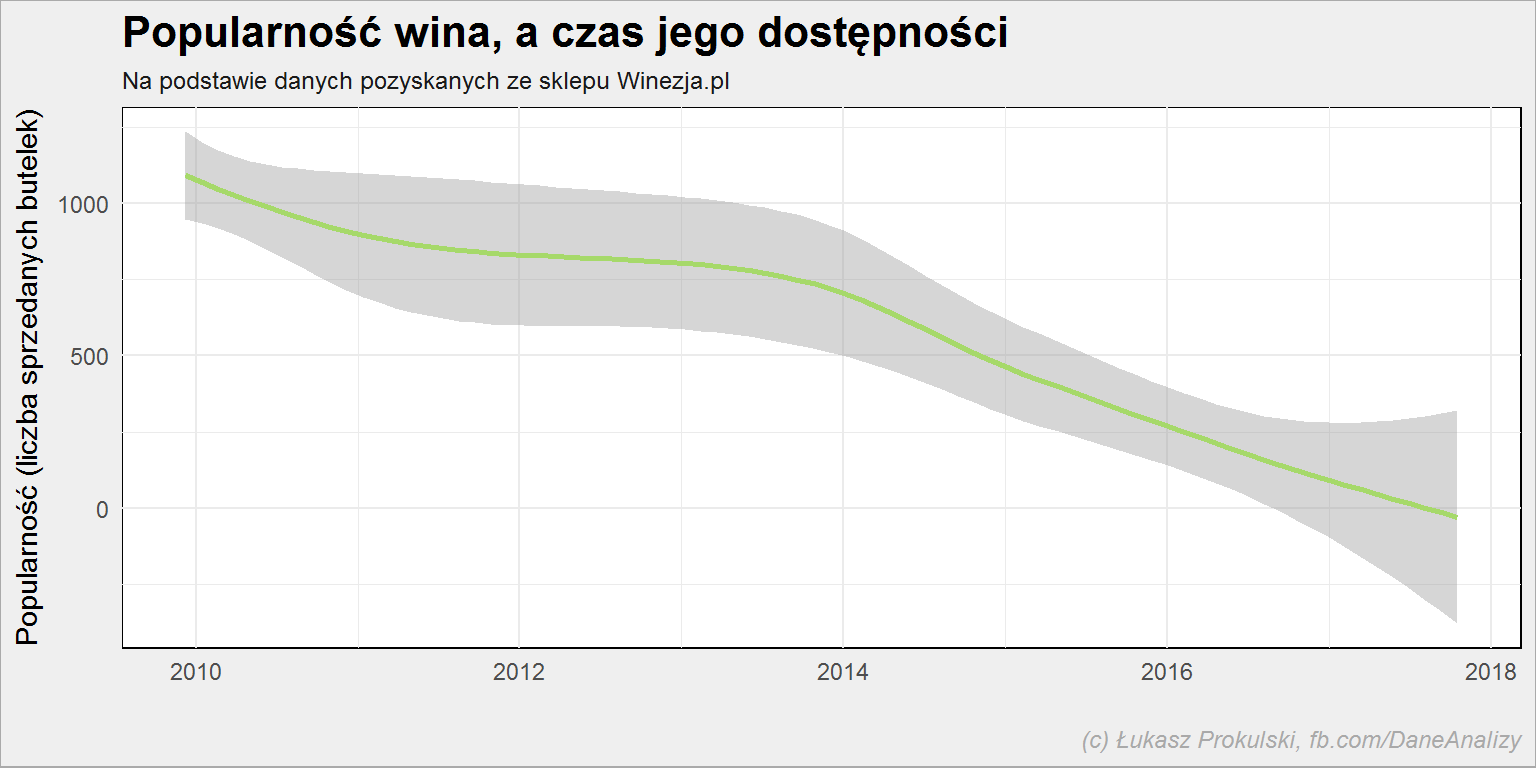
To nie powinno zaskakiwać: towary, które są od długiego czasu oferowane zdążyły się sprzedać. A jeśli się sprzedają to nie zostają wycofane.
Sprawdźmy czy cena ma przełożenie na popularność wina?
|
1 2 3 4 5 |
lista_win %>% mutate(popularnosc = as.numeric(popularnosc)) %>% ggplot() + geom_smooth(aes(cena, popularnosc), color = "#a6d96a") + scale_x_log10() |
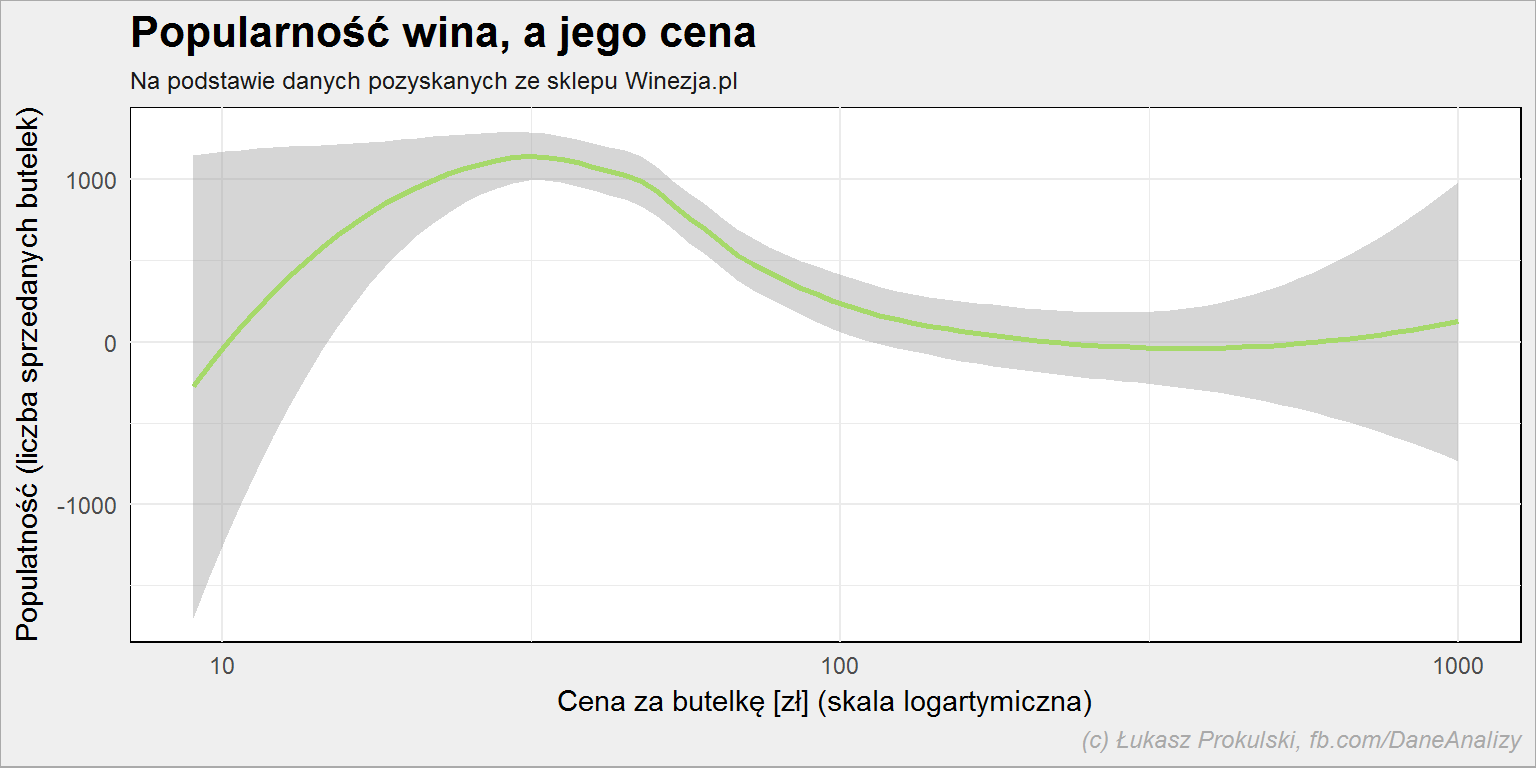
Oczywiście, że ma. Mało jest osób, które są w stanie wydać dużo na wino – większość Polaków robi tego typu zakupy w marketach, Lidlach czy Biedronkach, a tam ceny są w okolicy 20-30 złotych. Jeśli ktoś szuka innego wina robi to w sklepie internetowym (albo specjalistycznym stacjonarnym). A jeśli szuka to znaczy, że mu zależy i jest w stanie zapłacić nieco więcej niż w markecie.
|
1 2 3 4 5 6 7 8 |
lista_win %>% filter(cena <= 200) %>% mutate(popularnosc = as.numeric(popularnosc)) %>% mutate(cena = cut(cena, breaks = seq(0, 200, 10))) %>% mutate(cena = fct_rev(cena)) %>% ggplot() + geom_col(aes(cena, popularnosc), fill = "#a6d96a") + coord_flip() |
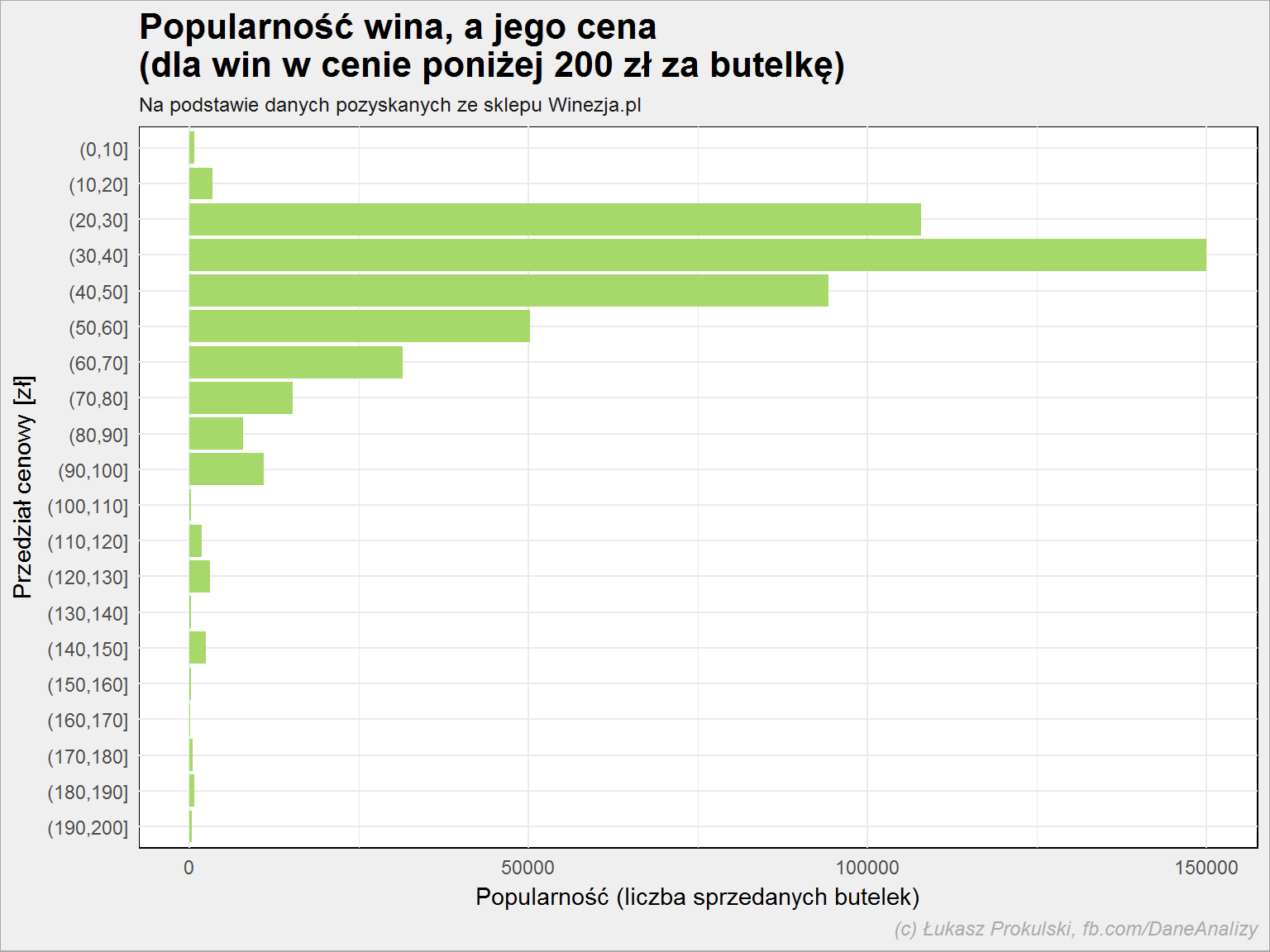
Z powyższych przyczyn najwięcej sprzedaje się win w cenie w okolicach 30-40 złotych. Jest to kompromis pomiędzy jakością, ceną i narzutem związanym z kosztem dostawy.
Przejdźmy teraz do szczepów winorośli. Bo przecież wszystko od tego zależy. Jakie szczepy są najpopularniejsze? Od razu w podziale na kraj pochodzenia:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
lista_win %>% select(kraj, szczep) %>% separate(szczep, paste0("Szczep", 1:8), sep = ",") %>% gather(dummy, Szczep, -kraj) %>% filter(!is.na(Szczep)) %>% select(-dummy) %>% rowwise() %>% mutate(Szczep = str_trim(str_replace(Szczep,"\\(.*\\)", ""))) %>% ungroup() %>% count(kraj, Szczep, sort = T) %>% top_n(3, n) %>% ungroup() %>% ggplot() + geom_col(aes(Szczep, n), color = "gray50", fill = "#a6d96a") + coord_flip() + facet_wrap(~kraj, scales="free", ncol = 3) |
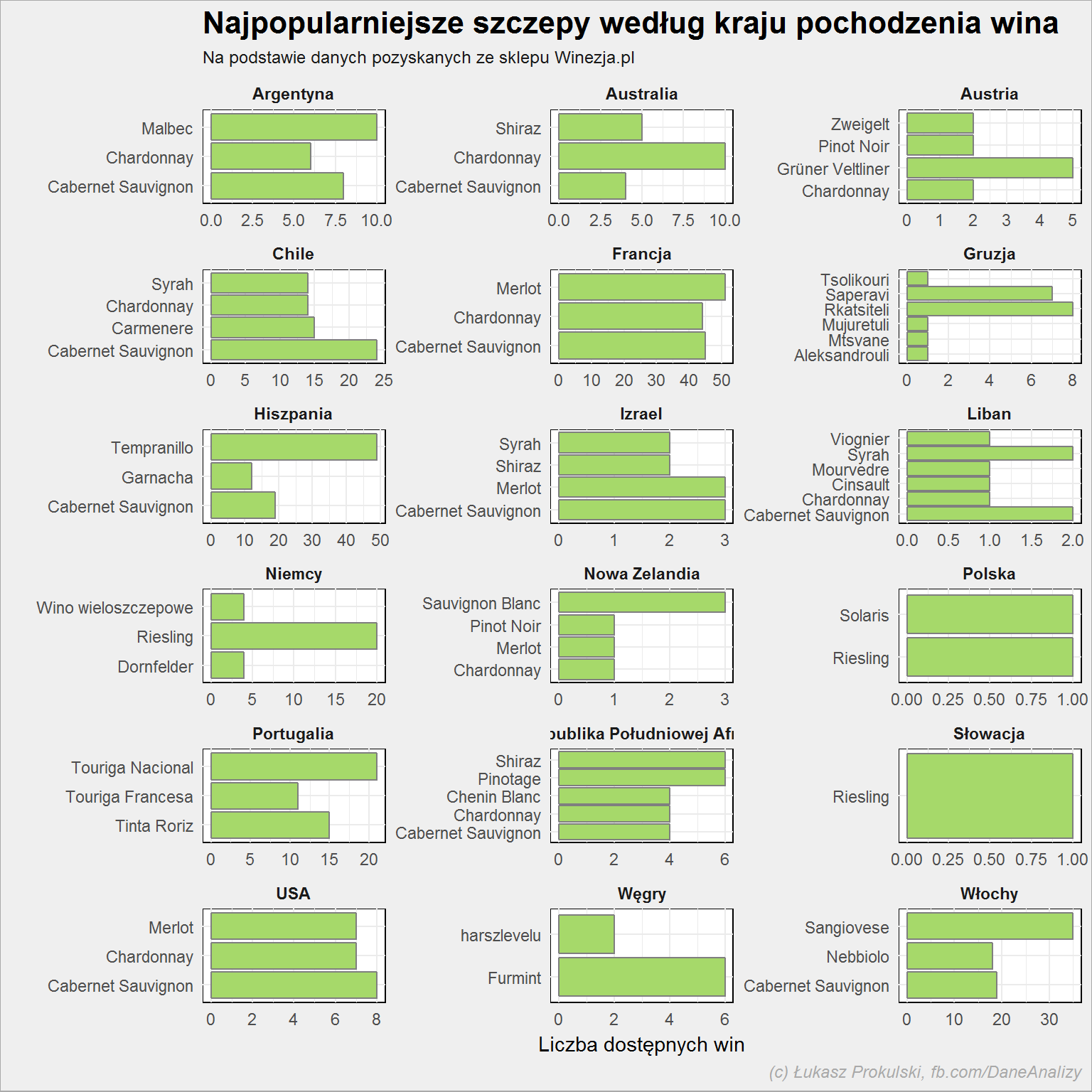
Cabernet Sauvignon czy Merlot to najpopularniejsze szczepy, jak widać występują w wielu krajach. Podobnie jest z Syrah czy Shiraz. Ale są unikaty – Furmint z Węgier, niemiecki (i trochę też polski albo słowacki) Riesling. Gruzja, Portugalia, Hiszpania i Włochy mają swoje lokalne szczepy.
Wino z którego szczepu winogron jest najlepsze według ekspertów?
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
lista_win %>% select(expert_rating, szczep) %>% separate(szczep, paste0("Szczep", 1:8), sep = ",") %>% gather(dummy, Szczep, -expert_rating) %>% filter(!is.na(Szczep)) %>% select(-dummy) %>% rowwise() %>% mutate(Szczep = str_trim(str_replace(Szczep,"\\(.*\\)", ""))) %>% ungroup() %>% group_by(Szczep) %>% summarise(ocena = mean(expert_rating, na.rm = T)) %>% ungroup() %>% arrange(ocena) %>% top_n(10, ocena) %>% mutate(Szczep = factor(Szczep, level=Szczep)) %>% ggplot() + geom_point(aes(Szczep, ocena), color = "#d7191c", size = 4) + geom_text(aes(Szczep, ocena, label = round(ocena, 1)), color = "gray50", vjust=-1.1) + scale_y_continuous(limits = c(90, 100)) |
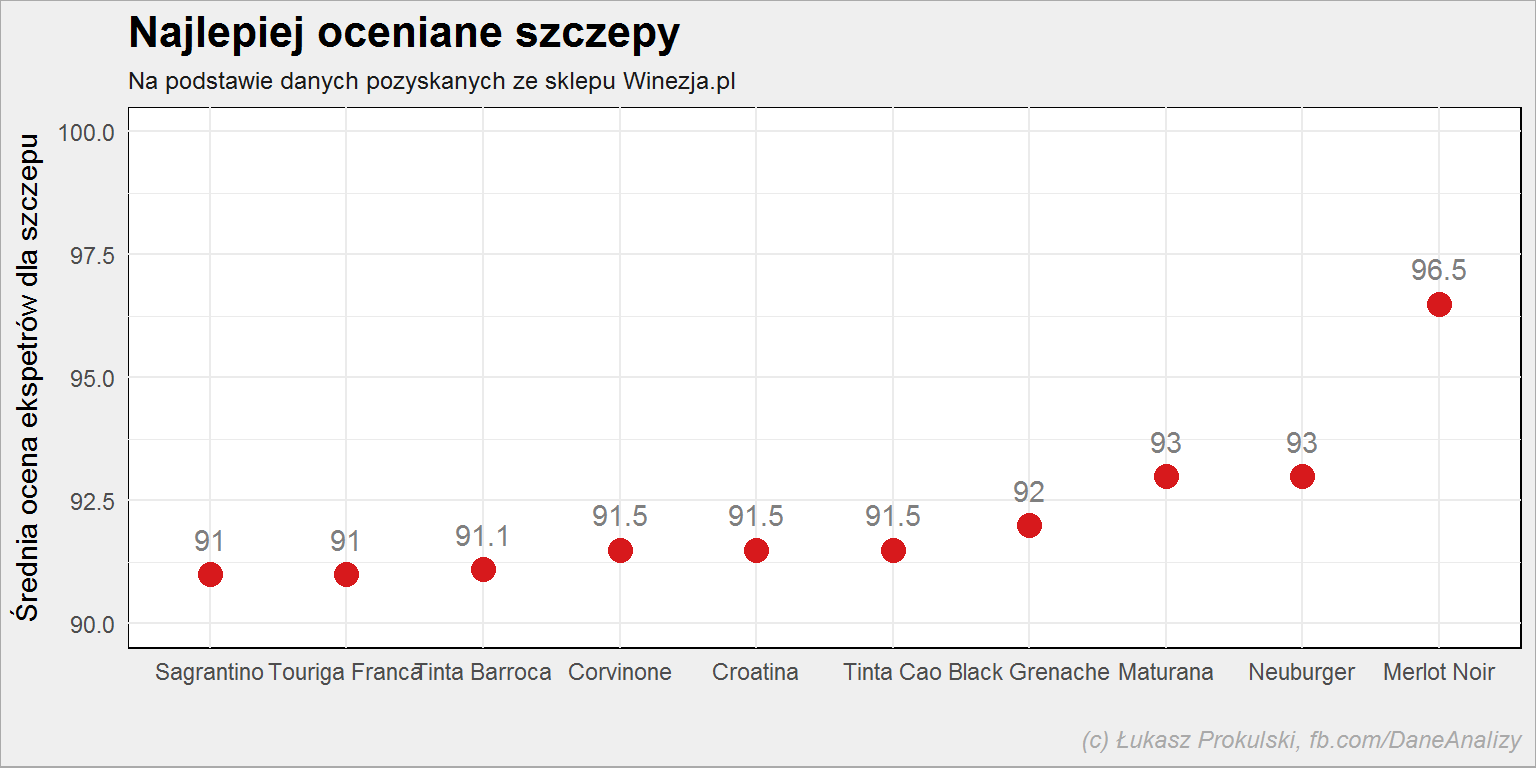
Merlot Noir i dwa wina pochodzące (częściowo) z tego szczepu:
|
1 |
lista_win %>% filter(grepl("Merlot Noir", szczep)) %>% select(nazwa, szczep, expert_rating) |
| Nazwa | Szczep | Ocena |
|---|---|---|
| Château Haut-Brion Pessac-Leognan Rouge AOC 2010 | Cabernet Sauvignon (57%), Merlot Noir (23%), Cabernet Franc (20%) |
98 |
| Château La Mission Haut-Brion Pessac-Léognan Rouge AOC 2010 | Cabernet Sauvignon (62%), Merlot Noir (37%), Cabernet Franc (1%) |
95 |
Oba są czerwonymi winami wytrawnymi z Francji, z rocznika 2010. Château Haut-Brion Pessac-Leognan Rouge AOC 2010 jest najlepiej ocenianym winem w całej Winezji.
Widzieliśmy, że szczep ma wpływ na ocenę, co za tym idzie pewnie też na cenę:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
lista_win %>% filter(!is.na(cena), !is.na(szczep)) %>% select(cena, szczep) %>% separate(szczep, paste0("Szczep", 1:8), sep = ",") %>% gather(dummy, Szczep, -cena) %>% filter(!is.na(Szczep)) %>% select(-dummy) %>% rowwise() %>% mutate(Szczep = str_trim(str_replace(Szczep,"\\(.*\\)", ""))) %>% ungroup() %>% group_by(Szczep) %>% summarise(m_cena = mean(cena)) %>% ungroup() %>% top_n(25, m_cena) %>% arrange(m_cena) %>% mutate(Szczep = factor(Szczep, levels = Szczep)) %>% ggplot() + geom_col(aes(Szczep, m_cena), color = "gray50", fill = "#a6d96a") + coord_flip() |
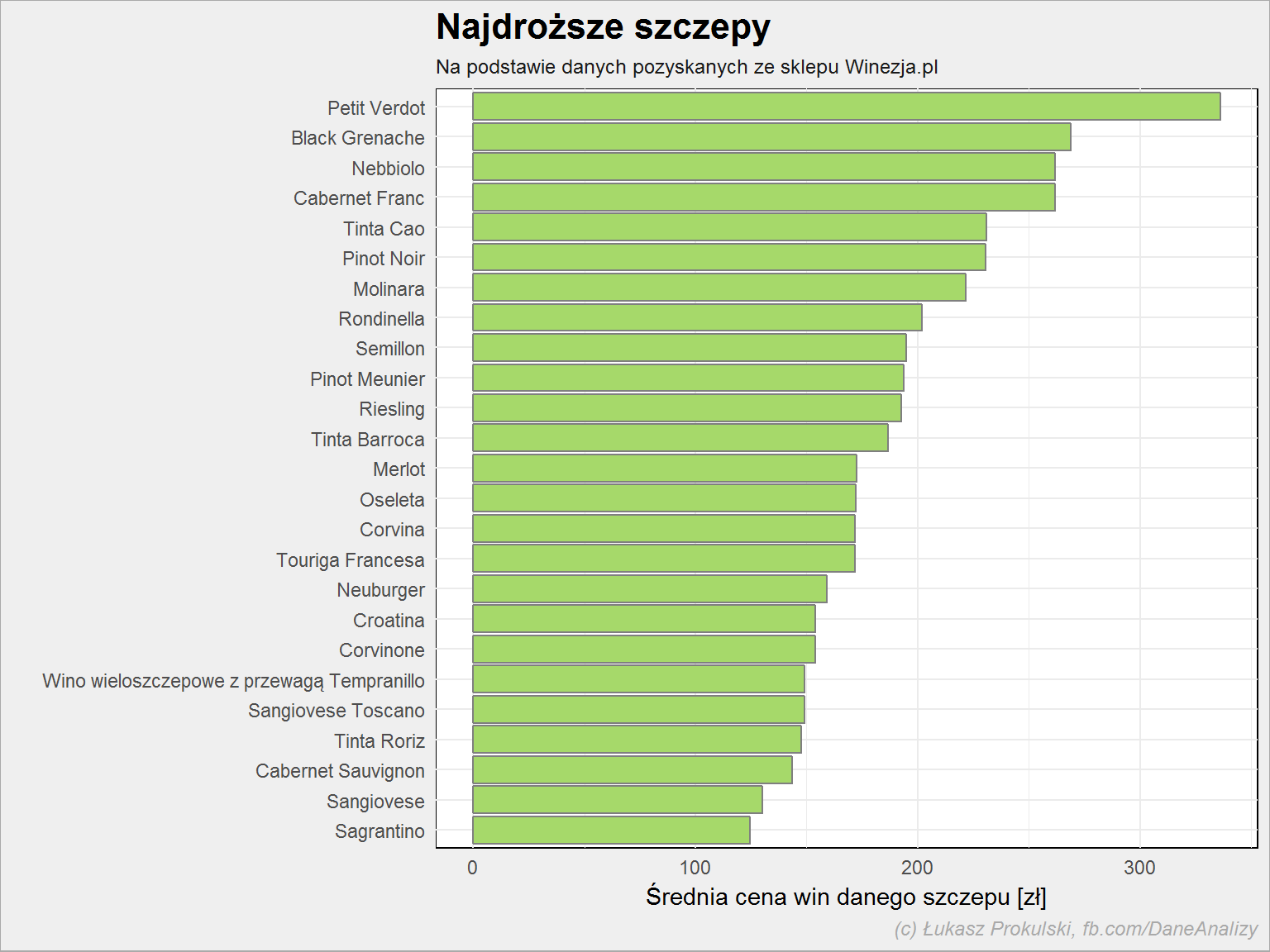
Najdroższym winem ze szczepem Petit Verdot (też w mieszance) jest francuskie czerwone wytrawne Le Clarence de Haut-Brion Pessac-Leognan Rouge AOC 2011 – 999 zł za butelkę.
Mając informację o szczepach i kraju pochodzenia możemy sprawdzić czy szczepy są ograniczone terytorialnie. Widzieliśmy to już wyżej (wykres z najpopularniejszymi szczepami w danym kraju), ale zbudujmy z tych informacji graf, który pokaże nam połączenia:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
library(igraph) graf_df <- lista_win %>% select(kraj, szczep) %>% separate(szczep, paste0("Szczep", 1:8), sep = ",") %>% gather(dummy, Szczep, -kraj) %>% filter(!is.na(Szczep)) %>% select(-dummy) %>% rowwise() %>% mutate(Szczep = str_trim(str_replace(Szczep,"\\(.*\\)", ""))) %>% ungroup() %>% count(kraj, Szczep) %>% ungroup() %>% filter(n >= quantile(n, 0.75)) graf <- graph_from_data_frame(graf_df) E(graf)$width <- graf_df$n com <- cluster_walktrap(graf, weights = E(graf)$width) V(graf)$color <- com$membership+1 graf_lay <- layout_with_fr(graf, weights = E(graf)$width) plot(graf, vertex.label = V(graf)$name, vertex.label.color = "black", vertex.label.cex = 0.8, vertex.label.dist = 0.2, vertex.size = 3, edge.arrow.size = 1, edge.arrow.width = NA, edge.width = 8*E(graf)$width/max(E(graf)$width), edge.curved = TRUE, layout = graf_lay, mark.groups = com) |
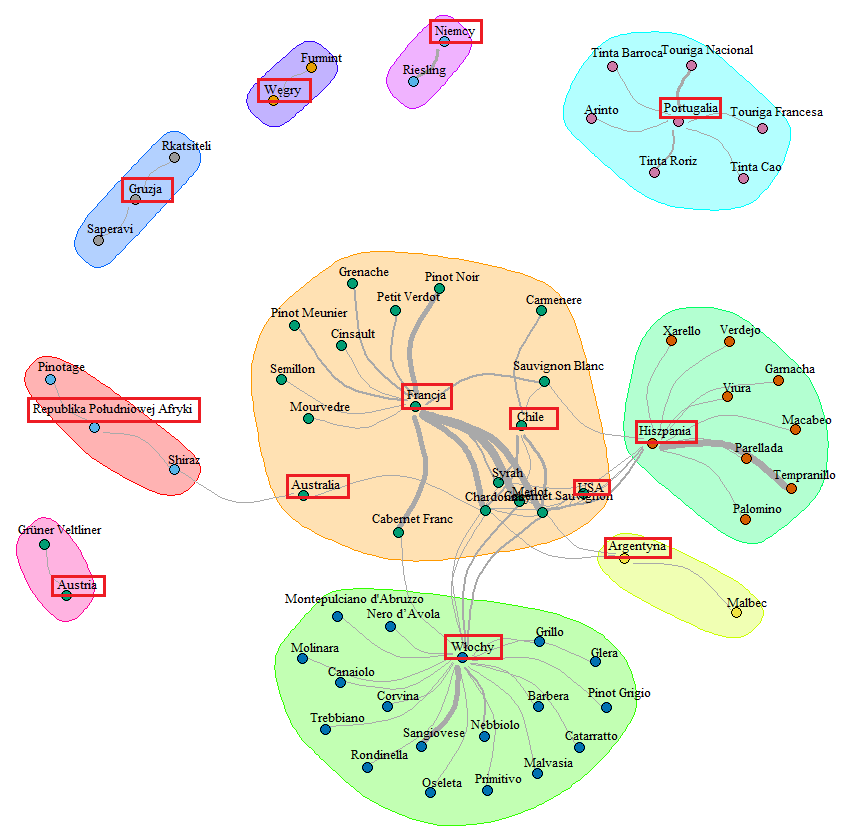
Wzięliśmy pod uwagę tylko górną 1/4 najpopularniejszych szczepów. Przygotowaliśmy grupy poszczególnych szczepów i widać wyraźnie, że istnieje podział terytorialny. Jakiś enolog zapewne mógłby opowiadać o tym godzinami. Jako laik widzę po prostu różnice w klimacie i ukształtowaniu terenu (góry, dostęp do morza).
Czas na najciekawszą sprawę – wybór dobrego i taniego. Wiadomo przecież, że dobre wino jest dobre, bo jest tanie i dobre.
Tylko jak wybrać to najlepsze (według tak założonych kryteriów)?
Najpierw wybierzmy najlepsze z najtańszych, na przykład takie standardowe czerwone półwytrawne:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
tanie_dobre <- lista_win %>% filter(!is.na(expert_rating), !is.na(smak), !is.na(cena), pojemnosc == 0.75) %>% group_by(smak, kolor) %>% top_n(-25, cena) %>% # 25 najtańszych top_n(5, expert_rating) %>% # 5 najlepszych ungroup() %>% select(smak, kolor, nazwa, kraj, cena, expert_rating) %>% arrange(smak, kolor, desc(cena), expert_rating) # najpopularniejsze wina tanie_dobre %>% filter(smak == "Półwytrawne", kolor == "Czerwone") %>% arrange(cena, desc(expert_rating)) %>% select(nazwa, kraj, cena, expert_rating) |
| Nazwa | Kraj | Cena | Ocena |
|---|---|---|---|
| Les Grands Chemins Carignan | Francja | 29.99 | 84 |
| Parthenium Nero D’Avola I.G.P. | Włochy | 29.99 | 81 |
| Fiuza 3 Castas Touriga Nacional Semi Dry Red | Portugalia | 34.99 | 84 |
| Sachino Red | Gruzja | 39.99 | 81 |
| Almarosa Primitivo Puglia I.G.T. | Włochy | 44.99 | 82 |
Teraz odwróćmy kolejność: najtańsze białe półsłodkie z najlepszych:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
dobre_tanie <- lista_win %>% filter(!is.na(expert_rating), !is.na(smak), !is.na(cena), pojemnosc == 0.75) %>% group_by(smak, kolor) %>% top_n(25, expert_rating) %>% # 25 najlepszych top_n(-5, cena) %>% # 5 najtańszych ungroup() %>% select(smak, kolor, nazwa, kraj, cena, expert_rating) %>% arrange(smak, kolor, expert_rating, desc(cena)) dobre_tanie %>% filter(smak == "Półsłodkie", kolor == "Białe") %>% arrange(desc(expert_rating), cena) %>% select(nazwa, kraj, cena, expert_rating) |
| Nazwa | Kraj | Cena | Ocena |
|---|---|---|---|
| Franz Reh & Sohn Piesporter Michelsberg | Niemcy | 29.99 | 83 |
| Cava Rigol Semi Seco | Hiszpania | 29.99 | 82 |
| Villa Rosale Chardonnay Pinot Bianco I.G.T. | Włochy | 24.99 | 81 |
| Wine Moments Müller-Thurgau Leiblich | Niemcy | 24.99 | 80 |
| Kumala Cape Classics White | Republika Południowej Afryki | 24.99 | 79 |
| Liebfraumilch Johannes Egberts | Niemcy | 16.59 | 78 |
A co dostaniemy łącząc oba zbiory i wybierając te z najniższą ceną?
|
1 2 3 4 |
intersect(tanie_dobre, dobre_tanie) %>% group_by(smak, kolor) %>% filter(cena == min(cena)) %>% ungroup() |
| Smak | Kolor | Nazwa | Kraj | Cena | Ocena |
|---|---|---|---|---|---|
| Półsłodkie | Czerwone | Vinha Maria Medium Sweet Red | Portugalia | 27.99 | 83 |
| Półsłodkie | Różowe | Wine Moments Dornfelder Lieblich Rose | Niemcy | 24.99 | 79 |
| Półsłodkie | Różowe | Villa Rosale Zinfandel I.G.T. | Włochy | 24.99 | 80 |
| Półwytrawne | Czerwone | Parthenium Nero D’Avola I.G.P. | Włochy | 29.99 | 81 |
| Półwytrawne | Czerwone | Les Grands Chemins Carignan | Francja | 29.99 | 84 |
| Półwytrawne | Różowe | Les Grands Chemins Cinsault Rose | Francja | 29.99 | 83 |
| Wytrawne | Inne | Alma Azul Blue Chardonnay Sparkling | Hiszpania | 59.99 | 80 |
Czy to dobra metoda? Niekoniecznie. A może po prostu kierować się wskaźnikiem jakości do ceny? Wybierzmy więc według tej miary wina przy dodatkowym założeniu, że szukamy tylko z tych lepszych połówek ceny (niższa cena) i jakości (wyższa ocena ekspertów):
|
1 2 3 4 5 6 7 8 9 10 11 12 |
lista_win %>% filter(!is.na(smak), pojemnosc == 0.75) %>% group_by(smak, kolor) %>% # chcemy te z górnej połowy jakości i dolnej połowy ceny filter(expert_rating >= median(expert_rating, na.rm = TRUE), cena <= median(cena, na.rm = TRUE)) %>% mutate(jakosc_cena = expert_rating / cena) %>% top_n(1, jakosc_cena) %>% ungroup() %>% select(smak, kolor, nazwa, kraj, cena, expert_rating, jakosc_cena) %>% arrange(smak, kolor, desc(jakosc_cena)) %>% mutate(jakosc_cena = round(jakosc_cena, 2)) |
| Smak | Kolor | Nazwa | Kraj | Cena | Ocena | Jakość/Cena |
|---|---|---|---|---|---|---|
| Półsłodkie | Białe | Franz Reh & Sohn Piesporter Michelsberg | Niemcy | 29.99 | 83 | 2.77 |
| Półsłodkie | Czerwone | Vinha Maria Medium Sweet Red | Portugalia | 27.99 | 83 | 2.97 |
| Półsłodkie | Różowe | Villa Rosale Zinfandel I.G.T. | Włochy | 24.99 | 80 | 3.20 |
| Słodkie | Białe | Osborne Sherry Medium Golden | Hiszpania | 49.99 | 84 | 1.68 |
| Półwytrawne | Białe | Senorío De Orgaz Semi Seco | Hiszpania | 27.99 | 83 | 2.97 |
| Półwytrawne | Czerwone | Les Grands Chemins Carignan | Francja | 29.99 | 84 | 2.80 |
| Półwytrawne | Różowe | Les Grands Chemins Cinsault Rose | Francja | 29.99 | 83 | 2.77 |
| Wytrawne | Białe | Senorío De Orgaz Brut | Hiszpania | 27.99 | 84 | 3.00 |
| Wytrawne | Czerwone | Bajoz Crianza Toro | Hiszpania | 34.99 | 86 | 2.46 |
| Wytrawne | Różowe | Chivite Gran Feudo Rosado Navarra D.O. | Hiszpania | 39.99 | 85 | 2.13 |
| Wytrawne | Inne | Alma Azul Blue Chardonnay Sparkling | Hiszpania | 59.99 | 80 | 1.33 |
Zobaczmy czy oferta jest w pewnym sensie zbalansowana – czy mamy tyle samo win zbyt drogich w porównaniu do ich jakości co zbyt tanich? Jak wygląda rozkład jakości do ceny? Teoretycznie rozkłady powinny być symetryczne.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
lista_win %>% filter(!is.na(smak), pojemnosc == 0.75, kolor != "Inne", !is.na(expert_rating), !is.na(cena)) %>% group_by(smak, kolor) %>% mutate(jakosc_cena = expert_rating / cena) %>% mutate(median_jakosc_cena = median(jakosc_cena, na.rm = TRUE)) %>% ungroup() %>% ggplot() + geom_density(aes(jakosc_cena), color = "gray50", fill = "#a6d96a") + geom_vline(aes(xintercept = median_jakosc_cena), color = "red") + facet_grid(smak~kolor, scales = "free") + labs(title = "Rozkład jakości do ceny dla różnych gatunków wina", subtitle = "Na podstawie danych pozyskanych ze sklepu Winezja.pl", x = "Stosunek jakości do ceny", y = "", caption = "(c) Łukasz Prokulski, fb.com/DaneAnalizy") |
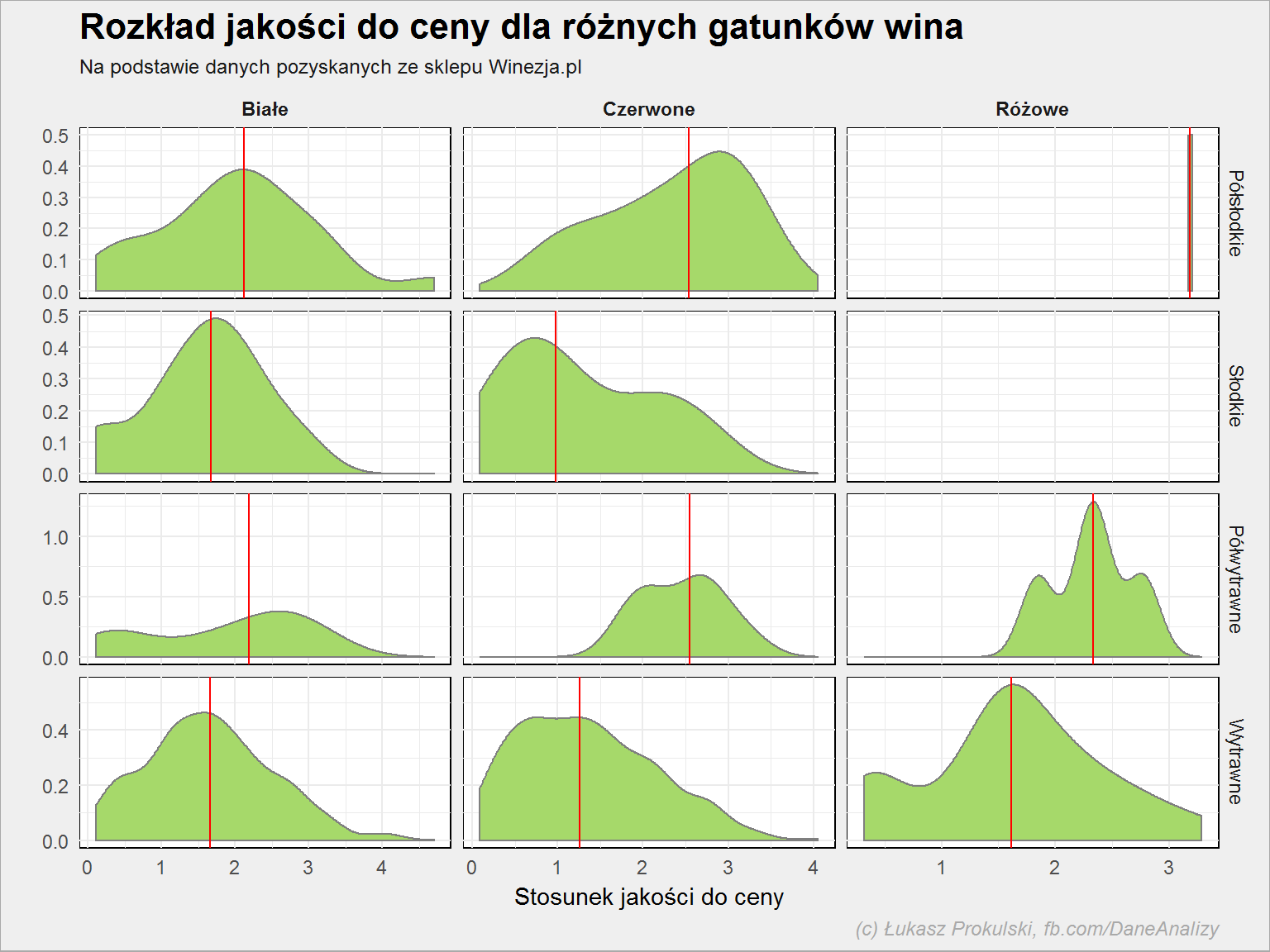
Czerwona linia to mediana.
Niestety w danych nie znajdziemy informacji o różnych wskaźnikach jakimi zapewne można opomiarować wino – takie dane znaleźć można na UCI, w paczce Wine Data Set. Gdybyśmy takie dane posiadali zabawa byłaby jeszcze lepsza. Można by przygotować jakieś modele regresyjne albo klasyfikujące. Tutaj oceny cząstkowe (aromat, gładkość itd.), ceny czy oceny ekspertów są zbyt zbliżone, aby cokolwiek na ich podstawie wnioskować czy przewidywać. Tak czy inaczej – mam nadzieję, że się podobało, a i o winie czegoś się dowiedzieliście.
Na koniec chciałbym zaznaczyć, że sklep Winezja.pl w żaden sposób nie sponsorował tego wpisu (a szkoda – byłoby łatwiej z kieliszkiem w dłoni ;-). Co więcej – był (może nadal jest? możecie im donieść…) nieświadomy całej akcji i analizy. Trafiło na ten sklep z Google – był to pierwszy sklep, który na stronie prezentował interesujące mnie dane. Być może odkrywam jakieś tajemnice handlowe sklepu – nie wiem, na pewno nie robię tego rozmyślnie.
Inspiracją dla wpisu: Analyzing 1000+ Greek Wines With Python.
„Czas na najciekawszą sprawę – wybór dobrego i taniego. Wiadomo przecież, że dobre wino jest dobre, bo jest tanie i dobre.” – chyba malutki błąd – powinno być „tanie wino jest dobre (…)”
Jest tak jak być powinno. Z rozmysłem. :)
Chciałem zauważyć, że ocena 4.9 jednego wina, która została uśredniona z 4 głosów jest zupełnie inną oceną niż ocena 4.5 (chociażby), która została uśredniona z 50 głosów. Dlatego wskaźnik oceny, który jest tu brany jest dość niemiarodajny.
Gdyby zastosować chociażby takie podejście: http://www.evanmiller.org/how-not-to-sort-by-average-rating.html – sortowanie według oceny byłoby znacznie bardziej wymowne.
Nie spodziewałem się takiego wpisu, tym bardziej, że szykuję wesele i właśnie szukałem informacji o winach :) Czy istnieje jakaś możliwość by mógł Pan sprawdzić jak by to wyglądało z wykorzystaniem tego binoma?
Ok, zauważyłem, że bierzesz pod uwagę opinie eksperta, a nie opinie wystawione przez ludzi, to zmienia zupełnie mój tok rozumowania :)
To jak już lubię sobie popisać, to w ostatnim wykresie rozumiem, że wartość x to jest jakosc_cena, a czym w takim razie jest wartość y? Na nie wiem skąd jest wyliczana, żeby zrozumieć ten wykres.
Czytając dokumentację medoty geom_density() (http://ggplot2.tidyverse.org/reference/geom_density.html) wydaje mi się, że ta wartość to jest wskaźnik „gęstości występowania takiego jakosc_cena”. Czyli biorąc na tapet wina białe słodkie: najwięcej można spotkać takich, których jakość/cena jest równa mniej więcej 1.7~1.8
Dobrze kombinuję? :)
Dokładnie tak.
Zgadza się – to uśrednianie nie miałoby sensu. Ale jak zam zauważyłeś to ocena ekspertów. A poza tym – jak zawsze w moich wpisach – analiza zrobiona dla zabawy, w kilka godzin.
W kilka godzin? Wow. Czy to wliczając napisanie skryptu ściągającego dane że sklepu?
Zapewne tak. Zwykle cały proces powstawania wpisu dałoby się zamknąć w okolicach 20 godzin. Kod idzie szybko (analiza jest wynikiem zabawy danymi i to co uznaję za ciekawe zostaje we wpisie – dlatego często powtarzają się fragmenty tego samego kodu, zupełnie bez sensu powtarzane są obliczenia typu filtrowanie czy grupowanie), opisywanie długo. Najdłużej zbieranie danych (scrapping czy jak w przypadku sieci neuronowych trening sieci).